Cho (O) có 2 đường kính AB & CD ⊥ với nhau. Đ' E ϵ OC ( E # O, C ). nối AE cắt (O) tại M
a, CMR : AC2 = AE . AM
b, xác định vị trí của E trên OC để MA = 2MB
WO
Những câu hỏi liên quan
1. Cho đường tròn (O ; 10cm). Dây AB = 16cm. Tiếp tuyến tại A của đường tròn cắt đường kính vuông góc với AB tại C. Hãy tính khoảng cách từ tâm O đến dây AB.
2. Cho đường tròn (O) có đường kính AB. Vẽ dây AC của đường tròn
a) So sánh AB và BC
b) Tam giác ABC là tam giác gì. Vì sao?
c) Từ O kẻ OM // BC (điểm M thuộc AC) Chứng minh AM = MC
Câu 1:
Gọi giao điểm của OC với AB là H
Vì OC\(\perp\)AB nên OH\(\perp\)AB tại H
=>OH là khoảng cách từ O xuống dây AB
Ta có: ΔOAB cân tại O
mà OH là đường cao
nên H là trung điểm của AB
=>HA=HB=AB/2=8(cm)
ΔOHA vuông tại H
=>\(OH^2+HA^2=OA^2\)
=>\(OH^2=10^2-8^2=36\)
=>\(OH=\sqrt{36}=6\left(cm\right)\)
Câu 2:
a: Xét (O) có
AB là đường kính
BC là dây
Do đó: AB>BC
b: Xét (O) có
ΔCAB nội tiếp
AB là đường kính
Do đó: ΔCAB vuông tại C
c: Xét ΔACB có
O là trung điểm của AB
OM//CB
Do đó: M là trung điểm của AC
Đúng 0
Bình luận (0)
Cho nửa đường tròn tâm O có đường kính AB/2 RCho nửa đường tròn tâm O có đường kính AB 2R. Kẻ hai tiếp tuyến Ax, By của nửa đường tròn (O) tại A và B (Ax, By và nửa đường tròn thuộc cùng một nửa mặt phẳng có bờ là đường thẳng AB). Qua điểm M thuộc nửa đường tròn (M khác A và B), kẻ tiếp tuyến với nửa đường tròn, cắt tia Ax và By theo thứ tự tại C và D.a, CM : góc COD 90ob, CM : CD AC + BDc)Cm AC.BDABmu 2d)CM OC//BMe)CM AB la tiep tuyen (oCD/2)k)CM MN vuong goc ABh)xac dinh vi tri diem M de c...
Đọc tiếp
Cho nửa đường tròn tâm O có đường kính AB/2 = R
Cho nửa đường tròn tâm O có đường kính AB = 2R. Kẻ hai tiếp tuyến Ax, By của nửa đường tròn (O) tại A và B (Ax, By và nửa đường tròn thuộc cùng một nửa mặt phẳng có bờ là đường thẳng AB). Qua điểm M thuộc nửa đường tròn (M khác A và B), kẻ tiếp tuyến với nửa đường tròn, cắt tia Ax và By theo thứ tự tại C và D.
a, CM : góc COD = 90o
b, CM : CD = AC + BD
c)Cm AC.BD=ABmu 2
d)CM OC//BM
e)CM AB la tiep tuyen (o'CD/2)
k)CM MN vuong goc AB
h)xac dinh vi tri diem M de chu vi ACDB co GTNN
Cho hình trụ có các đường tròn đáy là (O) và (O’), bán kính đáy bằng 1 chiều cao bằng 2. AB, CD lần lượt là đường kính của đường tròn đáy (O) và (O’) sao cho AB vuông góc CD. Tính cosin góc giữa hai đường thẳng AC và BD. A.
2
3
B.
1
2
C.
3
2
D.
1
3
Đọc tiếp
Cho hình trụ có các đường tròn đáy là (O) và (O’), bán kính đáy bằng 1 chiều cao bằng 2. AB, CD lần lượt là đường kính của đường tròn đáy (O) và (O’) sao cho AB vuông góc CD. Tính cosin góc giữa hai đường thẳng AC và BD.
A. 2 3
B. 1 2
C. 3 2
D. 1 3
Cho hình trụ có các đường tròn đáy là (O) và (O’), bán kính đáy bằng 1 chiều cao bằng 2. AB, CD lần lượt là đường kính của đường tròn đáy (O) và (O’) sao cho AB vuông góc CD. Tính cosin góc giữa hai đường thẳng AC và BD. A.
1
2
B.
3
2
C.
2
3
D.
1
3
Đọc tiếp
Cho hình trụ có các đường tròn đáy là (O) và (O’), bán kính đáy bằng 1 chiều cao bằng 2. AB, CD lần lượt là đường kính của đường tròn đáy (O) và (O’) sao cho AB vuông góc CD. Tính cosin góc giữa hai đường thẳng AC và BD.
A. 1 2
B. 3 2
C. 2 3
D. 1 3
Cho tam giác ABC có A >90o. Vẽ đường tròn (O) đường kính AB và đường tròn (O') đường kính AC. Đường thẳng AB cắt đường tròn (O') tại điểm thứ 2 là D,dường thẳng AC cắt đường tròn (O) tại điểm thứ 2 là E
a)Chứng minh bốn điểm B,C,D,E cùng nằm trên 1 đường tròn
góc AEB=1/2*180=90 độ
góc CDA=1/2*180=90 độ
góc CEB=góc CDB
=>CDEB nội tiếp
Đúng 0
Bình luận (0)
Cho nửa đường tròn tâm O, đường kính AB. 2 điểm C, D thuộc nửa đường tròn tâm O, đường kính AB. Biết BD= 6 cm. Tính bán kính đường tròn
Cho đường tròn (O), đường kính AB, điểm C nằm giữa A và O. Vẽ đường tròn (O’) có đường kính CB. Hai đường tròn (O) và (O’) có vị trí tương đối như thế nào đối với nhau?
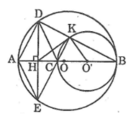
Vì O, O’ và B thẳng hàng nên: O’B < OB => O’ nằm giữa O và B
Ta có: OO’ = OB - O’B
Vậy đường tròn (O’) tiếp xúc với đường tròn (O) tại B
Đúng 0
Bình luận (0)
Cho nửa đường tròn (O) đường kính AB. Trên nửa đường tròn lấy B,C sao cho AB=BC= 2√5 cm, CD=6cm. Tính bán kính của (O)
khong duoc dat ten la ab ma phai la du ma
Đúng 0
Bình luận (0)
https://olm.vn/hoi-dap/detail/66015664055.html bạn vào đây tham khảo nha
Đúng 0
Bình luận (0)
Cho đường tròn (O), đường kính AB, điểm C nằm giữa A và O. Vẽ đường tròn (O’) có đường kính CB. Chứng minh rằng HK là tiếp tuyến của đường tròn (O’)
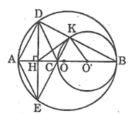
Tam giác DEK vuông tại K có KH là trung tuyến thuộc cạnh huyền DE nên: HK = HE = (1/2).DE (tính chất tam giác vuông)
Suy ra tam giác EHK cân tại H
Đúng 0
Bình luận (0)
Cho đường tròn (O), đường kính AB, điểm C nằm giữa A và O. Vẽ đường tròn (O') có đường kính CB
d) Chứng minh HK là tiếp tuyến của đường tròn (O')
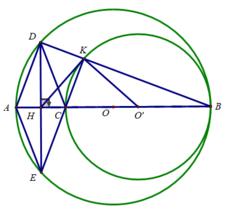
d) Xét tam giác DEK vuông tại K có KH là trung tuyến nên KH = HE
ΔKHE có KH = HE ⇒ ΔKHE cân tại H
⇒ ∠(HKE ) = ∠(KEH)
Lại có ΔO'CK cân tại O' ⇒ ∠(O'CK) = (O'KC)
⇒ ∠(HKE ) + ∠(O'KC) = ∠(KEH) + ∠(O'CK)
⇔ ∠(O'KH) = ∠(KEH) + ∠(O'CK)
Mặt khác ∠(O'CK) = ∠(HCE) (đối đỉnh)
ΔHEC vuông tại H nên ∠(KEH) + ∠(HCE) = 90o ⇒ ∠(KEH) + ∠(O'CK) = 90 0
Hay ∠(O'KH) = 90 0
⇒ KH là tiếp tuyến của (O')
Đúng 0
Bình luận (0)