chứng minh rằng trong 1 tam giác cân, trung điểm của cạnh đáy đều cách đều hai cạnh bên
chứng minh rằng trong 1 tam giác cân, trung điểm của cạnh đáy đều cách đều hai cạnh bên
Giả sử cho tam giác ABC cân tại A, M là trung điểm của BC; từ M kẻ MD,ME lần lượt vuông góc với AB,AC tại D,E.
Bây giờ ta cần chứng minh MD=ME
Bài làm:
Vì M là trung điểm của BC
=> AM là trung tuyến của tam giác ABC; mà tam giác ABC cân tại A
=> AM đồng thời là đường phân giác của tam giác ABC
=> \(\widehat{BAM}=\widehat{MAC}\)(hoặc bạn có thể chứng minh \(\Delta AMB=\Delta AMC\left(c.c.c\right)\))
\(\Delta AMD=\Delta AME\left(c.h-g.n\right)\)
vì: \(\hept{\begin{cases}AMchung\\\widehat{BAM}=\widehat{MAC}\left(cmt\right)\end{cases}}\)
=> MD=ME
=> Trung điểm của canh đáy của tam giác cân cách đều 2 canh bên của tam giác
=> đpcm
Học tốt!!!!
đặt tam giác ABC cân tại A và có M là trung điểm của BC, tự vẽ hình nha
xét tam giác ABM và tam giác ACM có
AB=AC(gt)
ABC=ACB(gt)
BM=CM(gt)
=> tam giác ABM= tam giác ACM(cgc)
=>BAM=CAM( hai góc tương ứng)
=> AM là phân giác của BAC=> M thuộc tia phân giác của BAC
=> M cách đều hai cạnh bên của tam giác
Chứng minh trong tam giác cân, trung điểm của cạnh đáy cách đều hai cạnh bên
a) Chứng minh trong tam giác ABC cân tại A, đường trung trực của cạnh BC là đường cao và cũng là đường phân giác xuất phát từ đỉnh A của tam giác đó.
b) Chứng minh rằng trong tam giác đều, điểm cách đều ba đỉnh cũng cách đều ba cạnh của tam giác.
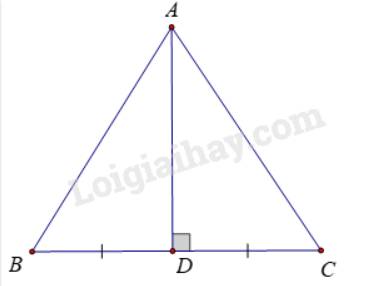
a) Kẻ đường trung trực của đoạn thẳng BC, cắt BC tại D
Ta có: Tam giác ABC cân nên AB = AC
\( \Rightarrow A\)thuộc đường trung trực của cạnh BC (t/c)
\( \Rightarrow AD\)là đường trung trực của BC.
Xét \(\Delta ABD\)và \(\Delta ACD\)có:
AB = AC (gt)
BD = CD (gt)
AD: cạnh chung
\( \Rightarrow \Delta ABD = \Delta ACD\left( {c - c - c} \right)\)
\( \Rightarrow \widehat {BAD} = \widehat {CAD}\)
\( \Rightarrow \)AD là tia phân giác góc BAC.
Vậy tam giác ABC cân tại A, đường trung trực của cạnh BC là đường cao và cũng là đường phân giác xuất phát từ đỉnh A của tam giác đó.
b)
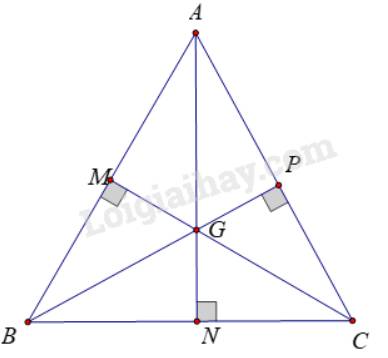
Ta có: Điểm cách đều ba đỉnh của tam giác là giao điểm ba đường trung trực của tam giác đó.
Tam giác ABC đều nên AB = BC = CA
Tam giác ABC cân tại A có AN là đường trung tuyến
\( \Rightarrow \) AN là đường phân giác xuất phát từ đỉnh A (cm ở ý a)
Tương tự: BP, CM lần lượt là đường phân giác xuất phát từ B và C của tam giác ABC
Mà AN cắt BP tại G
\( \Rightarrow G\) là giao điểm ba đường phân giác của tam giác ABC
\( \Rightarrow G\) cách đều ba cạnh của tam giác ABC (Tính chất
chứng minh rằng trong tam giác cân tổng các khoảng cách từ một điểm bất kỳ trên cạnh đáy đến hai cạnh bên không phụ thuộc vào vị trí của điểm đó trên cạnh đáy
Cho hình thang cân ABCD có đáy lớn CD bằng 2 lần cạnh bên BC. Về bên ngoài hình thang dựng các tam giác đều ADF và BCE. G là trung điểm của CD. a) Chứng minh rằng tam giác EGF cân. b) Biết tam giác EFG vuông, AB = a. Tính các góc và các cạnh của hình thang.
Cho hình thang cân ABCD có đáy lớn CD bằng 2 lần cạnh bên BC. Về bên ngoài hình thang dựng
các tam giác đều ADF và BCE. G là trung điểm của CD.
a) Chứng minh rằng tam giác EGF cân.
b) Biết tam giác EFG vuông, AB = a. Tính các góc và các cạnh của hình thang
Cho hình lăng trụ tam giác ABC.A'B'C'có tất cả các cạnh bên và cạnh đáy đều bằng a. Các cạnh bên của lăng trụ tạo với mặt phẳng đáy góc 60 ο và hình chiếu vuông góc của đỉnh A lên mặt phẳng (A'B'C') trùng với trung điểm của cạnh B'C'.
a) Tính khoảng cách giữa hai mặt phẳng đáy của lăng trụ.
b) Chứng minh rằng mặt bên BCC'B' là một hình vuông.
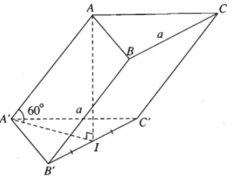
a) Gọi I là trung điểm của cạnh B'C'. Theo giả thiết ta có AI ⊥ (A'B'C') và ∠ A A ′ I = 60 ο . Ta biết rằng hai mặt phẳng (ABC) và (A'B'C') song song với nhau nên khoảng cách giữa hai mặt phẳng chính là khoảng cách AI.
Do đó
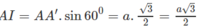
b) 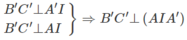
⇒ B′C′ ⊥ AA′
Mà AA′ // BB′ // CC′ nên B’C’ ⊥ BB’
Vậy mặt bên BCC’B’ là một hình vuông vì nó là hình thoi có một góc vuông.
Chứng minh rằng hiệu các khoảng cách từ một điểm nằm trên phần kéo dài của cạnh đáy tam giác cân tại hai cạnh bên bằng chiều cao tương ứng với cạnh bên
c1:
gọi D là điểm trên cạnh đáy kéo dài BC của tam giác cân ABC.(D thuộc tia BC)
H, K là hình chiếu của D trên AB, AC .do tam giác ABC cân tại A suy ra DB là phân giác HDK (1)
gọi CP là đường cao của tam giác ABC.kẻ CQ vuông góc DH (2)
theo (1) và (2) ta suy ra điều phải chứng minh
C2:
từ B kẻ BP vuông góc DK, BH vuông góc AC (3)
từ (1) và (3) suy ra điều phải chứng minh
Hình chóp S.ABC là hình chóp tam giác đều, có cạnh đáy bằng a và cạnh bên bằng a 2 . Một mặt cầu đi qua đỉnh A và tiếp xúc với hai cạnh SB , SC tại trung điểm của mỗi cạnh. Chứng minh rằng mặt cầu đó đi qua trung điểm của AB và AC.
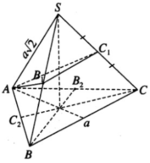
Giả sử mặt cầu đi qua đỉnh A của hình chóp và tiếp xúc với cạnh SB tại B1, tiếp xúc với cạnh SC tại C 1 . Khi đó mặt cầu cắt cạnh AB, AC lần lượt tại các điểm C 2 , B 2 . Mặt phẳng (SAB) cắt mặt cầu đó theo giao tuyến là một đường tròn. Đường tròn này tiếp xúc với SB tại B1 và đi qua A và C 2
Do đó, ta có: BB 1 2 = BA . BC 2
trong đó 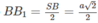
Do đó 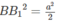
Vậy
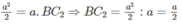
Điều đó chứng tỏ mặt cầu nói trên đi qua trung điểm C 2 của đoạn AB. Lí luận tương tự ta chứng minh được mặt cầu đó đi qua trung điểm B 2 của AC.
Cho hình lăng trụ tam giác ABC.A'B'C' có tất cả các cạnh bên và cạnh đáy đều bằng a. Các cạnh bên của lăng trụ tạo với mặt đáy góc \(60^0\) và hình chiếu vuông góc của đỉnh A lên mặt phẳng (A'B'C') trùng với trung điểm của cạnh B'C'
a) Tính khoảng cách giữa hai mặt phẳng đáy của lăng trụ
b) Chứng minh rằng mặt bên BCC'B' là một hình vuông