cho tam giác ABC có góc A =hai lần góc B chứng minh rằng a2-b2= bc
NL
Những câu hỏi liên quan
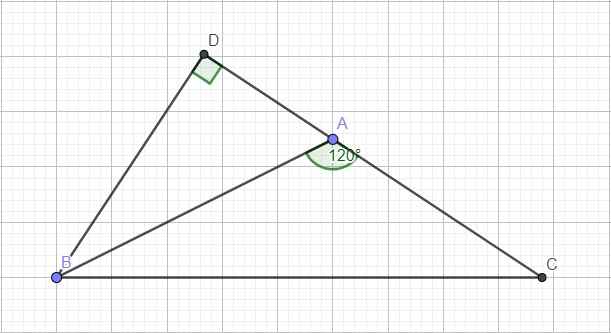
Cho tam giác ABC có góc A = 120 độ, BC = a, AC = b, AB = c. Chứng minh rằng a2 = b2 + c2 + bc ?
Kẻ đường cao BD ứng với AC. Do góc A tù \(\Rightarrow\) D nằm ngoài đoạn thẳng AC hay \(CD=AD+AC\) và \(\widehat{DAB}=180^0-120^0=60^0\)
Áp dụng định lý Pitago:
\(AB^2=BD^2+AD^2\) \(\Rightarrow BD^2=AB^2-AD^2\)
Trong tam giác vuông ABD:
\(cos\widehat{BAD}=\dfrac{AD}{AB}\Rightarrow\dfrac{AD}{AB}=cos60^0=\dfrac{1}{2}\Rightarrow AD=\dfrac{1}{2}AB\)
\(\Rightarrow BD^2=AB^2-\left(\dfrac{1}{2}AB^2\right)=\dfrac{3}{4}AB^2\)
Pitago tam giác BCD:
\(BC^2=BD^2+CD^2=\dfrac{3}{4}AB^2+\left(AD+AC\right)^2\)
\(=\dfrac{3}{4}AB^2+\left(\dfrac{1}{2}AB+AC\right)^2\)
\(=\dfrac{3}{4}AB^2+\dfrac{1}{4}AB^2+AB.AC+AC^2\)
\(=AB^2+AB.AC+AC^2\)
Hay \(a^2=b^2+c^2+bc\)
Đúng 3
Bình luận (0)
Trong tam giác ABC. Chứng minh rằng
a) Góc A nhọn khi và chỉ khi a2 < b2 + c2
b) Góc A tù khi và chỉ khi a2 > b2 + c2
c) Góc A vuông khi và chỉ khi a2 = b2 + c2
Trong tam giác ABC, theo Hệ quả định lý Cô sin ta luôn có :
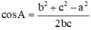
Mà ta có 2.bc > 0 nên cos A luôn cùng dấu với b2 + c2 – a2.
a) Góc A nhọn ⇔ cos A > 0 ⇔ b2 + c2 – a2 > 0 ⇔ a2 < b2 + c2.
b) Góc A tù ⇔ cos A < 0 ⇔ b2 + c2 – a2 < 0 ⇔ a2 > b2 + c2.
c) Góc A vuông ⇔ cos A = 0 ⇔ b2 + c2 – a2 = 0 ⇔ a2 = b2 + c2.
Đúng 0
Bình luận (0)
Bài 4.Cho V ABC cân tại A có góc A 40 độ.Trên cạnh AB lấy điểm D,trên tia đối của tia CA lấy điểm E sao cho BD CE. Kẻ DH và EK cùng vuông góc với đường thẳng BC. (H,K thuộc BC).1) Tính góc B, gócC của tam giác ABC.2)Chứng minh DHEK.3)Gọi M là trung điểm của HK,chứng minh M là trung điểm của DE.Bài 5.Chứng minh rằng nếu a/bb/c thì a2+b2/b2+c2 a/c với b,c khác 0.
Đọc tiếp
Bài 4.Cho V ABC cân tại A có góc A =40 độ.Trên cạnh AB lấy điểm D,trên tia đối của tia CA lấy điểm E sao cho BD= CE. Kẻ DH và EK cùng vuông góc với đường thẳng BC. (H,K thuộc BC).
1) Tính góc B, gócC của tam giác ABC.
2)Chứng minh DH=EK.
3)Gọi M là trung điểm của HK,chứng minh M là trung điểm của DE.
Bài 5.Chứng minh rằng nếu a/b=b/c thì a2+b2/b2+c2= a/c với b,c khác 0.
Cho tam giác ABC có Â = 2 B ^ . Đặt AB = a, AC = b, BC = a. Chứng minh a 2 = b 2 + b c .
Cho tam giác ABC có a 2 = b 2 + c 2 - b c . Số đo của góc A là
A. 135 °
B. 150 °
C. 60 °
D. 120 °
Ta có: a2 = b2 +c2 – bc nên b2 + c2 – a2 = bc
Áp dụng hệ quả định lí cosin trong tam giác ta có:
cos A = b 2 + c 2 − a 2 2. b c = b c 2 b c = 1 2 ⇒ A ^ = 60 °
Chọn C
Đúng 0
Bình luận (0)
Cho tam giác ABC có a2 = b2 + c2 − bc. Góc B bằng bao nhiêu?
A. 1500 B. 1200 C. 600 D. 300
1 Cho tam giác ABC và tam giác A'B'C' có góc A = góc A' BC = B'C' góc B = B' chứng minh rằng tam giác ABC = tam giác A'B'C'
2 Cho tam giác ABC có AB = AC phân giác AD chứng minh rằng AD vuông góc với BC
AI TRA LỜI NHANH GIÚP MÌNH VỚI TvT
2. \(\Delta ABC\)có AB=AC \(\Rightarrow\Delta ABC\)cân.
AD là phân giác \(\Delta ABC\)mà \(\Delta ABC\)cân.
\(\Rightarrow AD\)l là đường trung trực \(\Delta ABC\)..
\(\Rightarrow AD\)là đường cao \(\Delta ABC\)..
\(\Leftrightarrow AD\perp BC\).
Chúc bạn học tốt!
Hình 1 :
Xét \(\Delta ABC\) và \(\Delta A'B'C'\) có : Góc A = Góc A' ( gt ); \(BC=B'C'\left(gt\right)\); Góc B = Góc B' ( gt )
\(\Rightarrow\Delta ABC=\Delta A'B'C\left(ch-gn\right)\)
Hình 2 :
Vì \(\Delta ABC\) có \(AB=AC\Leftrightarrow\Delta ABC\) cân tại A . Vì AD là phân giác góc A
\(\Leftrightarrow\) ^BAD = ^CAD. Xét \(\Delta ABD\) và \(\Delta ACD\) có : \(AB=AC\left(gt\right)\); ^BAD = ^CAD; AD chung.
\(\Rightarrow\Delta ABD=\Delta ACD\left(c.g.c\right)\Leftrightarrow\) ^ADB = ^ADC ( tương ứng ) . Mà ^ADB + ^ADC = 1800 ( kề bù )
\(\Leftrightarrow\) ^ADB = ^ADC = 1800 : 2 = 900 nên suy ra \(AD\perp BC\)
Xem thêm câu trả lời
b1 Cho tam giác ABC có AB = AC. Trên cạnh AB và AC lần lượt lấy hai điểm D và E sao cho AD = AE. Chứng minh rằng góc ADE = góc ABC từ đó suy ra DE // BC.
b2 Cho tam giác ABC đều có ba cạnh bằng 6 cm. Lấy điểm M trên cạnh BC, điểm N trên cạnh AC sao cho MC = NC = 1 cm. Tính chu vi tứ giác ABMN.
B1: \(y=\frac{1}{x^2+\sqrt{x}}\)vì AB=AC=> tam giác ABC cân tại A=> góc B=góc C=> góc B=(180 độ-góc A)/2 (1)
Vì AD=AE=> tam giác ADE cân tại A=> góc ADE=góc AED=> góc ADE=(180 độ-góc A)/2 (2)
Từ (1) và (2)=> góc B=góc ADE
Mà góc B và góc ADE là hai góc đồng vị=> DE//BC
B2: Hình như là 17 cm. Hi hi
Đúng 0
Bình luận (0)
bỏ cái chỗ \(y=\frac{1}{x^2+\sqrt{x}}\) hộ mình cái. mk bấm nhầm
Đúng 0
Bình luận (0)
Cho tam giác ABC có AB = a 5 ; BC = a 3 ; AC = a 2
a, Chứng minh tam giác ABC là tam giác vuông
b, Tính các tỉ số lượng giác của góc B. Từ đó suy ra tỉ số lượng giác của góc A
Cho tam giác ABC có góc B = 2 lần góc C. Chứng minh rằng : AC2 = AB(AB + BC).