7x+7x+7y+7y+97=324
tìm x,y
x^2 - y^2 + 7x - 7y
\(=\left(x-y\right)\left(x+y\right)+7\left(x-y\right)=\left(x+y+7\right)\left(x-y\right)\)
trong mặt phẳng oxy cho phép biến hình f có biểu thức tọa độ x =-3x+4y/5 y = 4x+3y/5 anh cua x+y =0 qua phep bien hinh f la x-7y=0 , 7x-y=0 , 7x+y=0 , x+7y=0
Câu 15. Kết quả phân tích đa thức 6x 2 + 6xy + 7x + 7y thành nhân tử là :
A. (7x+y)(5x+y)
B. ( 3x +5 ) (x+y)
C. ( x+y ) ( 6x + 7)
D. ( 7x +6)( x + y)
Tìm \(x,y\in Z\): \(x^3+7y=y^3+7x\left(x>y>0\right)\)
\(x^3-y^3=7\left(x-y\right)\)
\(\Leftrightarrow\left(x-y\right)\left(x^2+xy+y^2\right)=7\left(x-y\right)\)
\(\Leftrightarrow x^2+xy+y^2=7\)
Nếu \(y\ge2\Rightarrow x\ge3\Rightarrow x^2+xy+y^2>9>7\) (ktm)
\(\Rightarrow y< 2\Rightarrow y=1\)
\(\Rightarrow x^2+x+1=7\Rightarrow x\)
\(\Leftrightarrow x^3-y^3+7y-7x=0\\ \Leftrightarrow\left(x-y\right)\left(x^2+xy+y^2\right)-7\left(x-y\right)=0\\ \Leftrightarrow\left(x-y\right)\left(x^2+xy+y^2-7\right)=0\\ \Leftrightarrow x^2+xy+y^2-7=0\left(x>y\Leftrightarrow x-y>0\right)\\ \Leftrightarrow x^2+xy+y^2=7\)
Vì \(x>y>0\) nên \(x^2< 7\)
Mà \(x\in Z\Leftrightarrow x^2\in\left\{1;4\right\}\)
Với \(x^2=1\Leftrightarrow\left[{}\begin{matrix}x=1\Rightarrow y^2+y-6=0\Rightarrow\left[{}\begin{matrix}y=2\\y=-3\end{matrix}\right.\\x=-1\Rightarrow y^2-y-6=0\Rightarrow\left[{}\begin{matrix}y=-2\\y=3\end{matrix}\right.\end{matrix}\right.\)
Với \(x^2=4\Leftrightarrow\left[{}\begin{matrix}x=2\Rightarrow y^2+2y-3=0\Rightarrow\left[{}\begin{matrix}y=-3\\y=1\end{matrix}\right.\\x=-2\Rightarrow y^2-2y-3=0\Rightarrow\left[{}\begin{matrix}y=-1\\y=3\end{matrix}\right.\end{matrix}\right.\)
Vậy ...(loại mấy TH x,y<0 ra)
x^2*y^2+7x-7y PTNT giùm tôi với
Hệ phương trình x - y = 2 - 7 x + 7 y = 7 có nghiệm là:
A .S = {2;7 }
B .S = ∅
C .S= R
D .S= {2 }
Chọn đáp án B
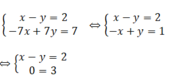
⇒ Hệ phương trình đã cho vô nghiệm ⇒ S = ∅
Cách 2: Ta thấy: 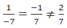 ⇒ Hệ pt vô nghiệm
⇒ Hệ pt vô nghiệm
Tìm x, y thuộc Z biết: x^3+7y=y^3+7x
\(x^3+7y=y^3+7x\)
\(pt\Leftrightarrow x^3-y^3+7y-7x=0\)
\(\Leftrightarrow\left(x^3-y^3\right)-7\left(x-y\right)=0\)
\(\Leftrightarrow\left(x-y\right)\left(x^2+xy+y^2\right)-7\left(x-y\right)=0\)
\(\Leftrightarrow\left(x-y\right)\left(x^2+xy+y^2-7\right)=0\)
x2y-xy2-7x+7y
xy(x - y) - 7(x - y) = (x - y)(xy - 7)