Bài 3. Cho tam giác ABC, M là trung điểm BC. Trên tia đối của MA lấy điểm D sao cho
MD=MA.
a) Chứng minh rằng

AB + AC − BC
2
< AM

b) Chứng minh rằng CD=AB, từ đó suy ra 2AM < AC + AB .

Bài 3. Cho tam giác ABC, M là trung điểm BC. Trên tia đối của MA lấy điểm D sao cho
MD=MA.
a) Chứng minh rằng

AB + AC − BC
2
< AM

b) Chứng minh rằng CD=AB, từ đó suy ra 2AM < AC + AB

Cho tam giác ABC có AC> AB. Trên cạnh AC lấy điểm D sao cho CD = AB. Đường trung trực của AD và đường trung trực của BC cắt nhau ở E. Chứng minh rằng điểm E nằm trên đường tròn ngoại tiếp tam giác ABC 

Trong tam giác ABC, hai đường trung trực của hai cạnh AB và AC cắt nhau tại điểm D nằm trên cạnh BC. Chứng minh rằng:

D là trung điểm của cạnh BC.

Từ một điểm P nằm trên cạnh đáy BC của tam giác ABC vẽ các tia Px, Py song song với các cạnh AB, AC cắt AC tại Q, R. Gọi D là điểm đối xứng với P qua QR. Chứng minh rằng D nằm trên đường tròn ngoại tiếp tam giác ABC

Cho tam giác ABC. Trên tia phân giác của góc B, lấy điểm O nằm trong tam giác ABC sao cho O cách đều hai cạnh AB, AC. Khẳng định nào sau đây sai?

(A) Điểm O nằm trên tia phân giác của góc A.

(B) Điểm O không nằm trên tia phân giác của góc C.

(C) Điểm O cách đều AB, BC.

(D) Điểm O cách đều AB, AC, BC.

Cho tam giác ABC , D và E lần lượt nằm trên các cạnh AB và AC sao cho DE//BC và DE=BC/2 .Đường thẳng qua E song song với AB cắt BC ở M .

a) Chứng minh DE=BM và tam giác ADE=tam giác EMC

b) Chứng minh D là trung điểm cạnh AB.

Cho tam giác ABC cân tại A điển O nằm trong tam giác đó trên cạnh AB lấy điểm D . trên cạnh BC lấy điểm E sao cho OD song song BC . OE song song AC .Chứng Minh rằng tứ giác DOEB là hình thang cân

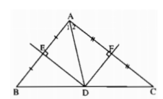
Câu 1: Cho tam giác ABC, điểm D thuộc cạnh BC. Vẽ DE // AC; DF // AB (E nằm trên AB; F nằm trên AC). Gọi O là trụng điểm của EF. Tìm quỹ tích của O khi D di động trên cạnh BC.