Tìm số nguyên n sao cho : n3 + 2018n = 20202019 +4
NH
Những câu hỏi liên quan
tìm n thuộc tập hợp số nguyên sao cho \(n^3+2018n=2020^{2019_{ }^{ }}+4\)
Xem chi tiết
Ta có \(n^3+2018n=n\left(n-1\right)\left(n+1\right)+2019n⋮3\).
Lại có \(2020^{2019}+4\equiv1^{2019}+4\equiv2\left(mod3\right)\).
Từ đó suy ra không tồn tại n thoả mãn đề bài.
Đúng 2
Bình luận (0)
Tìm số nguyên n sao cho \(n^3+2018n=2020^{2019}+4\)
Ta có : \(n^3+2018n=n\left(n^2-1+2019\right)=\left(n-1\right)n\left(n+1\right)+2019n⋮3\forall n\inℤ\) (*)
Lại có : \(2020\equiv1\left(mod3\right)\)
\(\Rightarrow2020^{2019}\equiv1\left(mod3\right)\)
Và : \(4\equiv1\left(mod3\right)\)
Do đó : \(2020^{2019}+4\equiv2\left(mod3\right)\)
hay \(2020^{2019}+4⋮̸3\) . Điều này mâu thuẫn với (*)
Do đó, không tồn tại số nguyên n thỏa mãn đề.
Tìm số nguyên n sao cho n^3 + 2018n = 2020^2019 + 4
Mình đang cần gấp ai giải được thì giải chi tiết giúp mình nha
Tìm số tự nhiên n sao cho:
n^2 + 2018n + 2017 là số nguyên tố
Tìm số tự nhiên n sao cho:
S(n)=n^2 - 2018n +11
Nếu n= 0 thì không thỏa mản.
Nếu 1 ≤ n ≤2017 thì
S(n)=n^2 - 2018n +11 < n2 - 2018n +2017
Mà n2 - 2018n +2017 =(n-1)(n-2017)≤ 0 (loại)
Nếu n=2018 thì S(n) = 11,thỏa mãn.
Nếu n > 2018 thì
n-2018 ≥ 1 ⟹n2 - 2018n ≥ n
⟹ n2 - 2018n +11>n2 - 2018n
⟹S(n) > n (loại).Vậy n=2018
Đúng 0
Bình luận (0)
Tìm n ∈ N * sao cho : n3 – n2 + n – 1 là số nguyên tố
Ta có :
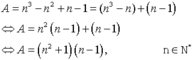
Nếu n = 1 suy ra A = 0
Nếu n = 2 suy ra A = 5 là số nguyên tố
Nếu n>2 thì A là tích của hai thừa số mà mỗi thừa số đều lớn hơn hai . Vậy A là hợp số
Vậy để A = n3 – n2 + n – 1 là số nguyên tố thì n = 2.
Đúng 0
Bình luận (0)
Tìm số nguyên n sao cho n^3-2018n-4=2020^2019
Tìm số tự nhiên n sao cho:
n^2 + 2018n + 2017 là hợp số
Tìm số nguyên n sao cho \(n^3+2018n=2020^{2019}+4\)


