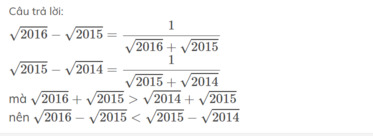so sanh\(\sqrt{24}\)+\(\sqrt{35}\)va 11
NL
Những câu hỏi liên quan
so sanh\(\sqrt{24+\sqrt{35}và11}\)
\(\sqrt{24+\sqrt{35}}< \sqrt{25+\sqrt{36}}=\sqrt{5+6}=\sqrt{11}< 11\)
Đúng 0
Bình luận (3)
So sanh:
a, \(\sqrt{\dfrac{35}{34}}\) va \(\sqrt{\dfrac{71}{70}}\)
b, \(4\sqrt{5}-3\sqrt{2}\) va 5
Khôi Bùi , DƯƠNG PHAN KHÁNH DƯƠNG, Mysterious Person, Phạm Hoàng Giang, Phùng Khánh Linh, Dũng Nguyễn, TRẦN MINH HOÀNG, JakiNatsumi, Hoàng Phong, ...
Đúng 0
Bình luận (0)
Giup minh voi !!! Khôi Bùi,DƯƠNG PHAN KHÁNH DƯƠNG, Phùng Khánh Linh, Nhã Doanh, hattori heiji, Phạm Hoàng Giang, Dũng Nguyễn, ...
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
\(\sqrt{24}+\sqrt{63}+3\)va 16 .so sanh
Ta có \(16=5+8+3=\sqrt{25}+\sqrt{64}+3.\)
do : \(25>24\Rightarrow\sqrt{25}>\sqrt{24}\); \(64>63\Rightarrow\sqrt{64}>\sqrt{63}\)
=> \(\sqrt{25}+\sqrt{64}+3>\sqrt{24}+\sqrt{63}+3\)
=> \(\sqrt{24}+\sqrt{63}+3< 16\)
Đúng 0
Bình luận (0)
ta có căn64>căn63 (1)
căn25>căn24 (2)
167>3 (3)
cộng vế theo vế (1);(2);(3)
=>căn64+căn25+167=16>căn24+căn63+3
Đúng 0
Bình luận (0)
1`)So Sanh
a)\(\sqrt{24}+\sqrt{45}\) va 12
b)\(\sqrt{37}-\sqrt{15}\)va 2
giup mk voi nhe
a,Ta có:
\(\left(\sqrt{24}+\sqrt{45}\right)^2=24+45=69\)
\(12^2=144\)
Do 69<144 nên ...
b,tương tự ý a
Đúng 0
Bình luận (0)
a ) Ta co \(\sqrt{24}+\sqrt{45}< \sqrt{25}+\sqrt{49}=5+7=12\)
vay \(\sqrt{24}+\sqrt{45}< 12\)
b)ta co \(\sqrt{37}-\sqrt{15}>\sqrt{4}-\sqrt{0}=2-0=2\)
vay \(\sqrt{37}-\sqrt{15}>2\)
Đúng 0
Bình luận (0)
So sanh:
a, \(2-2\sqrt{3}\) va \(4-\sqrt{15}\)
b, \(\sqrt{11}+2\) va \(3+\sqrt{3}\)
a) \(2-2\sqrt{3}\) và \(4-\sqrt{15}\)
Giả sử : \(2-2\sqrt{3}\ge4-\sqrt{15}\)
⇔ \(\sqrt{15}-2\sqrt{3}\ge2\)
⇔ \(\left(\sqrt{15}-2\sqrt{3}\right)^2\ge2^2\)
⇔ 15 - \(12\sqrt{5}+12\) ≥ 4
⇔ 27 -4 ≥ \(12\sqrt{5}\)
⇔ 23 ≥ \(12\sqrt{5}\)
⇔ \(23^2\) ≥ \(\left(12\sqrt{5}\right)^2\)
⇔ 529 ≥ 720 (sai)
Vậy 2 - \(2\sqrt{3}< 4-\sqrt{15}\)
b) \(\sqrt{11}+2\) và \(3+\sqrt{3}\)
Giả sử : \(\sqrt{11}+2\le3+\sqrt{3}\)
⇔ \(\sqrt{11}-\sqrt{3}\le1\)
⇔ \(\left(\sqrt{11}-\sqrt{3}\right)^2\le1\)
⇔ 14 - \(2\sqrt{33}\) ≤ 1
⇔ 13 ≤ \(2\sqrt{33}\)
⇔ \(13^2\le\left(2\sqrt{33}\right)^2\)
⇔ 169 ≤ 132 (sai)
Vậy \(\sqrt{11}+2\ge3+\sqrt{3}\)
Đúng 0
Bình luận (0)
Nguyễn Thanh Hằng, Dương Nguyễn, Ngô Thành Chung, Khôi Bùi , Trần Nguyễn Bảo Quyên, Tạ Thị Diễm Quỳnh, Nguyễn Quang Minh, Khánh Như Trương Ngọc, Nguyễn Quang Minh, Mysterious Person, Phùng Khánh Linh, JakiNatsumi, DƯƠNG PHAN KHÁNH DƯƠNG, Hoàng Phong, Ribi Nkok Ngok, ...
Đúng 0
Bình luận (0)
so sanh : A=\(\sqrt{11+\sqrt{96}}\) va B=\(\frac{2\sqrt{2}}{1+\sqrt{2}-\sqrt{3}}\)
\(A=\sqrt{11+\sqrt{96}}>B=\frac{2\sqrt{2}}{1+\sqrt{2}-\sqrt{3}}\)
Đúng 0
Bình luận (0)
Đã làm: https://olm.vn/hoi-dap/detail/223607632837.html
Đúng 0
Bình luận (0)
so sanh x va y biet
a) x=\(2\sqrt{7}\)va y=\(3\sqrt{3}\)
b) x=\(6\sqrt{2}\)va y=\(5\sqrt{3}\)
c) x=\(\sqrt{31}-\sqrt{33}\) va y=\(6-\sqrt{11}\)
So sanh : \(\sqrt{2016}-\sqrt{2015}va\sqrt{\sqrt{2015}-}\sqrt{2014}\)
so sanh ko dung may tinh
1 )\(\sqrt{3}\) +\(\sqrt{7}\) va 2+ \(\sqrt{6}\)
2) \(\sqrt{7}\) - \(\sqrt{5}\) va \(\sqrt{6}-2\)
3) \(\sqrt{11}-\sqrt{7}vs\sqrt{7}-\sqrt{3}\)
1: \(\left(\sqrt{3}+\sqrt{7}\right)^2=10+2\sqrt{21}\)
\(\left(2+\sqrt{6}\right)^2=10+4\sqrt{6}\)
mà 2 căn 21<4 căn 6
nên căn 3+căn 7<2+căn 6
2: \(\sqrt{7}-\sqrt{5}=\dfrac{2}{\sqrt{7}+\sqrt{5}}\)
\(\sqrt{6}-2=\dfrac{2}{\sqrt{6}+2}\)
mà \(\sqrt{7}+\sqrt{5}>\sqrt{6}+2\)
nên \(\sqrt{7}-\sqrt{5}< \sqrt{6}-2\)
3: \(\sqrt{11}-\sqrt{7}=\dfrac{4}{\sqrt{11}+\sqrt{7}}\)
\(\sqrt{7}-\sqrt{3}=\dfrac{4}{\sqrt{7}+\sqrt{3}}\)
mà căn 11>căn 3
nên \(\sqrt{11}-\sqrt{7}< \sqrt{7}-\sqrt{3}\)
Đúng 0
Bình luận (0)