Cho ΔABC có AB < BC < CA, thế thì:
A. Â> B̂
B. B̂< 60o
C. B̂= 60o
NM
Những câu hỏi liên quan
Cho tam giác ABC biết các cạnh a = 52,1cm, b = 85cm, c = 54cm. Tính các góc Â, B̂, Ĉ.
Cho tam giác ABC có Â = 120o, cạnh b = 8cm và c = 5cm. Tính cạnh a, các góc B̂, Ĉ của tam giác đó.
+ a2 = b2 + c2 - 2.bc.cosA = 82 + 52 – 2.5.8.cos120º = 129
⇒ a = √129 cm
Đúng 0
Bình luận (0)
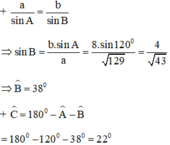
Bài 11. Cho tam giác ABC vuông tại A, có B̂ = 60o. Trên cạnh BC lấy điểm D sao cho BA=BD.
Tia phân giác của góc B cắt AC tại I.
a) Chứng minh: Tam giác BAD đều.
b) Chứng minh: Tam giác IBC cân.
c) Chứng minh: D là trung điểm của BC.
So sánh các cạnh của tam giác ABC, biết rằng: Â = 80º, B̂ = 45º
Theo định lý tổng ba góc trong tam giác ABC, ta có:
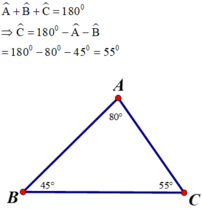
Cạnh đối diện góc B là AC
Cạnh đối diện góc C là AB
Cạnh đối diện góc A là BC
Trong một tam giác, cạnh đối diện với góc lớn hơn là cạnh lớn hơn.
Vì 450 < 550 < 800 hay B̂ < Ĉ < Â ⇒ AC < AB < BC.
Đúng 0
Bình luận (0)
Cho ΔABC có B̂ = Ĉ = 50 độ. Tia phân giác của  cắt BC tại D.
Chứng minh rằng: AD ⊥ BC
Xét ΔABC có góc B=góc C
nên ΔABC cân tại A
mà AD là đường phân giác
nên AD là đường cao
Đúng 0
Bình luận (0)
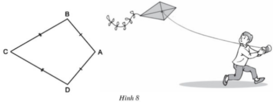
Ta gọi tứ giác ABCD trên hình 8 có AB = AD, CB = CD là hình "cái diều".
a) Chứng minh rằng AC là đường trung trực của BD.
b) Tính B̂,D̂ biết rằng  = 100º, Ĉ = 60º
a) Ta có:
AB = AD (gt) ⇒ A thuộc đường trung trực của BD
CB = CD (gt) ⇒ C thuộc đường trung trực của BD
Vậy AC là đường trung trực của BD
b) Xét ΔABC và ΔADC có:
AB = AD (gt)
BC = DC (gt)
AC cạnh chung
⇒ ΔABC = ΔADC (c.c.c)
Đúng 0
Bình luận (0)
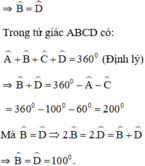
Bài 1: Giải ABC vuông tại A, biết:
a) AC = 100 cm và Ĉ = 300
b) AB = 50 cm và Ĉ = 450
c) B̂ = 350 và BC = 40 cm
d) AB = 70 cm và AC = 60 cm.
e) AB = 6 cm và B̂ = 600
f) AB = 5 cm và BC = 7 cm
b: \(\widehat{B}=45^0\)
AC=50cm
\(BC=50\sqrt{2}\left(cm\right)\)
Đúng 0
Bình luận (0)
Cho tứ giác ABCD có Â = B̂ = 90𝑜 , AB = BC = 1 2 AD, CE vuông góc AD tại E.
a) Chứng minh ABCD là hình thang vuông.
b) Chứng minh EC = EA = ED.
b) Tính các góc của hình thang.
b) Chứng minh AC vuông góc với CD.
c) Tính chu vi của hình thang nếu AB = 3 cm
hepl meeeeeeeeeeeeeee
a) Xét tứ giác ABCD có AD//BC(cùng vuông góc với BC)
nên ABCD là hình thang có hai đáy là AD và BC(Định nghĩa hình thang)
Hình thang ABCD(AD//BC) có \(\widehat{DAB}=\widehat{ABC}=90^0\)(gt)
nên ABCD là hình thang vuông(Dấu hiệu nhận biết hình thang vuông)
Đúng 0
Bình luận (0)
Cho tứ giác ABCD có B̂ = 1050 ; D̂ = 750 ; AB = BC = CD. Chứng minh rằng: a) AC là tia phân giác của của góc A b) ABCD là hình thang cân