thuyết minh 1 loài hoa
giúp mk vs mk đag gấp

giúp mk vs mk đag cần gấp
Giúp mk bài nầy vs mn ơi
Mk đag cần gấp
Giải giúp mk đề này vs ạ,mk đag cần gấp
Part 1
1 into
2 which
3 happily
4 aspect
5 if
6 compulsory
Part 2
1c 2f 3b 4g 5a 6e
Part 3
1 opened
2 to be finished
3 repairing
4 driving
5 harmful
6 modernize
7 environmentalists
8 effectively
Part 4
1 disappointing -> disappointed
2 come -> came
Part 5
1 succeed although he tried
2 my father could speak
3 seen such an interesting
4 being made to protect
Part 6
1 forest
2 climate
3 in
4 fortunatelt
Part 7
1T 2F 3F 4F
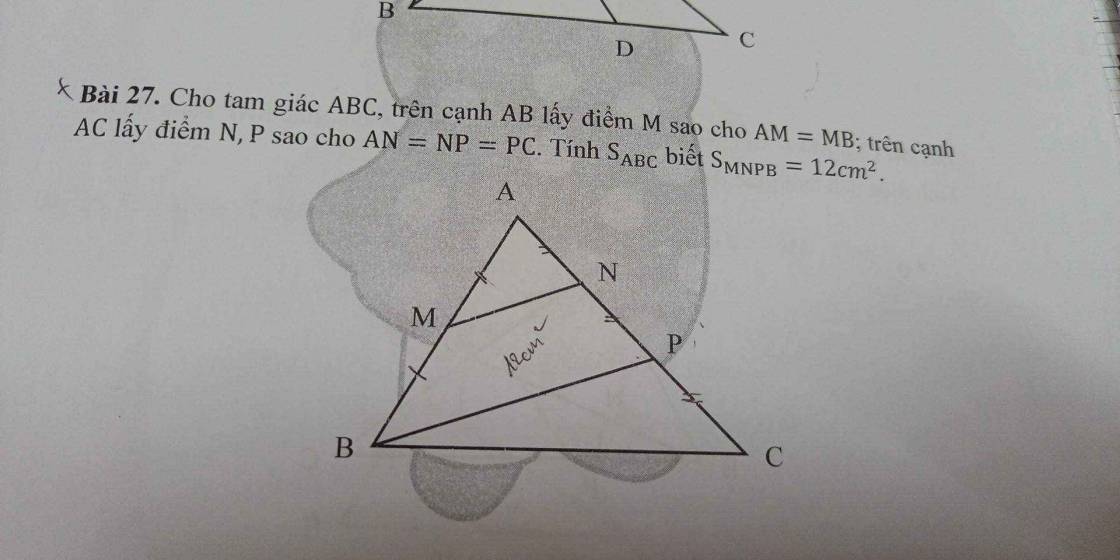 giúp mk vs ạ
giúp mk vs ạ
mk đag cần gấp lắm.cám ơn mng
Giúp mk vs Đag gấp
Dài qa nên jup 10 câu thoi nha =))
higher => highest
gives => gave
pleasing => pleased
lacing => to lace
quite so => bỏ quite
to turn on => turning on
would rather live on => would rather to live on
open for => open to
in => from
were => was
Mk đag cần gấp ạ. Mn giúp mk vs. Cảm ơn ạ
a) Ta có: \(P=\dfrac{a\sqrt{a}-1}{a-\sqrt{a}}-\dfrac{a\sqrt{a}+1}{a+\sqrt{a}}+\left(\sqrt{a}-\dfrac{1}{\sqrt{a}}\right)\left(\dfrac{3\sqrt{a}}{\sqrt{a}-1}-\dfrac{\sqrt{a}+2}{\sqrt{a}+1}\right)\)
\(=\dfrac{\left(\sqrt{a}-1\right)\left(a+\sqrt{a}+1\right)}{\sqrt{a}\left(\sqrt{a}-1\right)}-\dfrac{\left(\sqrt{a}+1\right)\left(a-\sqrt{a}+1\right)}{\sqrt{a}\left(\sqrt{a}+1\right)}+\dfrac{a-1}{\sqrt{a}}\cdot\dfrac{3\sqrt{a}\left(\sqrt{a}+1\right)-\left(\sqrt{a}+2\right)\left(\sqrt{a}-1\right)}{\left(\sqrt{a}-1\right)\left(\sqrt{a}+1\right)}\)
\(=\dfrac{a+\sqrt{a}+1-a+\sqrt{a}-1}{\sqrt{a}}+\dfrac{3a+3\sqrt{a}-\left(a-\sqrt{a}+2\sqrt{a}-2\right)}{\sqrt{a}}\)
\(=2+\dfrac{3a+3\sqrt{a}-a+\sqrt{a}-2\sqrt{a}+2}{\sqrt{a}}\)
\(=\dfrac{2\sqrt{a}+2a+2\sqrt{a}+2}{\sqrt{a}}\)
\(=\dfrac{2\left(a+2\sqrt{a}+1\right)}{\sqrt{a}}\)
\(=\dfrac{2\left(\sqrt{a}+1\right)^2}{\sqrt{a}}\)
b) Ta có: \(P-6=\dfrac{2\left(\sqrt{a}+1\right)^2-6\sqrt{a}}{\sqrt{a}}\)
\(=\dfrac{2a+4\sqrt{a}+2-6\sqrt{a}}{\sqrt{a}}\)
\(=\dfrac{2\left(a-\sqrt{a}+1\right)}{\sqrt{a}}>0\forall a\) thỏa mãn ĐKXĐ
hay P>6
Ai giúp mk vs ạ ❤️ mk đag cần rất gấp ạ d
d
Đặt \(log_2x=t\Rightarrow t\ge4\)
Phương trình trở thành: \(\sqrt{t^2-2t-3}=m\left(t-3\right)\)
\(\Leftrightarrow\sqrt{\left(t+1\right)\left(t-3\right)}=m\left(t-3\right)\)
\(\Leftrightarrow\sqrt{t+1}=m\sqrt{t-3}\)
\(\Leftrightarrow m=\sqrt{\dfrac{t+1}{t-3}}\)
Hàm \(f\left(t\right)=\sqrt{\dfrac{t+1}{t-3}}\) nghịch biến khi \(t\ge4\)
\(\lim\limits_{t\rightarrow+\infty}\sqrt{\dfrac{t+1}{t-3}}=1\) ; \(f\left(4\right)=\sqrt{5}\)
\(\Rightarrow1< f\left(t\right)\le\sqrt{5}\Rightarrow1< m\le\sqrt{5}\)
Đáp án D
Giúp mk bài nầy vs mn ơi mk đag cần gấp ạ
Giúp vs mk đag gấp lắm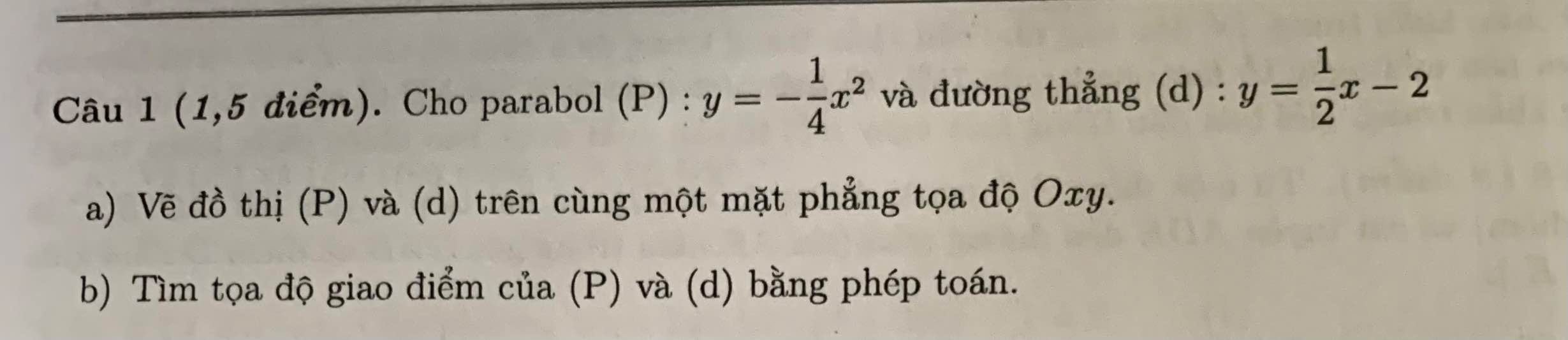
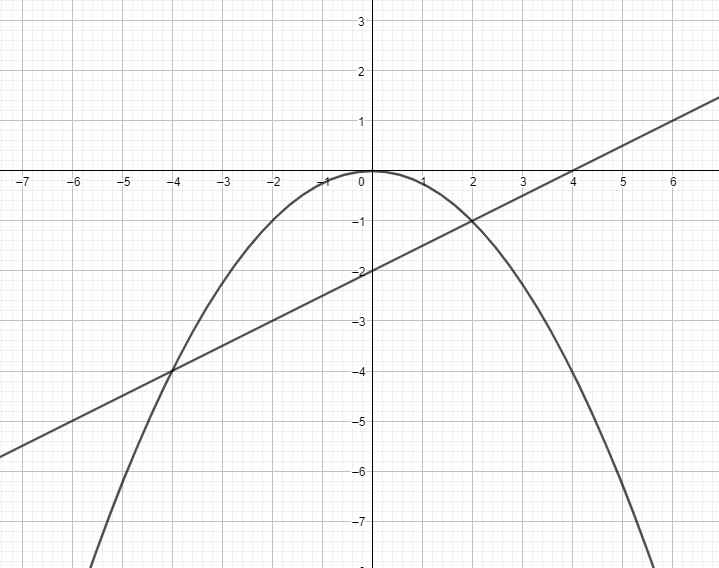
b.
Phương trình hoành độ giao điểm (P) và (d):
\(-\dfrac{1}{4}x^2=\dfrac{1}{2}x-2\Leftrightarrow x^2+2x-8=0\)
\(\Leftrightarrow\left(x-2\right)\left(x+4\right)=0\)
\(\Rightarrow\left[{}\begin{matrix}x=2\Rightarrow1=-1\\x=-4\Rightarrow y=-4\end{matrix}\right.\)
Vậy (P) và (d) cắt nhau tại 2 điểm có tọa độ là (2;-1) là (-4;-4)