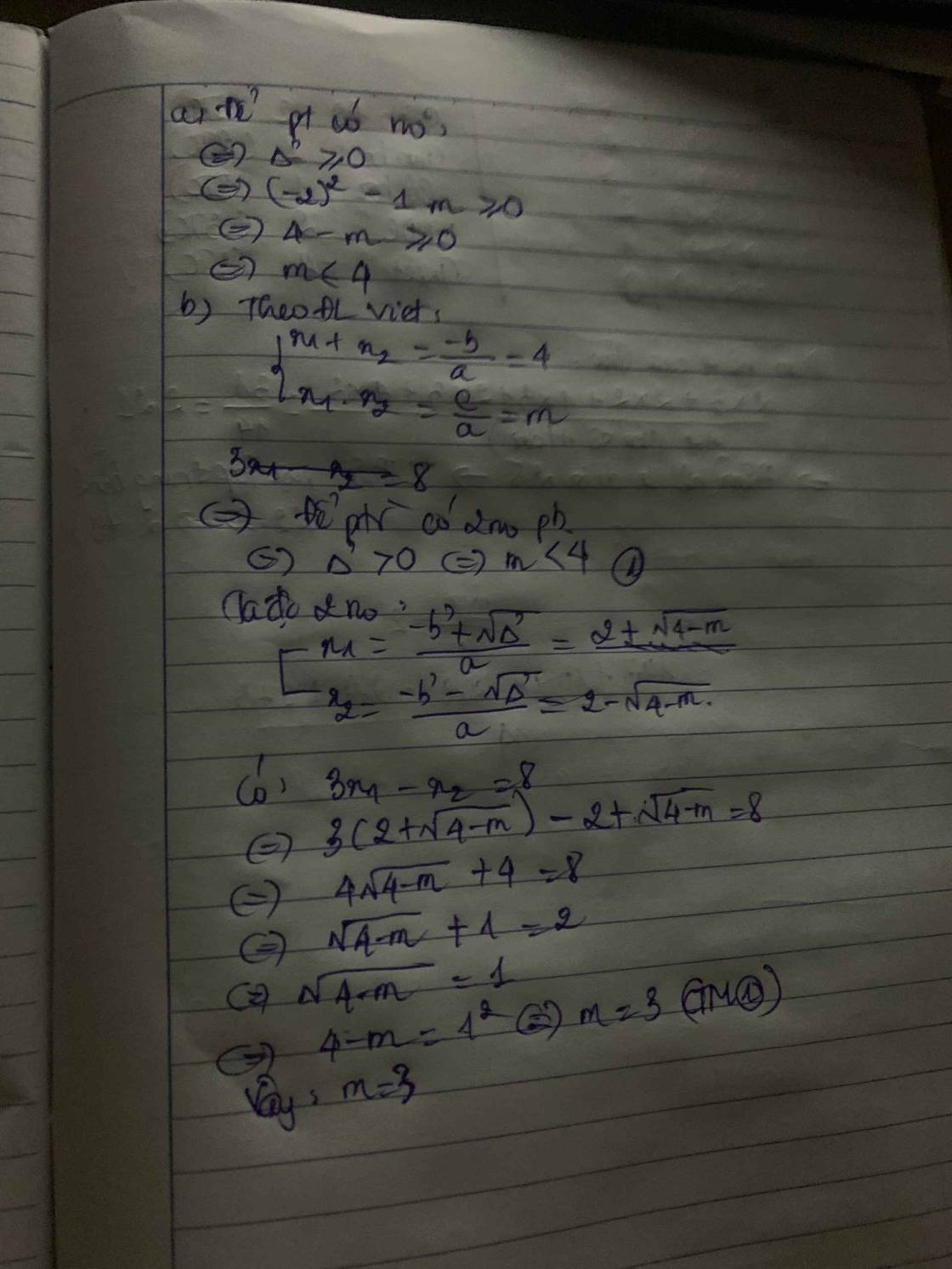Tìm m để pt sau có nghiệm \(x^4-4x^2+4mx-m^2=0\)
H24
Những câu hỏi liên quan
Tìm m nguyên để pt sau có ít nhất 1 nghiệm nguyên
\(4x^2+4mx+2m^2-5m+6=0\)
Tìm m để các phương trình sau (dùng công thức nghiệm thu gọn)
a.\(x^2+2\left(m-2\right)x+m^2-3=0\) có nghiệm
b.\(\left(2m-1\right)x-4mx+2m+3=0\) có nghiệm kép
c.\(4x^2-2\left(2m-1\right)x+m^2=0\) vô nghiệm
a: \(\Leftrightarrow\left(2m-4\right)^2-4\left(m^2-3\right)>=0\)
\(\Leftrightarrow4m^2-16m+16-4m^2+12>=0\)
=>-16m>=-28
hay m<=7/4
b: \(\Leftrightarrow16m^2-4\left(2m-1\right)\left(2m+3\right)=0\)
\(\Leftrightarrow16m^2-4\left(4m^2+4m-3\right)=0\)
=>4m-3=0
hay m=3/4
c: \(\Leftrightarrow\left(4m-2\right)^2-4\cdot4\cdot m^2< 0\)
=>-16m+4<0
hay m>1/4
Đúng 0
Bình luận (0)
Cho P=x2+4mx+m2=0 . Tìm m để pt có 2 nghiệm pb
1, x2+mx+40 tìm m để pt có 2 nghiệm tm frac{1}{x^4_1}+frac{1}{x^4_2}frac{257}{256}
2, 8x2 -8x+m2+10 tìm m để t có 2 nghiệm pb tm (4x1+5)(4x2+5)+190
3, x2 -6x +m -30 tìm m để pt có 2 nghiệm pb tm (x1-1)(x22-5x2+m-4)2
4, 2x2 -4mx +2m2-10 tìm m để pt có 2 nghiệm tm 2x12+4mx2+2m2-1ge0
5, x2 -2(m-1)x+m20 tìm m để pt có 2 nghiệm tm (x1-x2)2 +6mx1-2x2
Đọc tiếp
1, x2+mx+4=0 tìm m để pt có 2 nghiệm tm \(\frac{1}{x^4_1}+\frac{1}{x^4_2}=\frac{257}{256}\)
2, 8x2 -8x+m2+1=0 tìm m để t có 2 nghiệm pb tm (4x1+5)(4x2+5)+19=0
3, x2 -6x +m -3=0 tìm m để pt có 2 nghiệm pb tm (x1-1)(x22-5x2+m-4)=2
4, 2x2 -4mx +2m2-1=0 tìm m để pt có 2 nghiệm tm 2x12+4mx2+2m2-1\(\ge\)0
5, x2 -2(m-1)x+m2=0 tìm m để pt có 2 nghiệm tm (x1-x2)2 +6m=x1-2x2
Các bài này đều có phương pháp làm giống nhau
Bài 1:
Để pt có 2 nghiệm $x_1,x_2$ thì $\Delta=m^2-16\geq 0$
$\Leftrightarrow m\geq 4$ hoặc $m\leq -4(*)$
Áp dụng định lý Vi-et ta có: \(\left\{\begin{matrix} x_1+x_2=-m\\ x_1x_2=4\end{matrix}\right.\)
Khi đó:
\(\frac{1}{x_1^4}+\frac{1}{x_2^4}=\left(\frac{1}{x_1^2}+\frac{1}{x_2^2}\right)^2-\frac{2}{(x_1x_2)^2}=\frac{(x_1^2+x_2^2)^2}{(x_1x_2)^4}-\frac{2}{(x_1x_2)^2}\)
\(=\frac{[(x_1+x_2)^2-2x_1x_2]^2}{(x_1x_2)^4}-\frac{2}{(x_1x_2)^2}=\frac{(m^2-8)^2}{256}-\frac{2}{16}=\frac{257}{256}\)
\(\Leftrightarrow (m^2-8)^2-32=257\)
\(\Leftrightarrow (m^2-8)^2=289\Rightarrow m^2-8=\pm 17\)
\(\Rightarrow m^2=25\Rightarrow m=\pm 5\) (đều thỏa mãn $(*))$
Vậy $m=\pm 5$
Đúng 0
Bình luận (0)
Bài 3:
Để pt có 2 nghiệm phân biệt $x_1,x_2$ thì:
$\Delta'=9-(m-3)>0\Leftrightarrow m< 12$
Áp dụng định lý Vi-et: \(\left\{\begin{matrix} x_1+x_2=6\\ x_1x_2=m-3\end{matrix}\right.\)
Khi đó:
$(x_1-1)(x_2^2-5x_2+m-4)=2$
$\Leftrightarrow (x_1-1)(x_2^2-6x_2+m-3+x_2-1)=2$
$\Leftrightarrow (x_1-1)(x_2-1)=2$ (nhớ rằng $x_2^2-6x_2+m-3=0$ do $x_2$ là nghiệm của pt $x^2-6x+m-3=0$)
$\Leftrightarrow x_1x_2-(x_1+x_2)+1=2$
$\Leftrightarrow m-3-6+1=2$
$\Leftrightarrow m=10$ (thỏa mãn)
Vậy $m=10$
Đúng 0
Bình luận (0)
Bài 2:
Để pt có 2 nghiệm phân biệt thì:
$\Delta'=16-8(m^2+1)>0$
$\Leftrightarrow 2-(m^2+1)>0\Leftrightarrow m^2-1< 0$
$\Leftrightarrow -1< m< 1$
Áp dụng định lý Viet: \(\left\{\begin{matrix} x_1+x_2=1\\ x_1x_2=\frac{m^2+1}{8}\end{matrix}\right.\)
Khi đó:
$(4x_1+5)(4x_2+5)+19=0$
\(\Leftrightarrow 16x_1x_2+20(x_1+x_2)+44=0\)
\(\Leftrightarrow 2(m^2+1)+20+44=0\Leftrightarrow m^2=-33< 0\) (vô lý)
Vậy không tồn tại $m$ thỏa mãn ycđb
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
cho pt x2 - 4mx + 4m2 - m +2 =0
tìm m để pt có hai nghiệm phân biệt x1, x2 thỏa mãn |x1-x2| = 2
Δ=(-4m)^2-4(4m^2-m+2)
=16m^2-16m^2+4m-8=4m-8
Để phương trình có hai nghiệm phân biệt thì 4m-8>0
=>m>2
|x1-x2|=2
=>\(\sqrt{\left(x_1-x_2\right)^2}=2\)
=>\(\sqrt{\left(x_1+x_2\right)^2-4x_1x_2}=2\)
=>\(\sqrt{\left(4m\right)^2-4\left(4m^2-m+2\right)}=2\)
=>\(\sqrt{16m^2-16m^2+4m-8}=2\)
=>\(\sqrt{4m-8}=2\)
=>4m-8=4
=>4m=12
=>m=3(nhận)
Đúng 1
Bình luận (0)
tìm m để phương trình (m2-1)x+2=m-1 nhận x-2 là nghiệm
Tìm m để pt 3x2+4mx=8 có nghiệm x=-1
Tìm m để pt (2m+3)x-5-(m+2)-x có nghiệm là x=3
Gig gấp vs các bạn !!!
Kiểm tra giúp mình yêu cầu thứ nhất nhé!
Có thể bạn tìm:
"Đề: Tìm m để phương trình (m2-1)x+2=m-1 nhận x=2 là nghiệm.
Giải: Thế x=2 vào phương trình đã cho, ta suy ra (m2-1).2+2=m-1 (vô nghiệm).
Không có giá trị nào của m để phương trình đã cho nhận x=2 là nghiệm. -Hết-".
Thế x=-1 vào phương trình đã cho, ta suy ra 3.(-1)2+4m.(-1)=8 \(\Rightarrow\) m=-5/4.
Bạn xem giúp mình yêu cầu cuối cùng nha!
Có thể bạn tìm:
"Đề: Tìm m để phương trình (2m+3)x-5=(m+2)-x có nghiệm là x=3.
Giải: Thế x=3 vào phương trình đã cho, ta suy ra (2m+3).3-5=(m+2)-3 \(\Rightarrow\) m=-1. -Hết-".
Đúng 0
Bình luận (0)
Cho pt : \((x)^{2} -4mx + 4m -1=0 \) ( m là tham số )
Tìm m để pt có 2 nghiệm x1,x2 sao cho:
\((x_{1}^{2} -4mx_{2} +3)(x_{2}^{2}-4mx_{2}-2) =24\)
giúp mình pls :<
Cho pt x^2-4x+m=0 a)tìm m để pt có nghiệm b)tìm m để pt có nghiệm thỏa 3x1-x2=8
Cho pt: 4x^2-4mx-10 (m là tham số)a. C/M pt luôn có 2 nghiệm phân biệt x_1,x_2b. Tìm m để x_1left(4x_1+x_2right)-x_2left(4x_2-x_1right)32x_1^3x_2^3làm câu (b) được rồi ámà mình biến đổi tới khúc này: 4mleft(x_1-x_2right)0 (Yên tâm đúng ạ) left[{}begin{matrix}m0x_1-x_20end{matrix}right. left[{}begin{matrix}m0x_1x_2end{matrix}right. (Tới khúc này thì chia trhop gì đó nhưng em không biết làm ai cứu em với ạ:(
Đọc tiếp
Cho pt: \(4x^2-4mx-1=0\) (m là tham số)
a. C/M pt luôn có 2 nghiệm phân biệt \(x_1,x_2\)
b. Tìm m để \(x_1\left(4x_1+x_2\right)-x_2\left(4x_2-x_1\right)=32x_1^3x_2^3\)
làm câu (b) được rồi á
mà mình biến đổi tới khúc này:
\(4m\left(x_1-x_2\right)=0\) (Yên tâm đúng ạ)
=> \(\left[{}\begin{matrix}m=0\\x_1-x_2=0\end{matrix}\right.\) => \(\left[{}\begin{matrix}m=0\\x_1=x_2\end{matrix}\right.\) (Tới khúc này thì chia trhop gì đó nhưng em không biết làm ai cứu em với ạ:"(
\(m=0\) là okee rồi nè
còn \(x_1=x_2\) thì như sau :
\(\Leftrightarrow x_1-x_2=0\)
\(\Leftrightarrow\left(x_1-x_2\right)^2=0^2\)
\(\Leftrightarrow\left(x_1+x_2\right)^2-4x_1x_2=0\)
Tới đây rồi áp dụng cái Vi-ét vào là được m còn lại nhe.
Đúng 1
Bình luận (1)