Tìm m để phương trình
x2 -(m+1) x -m+1 =0 có 2 nghiệm dương phân biệt
cho phương trình x2-2(m+1)x+4m2-2m-2=0 ,m là tham số. Tìm m để phương trình
a. có 2 nghiệm phân biệt
b. có 2 nghiệm phân biệt dương
a, Phương trình có hai nghiệm phân biệt khi \(\Delta'=\left(m+1\right)^2-\left(4m^2-2m-2\right)=-3m^2+4m+3>0\)
\(\Leftrightarrow\dfrac{2-\sqrt{13}}{3}< m< \dfrac{2+\sqrt{13}}{3}\)
b, Yêu cầu bài toán thỏa mãn khi:
\(\left\{{}\begin{matrix}\Delta'>0\\2\left(m+1\right)>0\\4m^2-2m-2>0\end{matrix}\right.\)
\(\Leftrightarrow...\)
1:cho phương trình : x2 -2mx+m2-m-3=0
a, tìm m để phương trình có 2 nghiệm trái dấu
b, tìm m để phương trình có 2 nghiệm phân biệt dương
câu 2: cho pt: x2+(2m-1)x-m=0
a, chứng tỏ rằng pt luôn có 2 nghiệm với mọi m
b, Tìm m để pt có 2 nghiệm x1,x2 TM x1-x2=1
1.Ta có \(\Delta=4m^2-4\left(m^2-m-3\right)=4m+12\)
Để phương trình có 2 nghiệm phân biệt \(\Rightarrow\Delta>0\Rightarrow4m+12>0\Rightarrow m>-3\)
Theo hệ thức Viet ta có \(\hept{\begin{cases}x_1+x_2=2m\\x_1.x_2=m^2-m-3\end{cases}}\)
a. Phương trình có 2 nghiệm trái dấu \(\Rightarrow x_1.x_2< 0\Rightarrow m^2-m-3< 0\Rightarrow\frac{1-\sqrt{13}}{2}< m< \frac{1+\sqrt{13}}{2}\)
Vậy \(\frac{1-\sqrt{13}}{2}< m< \frac{1+\sqrt{13}}{2}\)
b. Phương trình có 2 nghiệm phân biệt dương \(\Leftrightarrow\hept{\begin{cases}x_1+x_2=2m>0\\x_1.x_2=m^2-m-3>0\end{cases}\Leftrightarrow\hept{\begin{cases}m>0\\m< \frac{1-\sqrt{13}}{2}\end{cases}\left(l\right);\hept{\begin{cases}m>0\\m>\frac{1+\sqrt{13}}{2}\end{cases}\Leftrightarrow m>\frac{1+\sqrt{13}}{2}}}}\)
Vậy \(m>\frac{1+\sqrt{13}}{2}\)
2. a.Ta có \(\Delta=\left(2m-1\right)^2+4m=4m^2-4m+1+4m=4m^2+1\)
Ta thấy \(\Delta=4m^2+1>0\forall m\)
Vậy phương trình luôn có 2 nghiejm phân biệt với mọi m
b. Theo hệ thức Viet ta có \(\hept{\begin{cases}x_1+x_2=1-2m\\x_1.x_2=-m\end{cases}}\)
Để \(x_1-x_2=1\Leftrightarrow\left(x_1-x_2\right)^2=1\Leftrightarrow\left(x_1+x2\right)^2-4x_1x_2=1\)
\(\Leftrightarrow\left(1-2m\right)^2-4.\left(-m\right)=1\Leftrightarrow4m^2-4m+1+4m=1\)
\(\Leftrightarrow m^2=0\Leftrightarrow m=0\)
Vậy \(m=0\)thoă mãn yêu cầu bài toán
1. Tìm tham số thực m để phương trình x2 1 - 4x + m - 4 = 0 có hai nghiệm phân biệt dương lớn hơn 1.
2. Tìm tham số thực m để phương trình x2 - 4x + m - 4 = 0 có hai nghiệm phân biệt dương bé hơn 4.
Cho phương trình x 2 + (2m – 1)x + m 2 – 2m + 2 = 0. Tìm m để phương trình có hai nghiệm phân biệt cùng dương
A. 1 2 < m < 7 4
B. m > 1 2
C. Cả A và B đúng
D. Không có giá trị nào của m
Phương trình x 2 + (2m – 1)x + m 2 – 2m + 2 = 0
(a = 1; b = 2m – 1; c = m 2 – 2m + 2)
Ta có ∆ = ( 2 m – 1 ) 2 – 4 . ( m 2 – 2 m + 2 ) = 4 m – 7
Gọi x 1 ; x 2 là hai nghiệm của phương trình, theo hệ thức Vi-ét ta có
Vì a = 1 ≠ 0 nên phương trình có hai nghiệm âm phân biệt ⇔ Δ > 0 P > 0 S > 0
⇔ 4 m − 7 > 0 1 − 2 m > 0 m 2 − 2 m + 2 > 0 ⇔ m > 7 4 m < 1 2 m − 1 2 + 1 > 0 ( l u o n d u n g ) ⇔ m > 7 4 m < 1 2 ( v o l y )
Vậy không có giá trị nào của m thỏa mãn đề bài
Đáp án: D
Bài 1 cho pt x^2-2(m+1)x+4m+m^2=0 .Tìm m để phương trình có 2 nghiệm phân biệt x1,x2 sao cho biểu thức A =|x1-x2| đạt giá trị nhỏ nhất
bài 2 cho pt x^2+mx+2m-4=0.Tìm m để phương trình có 2 nghiệm phân biệt x1,x2 thỏa mãn |x1|+|x2|=3
bài 3 cho pt x^2-3x-m^2+1=0.tìm m để phương trình có 2 nghiệm phân biệt x1,x2 thỏa mãn |x1|+2|x2|=3
2. Tìm giá trị của m để phương trình sau có 2 nghiệm cùng dấu. Khi đó 2 nghiệm mang dấu gì ? a) x - 2mx + 5m - 4= 0 (1) b) ma + mr +3 0 (2) 3. Cho phương trình: (m + 1)x2 + 2(m + 4)x + m+1 = 0 Tìm m để phương trình có: a) Một nghiệm b) Hai nghiệm phân biệt cùng dấu c) Hai nghiệm âm phân biệt 4. Cho phương trình (m - 4)x2 – 2(m- 2)x + m-1 = 0 Tìm m để phương trình a) Có hai nghiệm trái dấu và nghiệm âm có GTTÐ lớn hơn b) Có 2 nghiệm trái dấu và bằng nhau về GTTÐ c) Có 2 nghiệm trái dấu d) Có nghiệm kép dương. e) Có một nghiệm bằng 0 và một nghiệm dương.
Tìm m để phương trình (m-1) x 2 - 2mx + 3m - 2 = 0 có hai nghiệm dương phân biệt?
A. m < 0,1 < m < 2
B. 1 < m < 2
C. m > 2
D. m < 1/2
Đáp án: B
(m - 1) x 2 - 2mx + 3m - 2 = 0 (*)
Để phương trình (*) có hai nghiệm dương phân biệt thì:
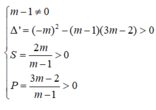
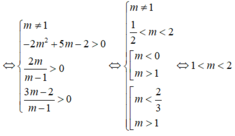
Tìm m để phương trình sau có hai nghiệm dương phân biệt
( m 2 + m + 1 ) x 2 + ( 2 m - 3 ) x + m - 5 = 0
Phương trình đã cho có hai nghiệm dương x 1 , x 2 phân biệt khi và chỉ khi
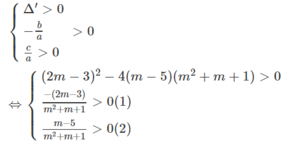
Vì m 2 + m + 1 > 0 nên bất phương trình (1) ⇔ m < 3/2 và bất phương trình (2) ⇔ m > 5
Do dó không có giá trị của m thỏa mãn yêu cầu bài toán
cho phương trình x^2-(m+2)x+m+8=0 , tìm m để phương trình có hai nghiệm phân biệt dương thỏa mãn x1^3-x2=0
cho phương trình x2 -(m+1)x +m+2=0
a) tìm m để phương trình vô nghiệm ? có nghiệm kép? có nghiệm? có 2 nghiệm phân biệt?
b) tìm m để phương trình có 2 nghiệm trái dấu
c) tìm m để phương trình có 2 nghiệm dương phân biệt
d) tìm m để phương trình có ít nhất một nghiệm dương