Cho tam giác ABC(AC>AB) đường phân giác AD.Trên cạnh AD lấy điểm E sao cho CDE=BAC.CMR DB=DE
TK
Những câu hỏi liên quan
cho tam giác nhọn ABC có AB<AC, đường cao AD.trên đoạn DC lấy điểm E sao cho DB=DE .chứng minh AD,EF,CK đồng quy 1 điểm
Cho tam giác ABC có AB > AC. Đg phân giác AD. Lấy E trên cạnh AC sao cho góc CDE = góc BAC
a)Tìm tam giác đòng dạng với tam giác ABC
b)Cm: DE = DB
a: Xét ΔCDE và ΔCAB có
\(\widehat{CDE}=\widehat{CAB}\)
\(\widehat{C}\) chung
Do đó: ΔCDE\(\sim\)ΔCAB
Câu b đề sai rồi bạn
Đúng 0
Bình luận (0)
Cho tam giác ABC(AB<AC),A=a,tia phân giác góc A cắt BC ở D,lấy điểm E thuộc cạnh AC sao cho CDE=a.CM DB=DE
Cho tam giác ABC với AC>AB, Đường p/g AD.Trên AC lấy E sao cho CDE=BAC
Cmr:BD=DE
cho tam giác ABC có AB<AC , đường phân giác AD . Trên cạnh AC lấy điểm E sao cho AE=AB . Gọi K là giao điểm của các đường thẳng AB và DE . Chứng minh
a)DB=DE
b)tam giác BDK và tam giác EDC
c)DC>DB
a) Xét tam giác ABD và tam giác AED có
AB=AE
BAD=DAE( vì AD là phân giác của BAC)
Cạnh AD chung
=> tam giác ABD= tam giác AED( c.g.c)
=>DB=DE
b) Có tam giác ABD= tam giác AED
=> ABD=AED
=>DBK=DEC( kề bù với 2 góc bằng nhau)
Xét tam giác BDK và tam giác EDC
BD=DE
BDK=EDC ( 2 góc đối đỉnh)
DBK=DEC
=> tam giác BDK= tam giác EDC ( g.c.g)
c) Tam giác BDK=tam giác EDC
=>DBK=DEC
Có DBK>C( DBK là góc ngoài tam giác ABC)
=>DEC>C
=>DC>DE
Mà DE=DE
=>DC>DB
Đúng 0
Bình luận (0)
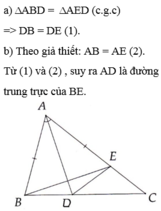
Cho tam giác ABC, đường phân giác AD. Trên tia AC lấy điểm E sao cho AE = AB. Chứng minh:
a) DB = DE;
b) AD là đường trung trực của BE.
Vẽ Cho tam giác ABC nhọn Ab < ac trên cạnh ac lấy E sao cho ae = ab tia phân giác góc bac cắt bc tại d gọi giao điểm ad va be là m
CM de = db
Xem chi tiết
Cho tam giác ABC (AB<AC), phân giác AD.Trên cạnh AC lấy điểm E sao cho AB=AE. Tia ED cắt tia AB tại K
1. Chứng minh BD=DE
2.Chứng minh: góc DKC = DCK
3. Chứng minh AD Vuông góc với KC
Cho tam giác ABC (AB<AC), vẽ tia phân giác AD của tam giác ABC. Trên cạnh AC lấy điểm E sao cho AE=AB.
a) Chứng minh tam giác ADB = tam giác ADE
b) Chứng minh AD là đường trung trực của BE
c) Gọi F là giao điểm của AB và DE. Chứng minh tam giác BFD=tam giác ECD
d) So sánh DB và DC