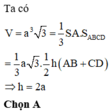Cho hình thang ABCD có 2 đáy là AB = 2a; CD = a. Hãy xác định vị trí điểm M trên đường thẳng CD sao cho Đường thẳng AM chia hình thang thành 2 phần có diện tích bằng nhau.
HT
Những câu hỏi liên quan
Cho hình chóp S.ACBD có đáy ABCD là hình thang đáy AB và CD với A B = 2 C D = 2 a , cạnh bên SA vuông góc với mặt phẳng đáy và S A = a 3 . Tính chiều cao h của hình thang ABCD biết khối chóp S.ABCD có thể tích bằng
A. h = 2a
B. h = 4a
C. h = 6a
D. h = a
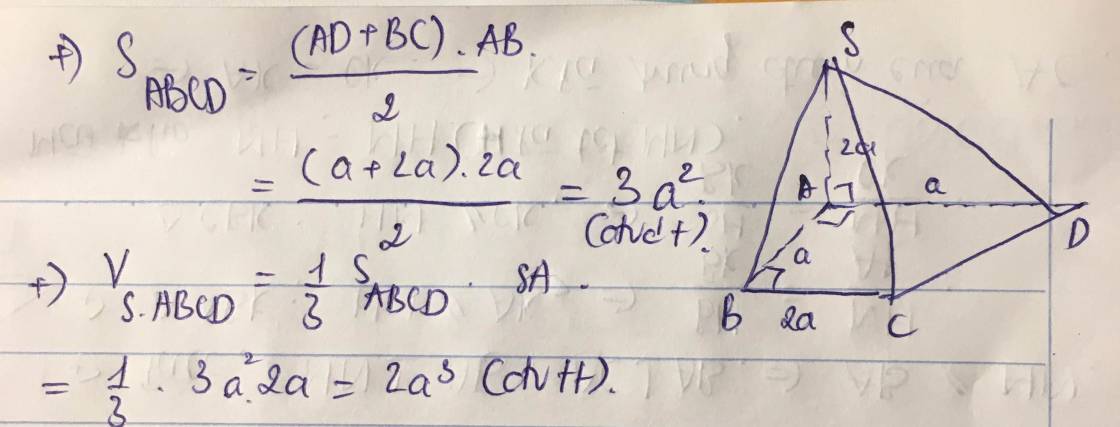
Tính VSABCD�Δ���� biết SA ⊥ đáy, ABCD là hình thang vuông có 2 đáy ADa, BC2a và ABa, SA2a
Đọc tiếp
Tính biết SA ⊥ đáy, ABCD là hình thang vuông có 2 đáy AD=a, BC=2a và AB=a, SA=2a
\(V=\dfrac{1}{3}SA.S_{ABCD}=\dfrac{1}{3}SA.\dfrac{1}{2}\left(AD+BC\right).AB=a^3\)
Đúng 0
Bình luận (0)
Tính thể tích S.ABCD biết SA ⊥ đáy, ABCD là hình thang vuông có 2 đáy AD=a, BC=2a và AB=a, SA=2a
Cho hình chóp S.ABCD có đáy ABCD là hình thang cân với AD 2a, AB BC a, SA
⊥
(ABCD), SA a
2
. Tính thể tích V của hình chóp S.ABD. A. V
a
3
2
3
B. V
a
3
3
6
C. V
a...
Đọc tiếp
Cho hình chóp S.ABCD có đáy ABCD là hình thang cân với AD = 2a, AB = BC = a, SA ⊥ (ABCD), SA = a 2 . Tính thể tích V của hình chóp S.ABD.
A. V = a 3 2 3
B. V = a 3 3 6
C. V = a 3 3
D. V = a 3 6
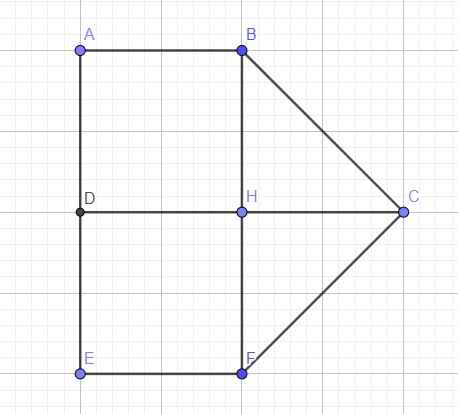
cho hình thang vuông ABCD có AD=a là đường cao, đáy nhỏ AB=a, đáy lớn CD=2a. Thể tích của khối tròn xoay khi hình thang quay quanh CD là
Khi quay quanh CD sẽ tạo ra hình khối gồm 2 khối:
- Khối trụ chiều cao \(AB=a\) bán kính đáy \(r=AD=a\Rightarrow V_1=\pi.AB^2.AD^2=\pi a^3\)
- Khối nón chiều cao \(CH=\dfrac{1}{2}CD=a\) bán kính đáy \(BH=AD=a\Rightarrow V_2=\dfrac{1}{3}\pi.a^2.a=\dfrac{\pi a^3}{3}\)
\(\Rightarrow V=V_1+V_2=\pi a^3+\dfrac{\pi a^3}{3}=\dfrac{4\pi a^3}{3}\)
Đúng 0
Bình luận (0)
Cho hình chóp S.ABCD có đáy ABCD là hình thang cân, SA 2a và SA vuông góc với mặt đáy (ABCD). Biết AD 2a, AB BC CD a. Diện tích S của mặt cầu ngoại tiếp hình chóp S.ABCD bằng bao nhiêu?
Đọc tiếp
Cho hình chóp S.ABCD có đáy ABCD là hình thang cân, SA = 2a và SA vuông góc với mặt đáy (ABCD). Biết AD = 2a, AB = BC = CD = a. Diện tích S của mặt cầu ngoại tiếp hình chóp S.ABCD bằng bao nhiêu?
![]()
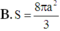
![]()
![]()
Đáp án A

ABCD là hình thanh cân có AB = BC = CD = a; AD = 2a nên M là tâm của đáy ABCD.
SA = AD = 2a; SA ⊥ (ABCD) => tam giác SAD vuông cân tại A nên tâm mặt cầu ngoại tiếp hình chóp S.ABCD là trung điểm N của SD
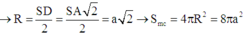
Đúng 0
Bình luận (0)
Cho hình chóp SABCD có đáy là hình thang cân, AD là đáy lớn, SB=a căn 2, AD=2a, AB=BC=CD=a, hình chiếu của S -> (ABCD) là trung điểm AB. Khoảng cách từ SB ->AD
Cho hình chóp SABCD có SA vuông góc với (ABCD), SA=a\(\sqrt{2}\), đáy abcd là hình thang vuông tại A và D với AB=2a, AD=DC=a. Tính góc giữa (SBC) và (ABCD)
Cho hình thang ABCD có 2 đáy là AB = 2a; CD = a. Hãy xác định vị trí điểm M trên đường thẳng CD sao cho Đường thẳng AM chia hình thang thành 2 phần có diện tích bằng nhau.