cho các số thực a,b,c thỏa mãn : a + b + c = 7 ; ab + bc + ca = 15 . Chứng minh rằng : a <= 11/3
VT
Những câu hỏi liên quan
cho các số thực a b c thỏa mãn a+b+c=0 và a^7 + b^7 + c^7 = 0 tính a^2023 + b^2023 + c^2023
cần gấp ạ -(
Ta có thể sử dụng công thức Newton về đa thức để giải bài toán này. Đặt đa thức $P(x) = (x-a)(x-b)(x-c) = x^3 - (a+b+c)x^2 + (ab+bc+ca)x - abc$.
Do $a+b+c=0$, nên $P(x) = x^3 - 3kx - abc$ với $k = \frac{ab+bc+ca}{a+b+c}$.
Ta có thể tính được $a^2+b^2+c^2 = -2(ab+bc+ca)$.
Đặt $S_n = a^n + b^n + c^n$. Ta có thể suy ra các công thức sau:
$S_1 = 0$
$S_2 = a^2 + b^2 + c^2 = -2(ab+bc+ca)$
$S_3 = 3abc$
$S_4 = (a^2+b^2+c^2)^2 - 2(a^2b^2+b^2c^2+c^2a^2) = 2(ab+bc+ca)^2 - 3abc(a+b+c)$
$S_5 = 5(ab+bc+ca)(a^2+b^2+c^2) - 5abc(a+b+c)$
$S_6 = (a^2+b^2+c^2)^3 - 3(a^2+b^2+c^2)(a^2b^2+b^2c^2+c^2a^2) + 2(a^2b^2c^2)$
$S_7 = 7(ab+bc+ca)(a^2+b^2+c^2)^2 - 14abc(a^2+b^2+c^2) + 7a^2b^2c^2$
Từ đó, ta có thể tính được $S_1, S_2, S_3, S_4, S_5, S_6$ dựa trên các giá trị đã biết.
Đặt $T_n = a^n+b^n+c^n - S_n$. Ta có thể suy ra các công thức sau:
$T_1 = 0$
$T_2 = 2S_2$
$T_3 = 3S_3$
$T_4 = 2S_2^2 - 4S_4$
$T_5 = 5S_2S_3 - 5S_5$
$T_6 = 2S_2S_4 + 3S_3^2 - 6S_6$
$T_7 = 7S_2S_5 - 14S_3S_4 + 7S_7$
Do $S_1=S_3=0$, nên $T_1=T_3=0$.
Từ $a+b+c=0$, ta có $a^2+b^2+c^2 = -2(ab+bc+ca)$. Do đó, $S_2 = 2(ab+bc+ca)$ và $S_4 = 2(ab+bc+ca)^2 - 3abc(a+b+c) = 2(ab+bc+ca)^2$.
Từ $a^7+b^7+c^7=0$, ta có $T_7 = 7S_2S_5 - 14S_3S_4 + 7S_7 = 7S_2S_5 - 14S_4S_3 + 7S_7 = 7S_7$.
Từ $T_7 = 7S_7$, ta có $S_7 = \frac{T_7}{7} = 0$.
Do đó, $T_6 = 2S_2S_4 + 3S_3^2 - 6S_6 = 2(2(ab+bc+ca))(2(ab+bc+ca)^2) + 3(abc)^2 - 6S_6 = 12(ab+bc+ca)^2 + 3(abc)^2 - 6S_6$.
Từ $T_6 = 12(ab+bc+ca)^2 + 3(abc)^2 - 6S_6$, ta có $S_6 = \frac{1}{6}(12(ab+bc+ca)^2 + 3(abc
Đúng 1
Bình luận (0)
Giải
Vì a + b + c = 0 nên a + b = -c
Ta có:
\(a^7+b^7=\left(a+b\right)\left(a^6-a^5b+a^4b^2-a^3b^3+a^2b^4-ab^5+b^6\right)\\ =-c\left(a^6-a^5b+a^4b^2-a^3b^3+a^2b^4-ab^5+b^6\right)\\ =c\left(-a^6+a^5b-a^4b^2+a^3b^3-a^2b^4+ab^5-b^6\right)\\ =c\left[-\left(a^6+6a^5b+15a^4b^2+20a^3b^3+15a^2b^4+6ab^5+b^6\right)+\left(7a^5b+14a^4b^2+21a^3b^3+14a^2b^4+7ab^5\right)\right]\\ =c\left[-\left(a+b\right)^6+7ab\left(a^4+2a^3b+3a^2b^2+2ab^3+b^4\right)\right]\\ =c\left\{-\left(a+b\right)^6+7ab\left[\left(a^2+b^2\right)^2+2ab\left(a^2+b^2\right)+3a^2b^2-2a^2b^2\right]\right\}\\ =c\left\{-\left(a+b\right)^6+7ab\left[\left(a^2+b^2\right)\left(a+b\right)^2+a^2b^2\right]\right\}\\ =c\left\{-c^6+7ab\left[\left(a^2+b^2\right)\left(a+b\right)^2+a^2b^2\right]\right\}\\ =-c^7+7abc\left[\left(a^2+b^2\right)\left(a+b\right)^2+a^2b^2\right]\\ \Rightarrow a^7+b^7+c^7=7abc\left[\left(a^2+b^2\right)\left(a+b\right)^2+a^2b^2\right]\Rightarrow7abc\left[\left(a^2+b^2\right)\left(a+b\right)^2+a^2b^2\right]=0\)TH1: \(\left(a^2+b^2\right)\left(a+b\right)^2+a^2b^2=0\)
Vì \(a^2,b^2,\left(a+b\right)^2,a^2b^2\ge0\) nên \(\left(a^2+b^2\right)\left(a+b\right)^2+a^2b^2\ge0\)
Dấu "=" xảy ra khi và chỉ khi a = b = 0
Mà a + b + c = 0 nên suy ra c = 0
Vậy \(a^{2023}+b^{2023}+c^{2023}=0\)
TH2: abc = 0
Vì abc = 0 nên sẽ có ít nhất một trong ba số a, b, c = 0
Vì a, b, c có vai trò như nhau nên không mất tính tổng quát, giả sử \(c=0\)
Mà a + b + c = 0 nên a + b =0 hay a = -b
\(\Rightarrow a^{2023}+b^{2023}+c^{2023}=0\)
Kết luận: \(a^{2023}+b^{2023}+c^{2023}=0\)
Đúng 0
Bình luận (0)
cho các số thực a b c thỏa mãn 1/a + 1/b +1/c = 1/a+b+c CMR 1/a^7+1/b^7+1/c^7=1/a^7+b^7+c^7
cho các số thực a,b,c khác 0 thỏa mãn 1/a+1/b+1/c=1/a+b+c chứng minh rằng 1/a^7 +1/b^7 + 1/c^7 = 1/a^7+b^7+c^7
Ta có \(\frac{1}{a}+\frac{1}{b}+\frac{1}{c}=\frac{1}{a+b+c}\)
<=> \(\frac{1}{a}+\frac{1}{b}=\frac{1}{a+b+c}-\frac{1}{c}\)
<=> \(\frac{a+b}{ab}=-\frac{a+b}{\left(a+b+c\right)c}\)
<=> \(\left(a+b\right)\left[\frac{1}{ab}+\frac{1}{\left(a+b+c\right).c}\right]=0\)
<=> \(\frac{\left(a+b\right)\left(b+c\right)\left(c+a\right)}{ab\left(a+b+c\right)c}=0\)
<=> (a + b)(b + c)(c + a) = 0
<=> a = -b hoặc b = -c hoặc c = -a
Với a = -b => \(\frac{1}{a^7}+\frac{1}{b^7}+\frac{1}{c^7}=\frac{1}{-b^7}+\frac{1}{b^7}+\frac{1}{c^7}=\frac{1}{c^7}\left(1\right)\)
\(\frac{1}{a^7+b^7+c^7}=\frac{1}{-b^7+b^7+c^7}=\frac{1}{c^7}\left(2\right)\)
Từ (1) và (2) => \(\frac{1}{a^7}+\frac{1}{b^7}+\frac{1}{c^7}=\frac{1}{a^7+b^7+c^7}\)
Tương tự với b =- c và c = -a ta cũng chứng minh được đẳng thức trên
=> ĐPCM
bài 1: tìm tất cả các cặp số thực (a,b) thỏa mãn: a2+b2+9=ab+3a+3b
bài 2: cho các số thực a,b,c thỏa mãn (a+b+c)2=3(ab+bc+ca). chứng minh a=b=c
Bài 2 :
\(\left(a+b+c\right)^2=3\left(ab+bc+ca\right)\)
<=> a^2 + b^2 + c^2 + 2ab + 2bc + 2ca = 3ab + 3bc + 3ca
<=> a^2 + b^2 + c^2 = ab + bc + ca
<=> 2a^2 + 2b^2 + 2c^2 = 2ab + 2bc + 2ca
<=> ( a - b )^2 + ( b - c )^2 + ( c - a )^2 = 0
<=> a = b = c
Đúng 3
Bình luận (0)
Bài 1 :
a^2 + b^2 + 9 = ab + 3a + 3b
<=> 2a^2 + 2b^2 + 18 = 2ab + 6a + 6b
<=> a^2 - 2ab + b^2 + a^2 - 6a + 9 + b^2 - 6a + 9 = 0
<=> ( a - b)^2 + ( a - 3)^2 + ( b - 3)^2 = 0
Dấu ''='' xảy ra khi a = b = 3
Đúng 1
Bình luận (0)
1.
\(\Leftrightarrow2a^2+2b^2+18=2ab+6a+6b\)
\(\Leftrightarrow\left(a^2-2ab+b^2\right)+\left(a^2-6a+9\right)+\left(b^2-6b+9\right)=0\)
\(\Leftrightarrow\left(a-b\right)^2+\left(a-3\right)^2+\left(b-3\right)^2=0\)
\(\Leftrightarrow\left\{{}\begin{matrix}a-b=0\\a-3=0\\b-3=0\end{matrix}\right.\) \(\Leftrightarrow a=b=3\)
2.
\(\left(a+b+c\right)^2=3\left(ab+bc+ca\right)\)
\(\Leftrightarrow a^2+b^2+c^2+2ab+2bc+2ca=3ab+3bc+3ca\)
\(\Leftrightarrow2a^2+2b^2+2c^2-2ab-2bc-2ca=0\)
\(\Leftrightarrow\left(a^2-2ab+b^2\right)+\left(b^2-2bc+c^2\right)+\left(c^2-2ca+a^2\right)=0\)
\(\Leftrightarrow\left(a-b\right)^2+\left(b-c\right)^2+\left(c-a\right)^2=0\)
\(\Leftrightarrow\left\{{}\begin{matrix}a-b=0\\b-c=0\\c-a=0\end{matrix}\right.\) \(\Leftrightarrow a=b=c\)
Đúng 1
Bình luận (0)
Xem thêm câu trả lời
1. Cho các số thực không âm a;b;c (không có hai số nào đồng thời bằng 0) thỏa mãn a+b+c leq 3Tìm giá trị nhỏ nhất: Adfrac{1}{a^2+b^2}+dfrac{1}{b^2+c^2}+dfrac{1}{c^2+a^2}2. Cho các số thực a;b;c in [0;1] thỏa mãn a+b+c2, tìm giá trị lớn nhất và nhỏ nhất của:Bdfrac{ab}{1+ab}+dfrac{bc}{1+bc}+dfrac{ca}{1+ca}Thank you all :)
Đọc tiếp
1. Cho các số thực không âm \(a;b;c\) (không có hai số nào đồng thời bằng 0) thỏa mãn \(a+b+c \leq 3\)
Tìm giá trị nhỏ nhất: \(A=\dfrac{1}{a^2+b^2}+\dfrac{1}{b^2+c^2}+\dfrac{1}{c^2+a^2}\)
2. Cho các số thực \(a;b;c \in [0;1]\) thỏa mãn \(a+b+c=2\), tìm giá trị lớn nhất và nhỏ nhất của:
\(B=\dfrac{ab}{1+ab}+\dfrac{bc}{1+bc}+\dfrac{ca}{1+ca}\)
Thank you all :)
1.
Ta sẽ chứng minh BĐT sau: \(\dfrac{1}{a^2+b^2}+\dfrac{1}{b^2+c^2}+\dfrac{1}{c^2+a^2}\ge\dfrac{10}{\left(a+b+c\right)^2}\)
Do vai trò a;b;c như nhau, ko mất tính tổng quát, giả sử \(c=min\left\{a;b;c\right\}\)
Đặt \(\left\{{}\begin{matrix}x=a+\dfrac{c}{2}\\y=b+\dfrac{c}{2}\end{matrix}\right.\) \(\Rightarrow x+y=a+b+c\)
Đồng thời \(b^2+c^2=\left(b+\dfrac{c}{2}\right)^2+\dfrac{c\left(3c-4b\right)}{4}\le\left(b+\dfrac{c}{2}\right)^2=y^2\)
Tương tự: \(a^2+c^2\le x^2\) ; \(a^2+b^2\le x^2+y^2\)
Do đó: \(A\ge\dfrac{1}{x^2}+\dfrac{1}{y^2}+\dfrac{1}{x^2+y^2}\)
Nên ta chỉ cần chứng minh: \(\dfrac{1}{x^2}+\dfrac{1}{y^2}+\dfrac{1}{x^2+y^2}\ge\dfrac{10}{\left(x+y\right)^2}\)
Mà \(\dfrac{1}{\left(x+y\right)^2}\le\dfrac{1}{4xy}\) nên ta chỉ cần chứng minh:
\(\dfrac{1}{x^2}+\dfrac{1}{y^2}+\dfrac{1}{x^2+y^2}\ge\dfrac{5}{2xy}\)
\(\Leftrightarrow\dfrac{1}{x^2}+\dfrac{1}{y^2}-\dfrac{2}{xy}+\dfrac{1}{x^2+y^2}-\dfrac{1}{2xy}\ge0\)
\(\Leftrightarrow\dfrac{\left(x-y\right)^2}{x^2y^2}-\dfrac{\left(x-y\right)^2}{2xy\left(x^2+y^2\right)}\ge0\)
\(\Leftrightarrow\dfrac{\left(x-y\right)^2\left(2x^2+2y^2-xy\right)}{2x^2y^2}\ge0\) (luôn đúng)
Vậy \(A\ge\dfrac{10}{\left(a+b+c\right)^2}\ge\dfrac{10}{3^2}=\dfrac{10}{9}\)
Dấu "=" xảy ra khi \(\left(a;b;c\right)=\left(\dfrac{3}{2};\dfrac{3}{2};0\right)\) và các hoán vị của chúng
Đúng 1
Bình luận (0)
2.
Ta có: \(B=\dfrac{ab+1-1}{1+ab}+\dfrac{bc+1-1}{1+bc}+\dfrac{ca+1-1}{1+ca}\)
\(B=3-\left(\dfrac{1}{1+ab}+\dfrac{1}{1+ca}+\dfrac{1}{1+ab}\right)\)
Đặt \(C=\dfrac{1}{1+ab}+\dfrac{1}{1+bc}+\dfrac{1}{1+ca}\)
Ta có: \(C\ge\dfrac{9}{3+ab+bc+ca}\ge\dfrac{9}{3+\dfrac{1}{3}\left(a+b+c\right)^2}=\dfrac{27}{13}\)
\(\Rightarrow B\le3-\dfrac{27}{13}=\dfrac{12}{13}\)
\(B_{max}=\dfrac{12}{13}\) khi \(a=b=c=\dfrac{2}{3}\)
Do \(a;b;c\in\left[0;1\right]\)
\(\Rightarrow\left(a-1\right)\left(b-1\right)\ge0\)\(\Leftrightarrow ab+1\ge a+b\)
\(\Leftrightarrow ab+c+1\ge a+b+c=2\)
\(\Rightarrow abc+ab+c+1\ge ab+c+1\ge2\)
\(\Rightarrow\left(c+1\right)\left(ab+1\right)\ge2\)
\(\Rightarrow\dfrac{1}{ab+1}\le\dfrac{c+1}{2}\)
Hoàn toàn tương tự, ta có:
\(\dfrac{1}{bc+1}\le\dfrac{a+1}{2}\) ; \(\dfrac{1}{ca+1}\le\dfrac{b+1}{2}\)
Cộng vế: \(C\le\dfrac{a+b+c+3}{2}=\dfrac{5}{2}\)
\(\Rightarrow B\ge3-\dfrac{5}{2}=\dfrac{1}{2}\)
\(B_{min}=\dfrac{1}{2}\) khi \(\left(a;b;c\right)=\left(0;1;1\right)\) và các hoán vị của chúng
Đúng 1
Bình luận (0)
Cho các số thực dương a, b, c thỏa mãn a + b + c = 3. Chứng minh rằng: \(\sqrt{2a^2+\dfrac{7}{b^2}}+\sqrt{2b^2+\dfrac{7}{c^2}}+\sqrt{2c^2+\dfrac{7}{a^2}}\ge9\)
TK: Cho các số thực dương a, b, c thỏa mãn a + b+ c = 3. Chứng minh rằng: \(\sqrt{2a^2+\frac{7}{b^2}}+\sqrt{2b^2+\frac{7}{... - Hoc24
Đúng 1
Bình luận (0)
Cho các số thực a,b,c thỏa mãn a+b+c/2=a+b-7/4c=b+c+3/4a=a+c+4=4b . Tính giá trị của biểu thức A=20a+11b+2017c
Câu hỏi của nguyen phuong thao - Toán lớp 7 - Học toán với OnlineMath
Các Ctv hoặc các giáo viên helpp ạ
Cho a,b,c là số thực dương không âm thỏa mãn
Cho a,b,c là số thực dương không âm thỏa mãn \(a+b+c=1\) . Chứng minh rằng :
\(\dfrac{1}{a^2+b^2}+\dfrac{1}{b^2+c^2}+\dfrac{1}{c^2+a^2}>10\)
Cho các số thực a,b,c thỏa mãn . Tính P a+ 2b+ 3c khi biểu thức
2
a
+
b
-
2
c
+
7
đạt giá trị lớn nhất A. P7 B. P3 C. P-3 D. P-7
Đọc tiếp
Cho các số thực a,b,c thỏa mãn . Tính P = a+ 2b+ 3c khi biểu thức 2 a + b - 2 c + 7 đạt giá trị lớn nhất
A. P=7
B. P=3
C. P=-3
D. P=-7
Đáp án B

Áp dụng bất đẳng thức giá trị tuyệt đối và bất đẳng thức BCS, ta có kết quả sau:
2 a + b - 2 c + 7 = 2 a + 1 + b - 2 - 2 c + 11 ≤ 2 a - 1 + b - 2 - 2 c + 11 ≤ a - 1 2 + b - 2 2 + c 2 2 2 + 1 2 + - 2 2 + 11 = 20
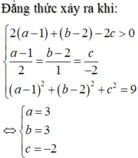
Cách 2: phương pháp hình học.
Trong không gian Oxyz, gọi mặt cầu (S) có tâm I(1;2;0), bán kính R=3. Khi đó:
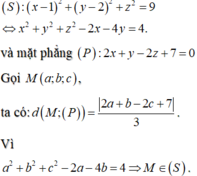
Bài toán đã cho trở thành:
Tìm M ∈ ( S ) sao cho d(M;(P)) lớn nhất
Gọi △ là đường thẳng qua I và vuông góc (P)

Phân tích: Khi quan sát 2 cách giải, đối với giáo viên ta sẽ dễ chọn Cách 1 vì ngắn gọn và tiết kiệm thời gian. Tuy nhiên học sinh không nhiều em đã từng được tiếp cận bất đẳng thức BCS. Đối với Cách 2, về mặt trình bày có thể dài hơi, nhiều tính toán hơn nhưng đó chỉ là những bước tính toán khá cơ bản, một học sinh khá nếu nhận ra ý đồ tác giả thì việc giải bài toán cũng không mất quá nhiều thời gian. Bài toán sẽ dễ hơn nếu đề bài chỉ yêu cầu tìm Min hoặc Max của biểu thức 2 a + b - 2 c + 7
Đúng 0
Bình luận (0)





