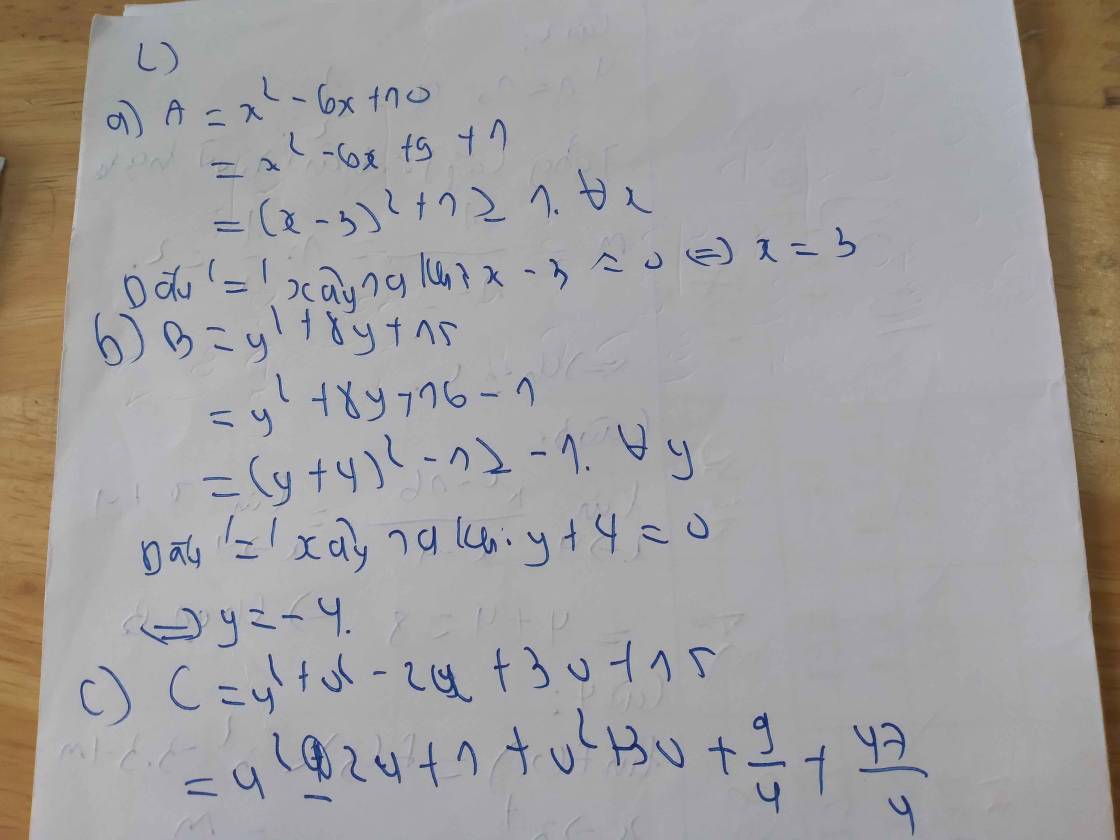Cho A, B, C là các tập hợp. Chứng minh rằng
A\B ⊂ C ⇔ A ⊂ B ∪ C.
H24
Những câu hỏi liên quan
Cho a, b, c, d là các số tự nhiên, a < b, c < d. Chứng minh rằng
a + c < b + d
NA
30 tháng 9 2021 lúc 16:21
Bài 1: Cho các tập hợp: A{1;2;3}, B{2;3;6;7}, C{3;4;5;8}a)Tìm AcapB, AcupB, AB, BAb)Chứng minh Acap(BC)(AcapB)AcapC)Bài 2: Cho A là một tập hợp tùy ý. Xác định các tập hợp sau:a)AcapA; AcupA; Acapvarnothing; Acupvarnothingb)AA; Avarnothing; varnothingA
Đọc tiếp
Bài 1: Cho các tập hợp: A={1;2;3}, B={2;3;6;7}, C={3;4;5;8}
a)Tìm A\(\cap\)B, A\(\cup\)B, A\B, B\A
b)Chứng minh A\(\cap\)(B\C)=(A\(\cap\)B)\(A\(\cap\)C)
Bài 2: Cho A là một tập hợp tùy ý. Xác định các tập hợp sau:
a)A\(\cap\)A; A\(\cup\)A; A\(\cap\)\(\varnothing\); A\(\cup\)\(\varnothing\)
b)A\A; A\\(\varnothing\); \(\varnothing\)\A
Dạng 4. Bài Tập Nâng Cao :
Bài 1 : Chứng minh rằng
a, A = 9c2 - 6c + 3 > 0, ∀ c. B = 14m - 6m2 - 13 < 0, ∀ m.
Bài 2. Tìm GTNN của các biểu thức sau
a, A = x2 - 6x + 10. b, B = y2 + 8y + 15.
c, C = u2 + v2 - 2u + 3v + 15 d, D = 2x2 + 5y2 + 4xy + 8x - 4y - 100.
Cho A,B,C là các tập khác rỗng. Chứng minh rằng nếu A hợp C bằng A hợp B và A giao C bằng A giao B thì B bằng C
DT
8 tháng 12 2021 lúc 14:52
cho \(\dfrac{a}{b}\)=\(\dfrac{c}{d}\). Chứng minh rằng
a) \(\dfrac{a}{b}\)=\(\dfrac{a+c}{b+d}\)
b) \(\dfrac{a+b}{a-b}\)=\(\dfrac{c+d}{c-d}\)
\(a,\dfrac{a}{b}=\dfrac{c}{d}=\dfrac{a+c}{b+d}\\ b,\dfrac{a}{b}=\dfrac{c}{d}\Leftrightarrow\dfrac{a}{c}=\dfrac{b}{d}=\dfrac{a+b}{c+d}=\dfrac{a-b}{c-d}\\ \Leftrightarrow\dfrac{a+b}{a-b}=\dfrac{c+d}{c-d}\)
Đúng 3
Bình luận (0)
Cho A,B,C là các tập tùy ý. Chứng minh rằng A trừ (B trừ C) bằng (A trừ B ) hợp ( A giao C)
Chứng minh các bất đẳng thức.
Cho a+b+c=o.chứng minh rằnga3+b3+c3=3abc
haizzz nhầm rồi mong các bạn hiểu là 3abc cho
Đúng 0
Bình luận (0)
Cho hai số hữu tỉ a/b và c/d (a,b,c,d thuộc z; b>0, d>0), trong đó a/b<c/d. Chứng minh rằng
a)a/d < b/c
b)a/b<a+c/b+d<c/d
Cho hai số hữu tỉ a/b và c/d (a,b,c,d thuộc z; b>0, d>0), trong đó a/b<c/d. Chứng minh rằng
a)a/d < b/c
b)a/b<a+c/b+d<c/d