P=1/y^2-xy+1/x^2-xy
biết xy=-1.Tính giá trị của bt
Tính giá trị của đa thức: x(1+y) - y(xy-1) - x2y. Biết x + y = -p; xy = q
1. a Tìm đa thức M, biết: M+ (x2y- 2xy2+xy+1) = x2y + xy2-xy-1\
b. Tính giá trị của đa thức M, biết x=1, y=2
a.M=3xy2-2xy-2
b.Thay x=1,y=2 vào đa thức M ta được:
M=3.1.22-2.1.2-2=12-4-2=6
BÀI 1: pttnt
a) x^3y-2x^y+xy b) x^2-9-4xy+y^2
bài 2 cho biểu thức 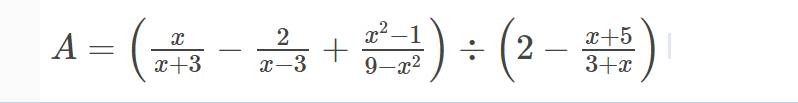
a) Tìm đk xác định của bt A
b) rút gọn bt A
c) tính giá trị của biểu thức A biết x^2-x-2=0
BÀI 1: pttnt
a) x^3y-2x^y+xy b) x^2-9-4xy+y^2
bài 2 cho biểu thức 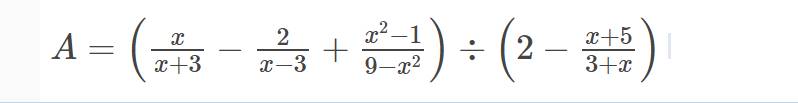
a) Tìm đk xác định của bt A
b) rút gọn bt A
c) tính giá trị của biểu thức A biết x^2-x-2=0
Bài 1:
a: Sửa đề \(x^3y-2x^2y+xy\)
\(=y\left(x^3-2x^2+x\right)\)
\(=x\cdot y\cdot\left(x^2-2x+1\right)\)
\(=xy\left(x-1\right)^2\)
b: Sửa đề: \(x^2-9-2xy+y^2\)
\(=\left(x^2-2xy+y^2\right)-9\)
\(=\left(x-y\right)^2-9\)
\(=\left(x-y-3\right)\left(x-y+3\right)\)
Bài 2:
a: ĐKXĐ: \(x\notin\left\{3;-3;-1\right\}\)
b: \(A=\left(\dfrac{x}{x+3}-\dfrac{2}{x-3}+\dfrac{x^2-1}{9-x^2}\right):\left(2-\dfrac{x+5}{x+3}\right)\)
\(=\left(\dfrac{x}{x+3}-\dfrac{2}{x-3}-\dfrac{x^2-1}{\left(x-3\right)\left(x+3\right)}\right):\dfrac{2x+6-x-5}{x+3}\)
\(=\dfrac{x\left(x-3\right)-2\left(x+3\right)-x^2+1}{\left(x+3\right)\left(x-3\right)}\cdot\dfrac{x+3}{x+1}\)
\(=\dfrac{x^2-3x-2x-6-x^2+1}{x-3}\cdot\dfrac{1}{x+1}\)
\(=\dfrac{-5x-5}{\left(x-3\right)\left(x+1\right)}=-\dfrac{5\left(x+1\right)}{\left(x-3\right)\left(x+1\right)}=-\dfrac{5}{x-3}\)
c: \(x^2-x-2=0\)
=>\(\left(x-2\right)\left(x+1\right)=0\)
=>\(\left[{}\begin{matrix}x-2=0\\x+1=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=2\left(nhận\right)\\x=-1\left(loại\right)\end{matrix}\right.\)
Thay x=2 vào A, ta được:
\(A=\dfrac{-5}{2-3}=\dfrac{-5}{-1}=5\)
tính giá trị của b=x(1+y)-y(xy-1)-x^2 tại x+y = -p, xy=q
\(\left\{{}\begin{matrix}S=x+y=-p\\P=xy=q\end{matrix}\right.\)
Nên \(x;y\) là nghiệm của phương trình
\(X^2-SX+P=0\)
\(\Leftrightarrow X^2+pX+q=0\)
\(\Leftrightarrow\left\{{}\begin{matrix}x=\dfrac{-p\pm\sqrt[]{p^2-4q}}{2}\\y=\dfrac{-p\mp\sqrt[]{p^2-4q}}{2}\end{matrix}\right.\left(1\right)\)
\(B=x\left(1+y\right)-y\left(xy-1\right)-x^2\)
\(\Leftrightarrow B=x+xy-xy^2+y-x^2\)
\(\Leftrightarrow B=x+y+xy-x\left(x+y\right)\)
\(\Leftrightarrow B=\left(x+y\right)\left(1-x\right)+xy\)
\(\Leftrightarrow B=-p\left(1-x\right)+q\)
\(\left(1\right)\Leftrightarrow B=-p\left[\left(1-\dfrac{-p\pm\sqrt[]{p^2-4q}}{2}\right)\right]+q\)
1) Tính giá trị của biểu thức sau
3/4 xy\(^2\)(x^2 +2/3xy+4/3y^2) - 1/2 xy(-1/2x^2y +xy^2+y^3) tai. x=1/2 ,y=2
rút gọn rồi tính giá trị biểu thức
a, I = x (y^2 - xy^2) + y (x^2y - yx = x) tại x = 3 và y =1/3
b, K = x^2 ( y^2 +xy^2 +1) - ( x^3 +x^2 +1 ) y^2 tại x = 0,5 và y = -1/2
tìm x bt
a, 2 ( 5x - 8 ) - 3 ( 4x - 5 ) = 4 ( 3x - 4 ) + 11
b, 2x ( 6x - 2x^2 ) + 3x^2 ( x - 4) = 8
Bài 2:
a: Ta có: \(2\left(5x-8\right)-3\left(4x-5\right)=4\left(3x-4\right)+11\)
\(\Leftrightarrow10x-16-12x+15=12x-16+11\)
\(\Leftrightarrow-14x=-4\)
hay \(x=\dfrac{2}{7}\)
b: Ta có: \(2x\left(6x-2x^2\right)+3x^2\left(x-4\right)=8\)
\(\Leftrightarrow12x^2-4x^3+3x^3-12x^2=8\)
\(\Leftrightarrow x^3=-8\)
hay x=-2
Bài 1:
a: Ta có: \(I=x\left(y^2-xy^2\right)+y\left(x^2y-xy+x\right)\)
\(=xy^2-x^2y^2+x^2y^2-xy^2+xy\)
\(=xy\)
=1
b: Ta có: \(K=x^2\left(y^2+xy^2+1\right)-\left(x^3+x^2+1\right)\cdot y^2\)
\(=x^2y^2+x^3y^2+x^2-x^3y^2-x^2y^2-y^2\)
\(=x^2-y^2\)
\(=\dfrac{1}{4}-\dfrac{1}{4}=0\)
Cho đa thức :A=1/2x^3y=x(xy^2)-1/2x. xy+x^2 2y^3+2x3y2
1) thu gọn A
2)tính giá trị của đa thức A biết x+y=5 và 1/x+1/y=-1
Cho x, y > 0 thỏa mãn xy ≤ y - 1. Tính giá trị nhỏ nhất của G = (x^2 + y^2)/xy