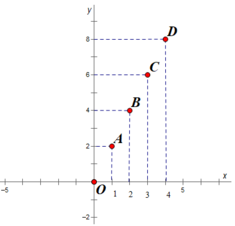
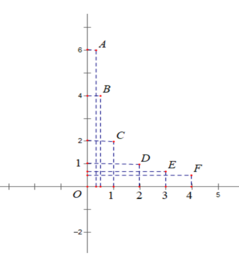
Bài 1: a. Biểu diễn các điểm sau trên hệ trục tọa độ Oxy:
A(4; 3); B(4; -2);C(-3; -2); D (0; -3); E(2; 0)
b.Biểu diễn trên hệ trục tọa độ Oxy các điểm có tung độ bằng 2.
c. Biểu diễn trên hệ trục tọa độ Oxy các điểm có hoành độ bằng 1.
Bài 2 : Cho hàm số y = -2x
a. Biết A(3; yo) thuộc đồ thị của hàm số y = -2x . Tính yo
b. Điểm B(1,5; 3) có thuộc đồ thị của hàm số y = -2x hay không? Tại sao?
c. Vẽ đồ thị hàm số y = -2x.
Bài 5 A và B là hai điểm thuộc đồ thị hàm số y = 3x + 1.
a. Tung độ của điểm A là bao nhiêu nếu hoành độ của nó bằng ![]() ?
?
b. Hoành độ của điểm B là bao nhiêu nếu tung độ của nó bằng -8?
c. Trong các điểm: C( -1;2) ; D( 2; 5); E( -2; 5), điểm nào thuộc đồ thị hàm số y = 3x + 1?
Bài 6 Xác định giá trị m, k biết:
a. Đồ thị hàm số y = 3x + m đi qua điểm (2; 7).
b. Đồ thị hàm số y = kx + 5 đi qua điểm (2; 11).
Bài 7 Cho hàm số y = f(x) = x2 – 8
a)Tính f(3) ; f(-2)
b)Tìm x khi biết giá trị của y là 17
Bài 8: Cho hàm số y = f(x) = 10 – x2
a)Tính f(-5) ; f(4)
b)Tìm x khi biết giá trị của y là 1