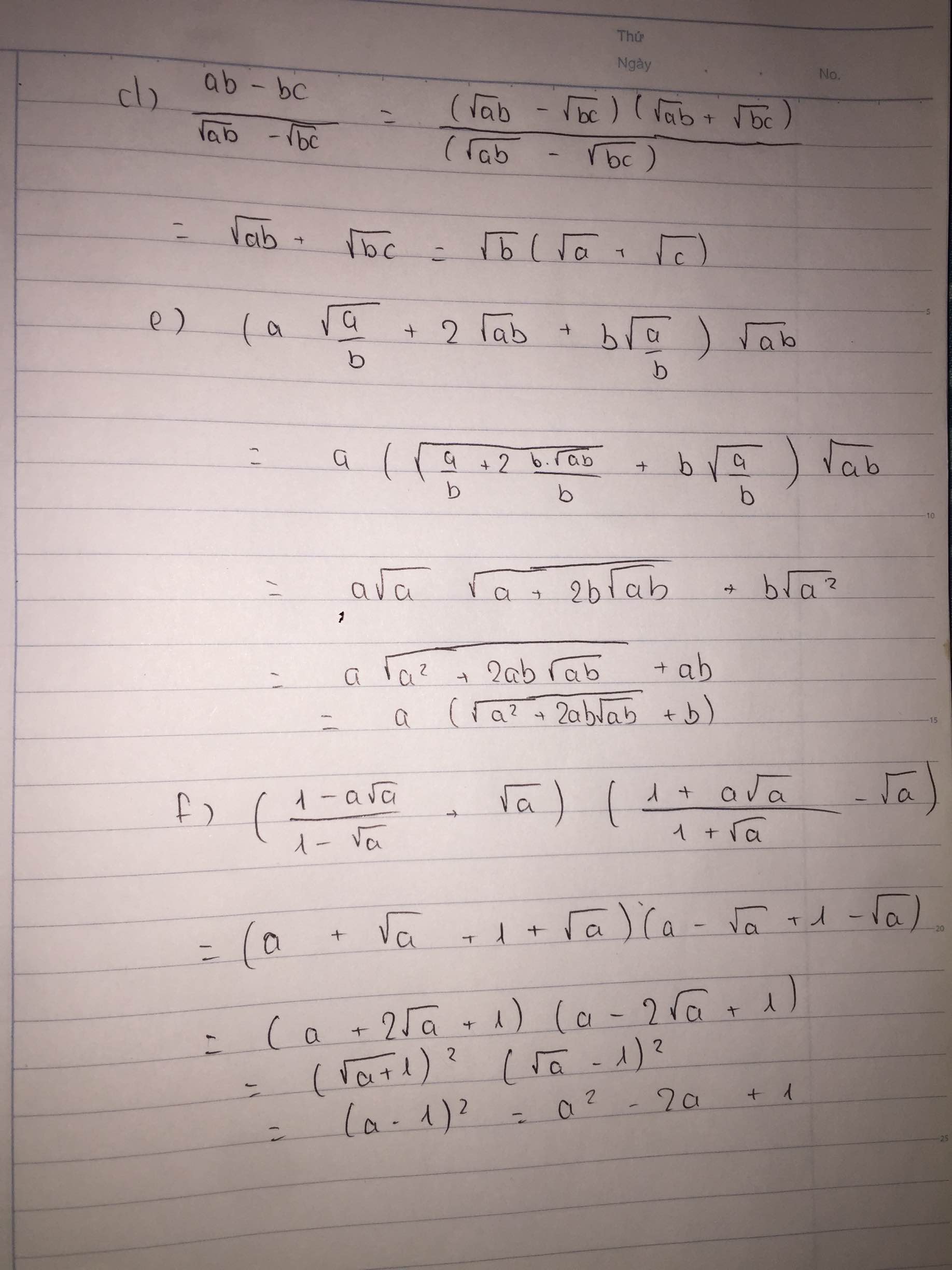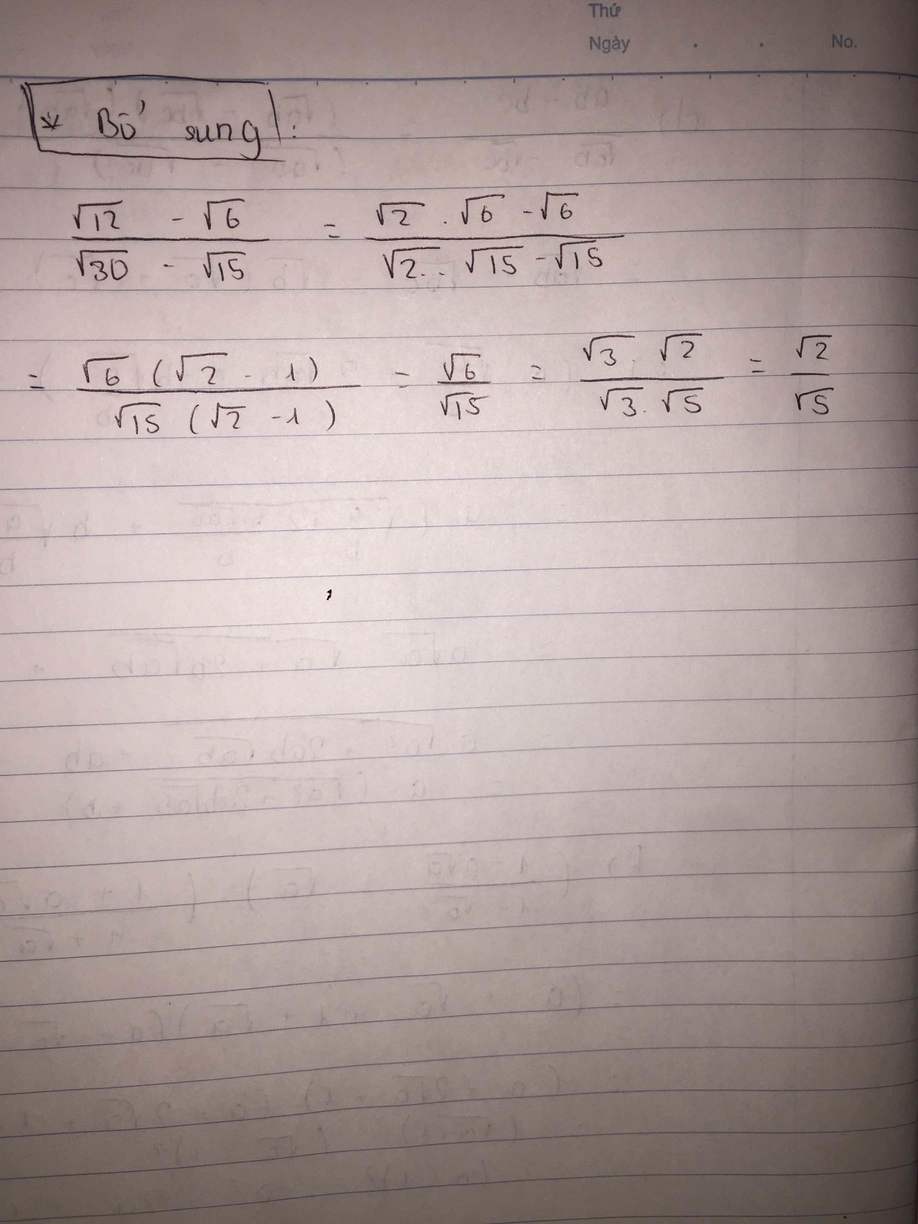giúp em hai câu e,f cuối với ạ 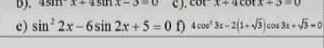
NC
Những câu hỏi liên quan

giải giúp em bài 13 với ạ
chỉ cần giải 4 ý cuối thôi ạ ( 2 ý e, hai ý f ạ)
Giúp em hai câu cuối với ạ !!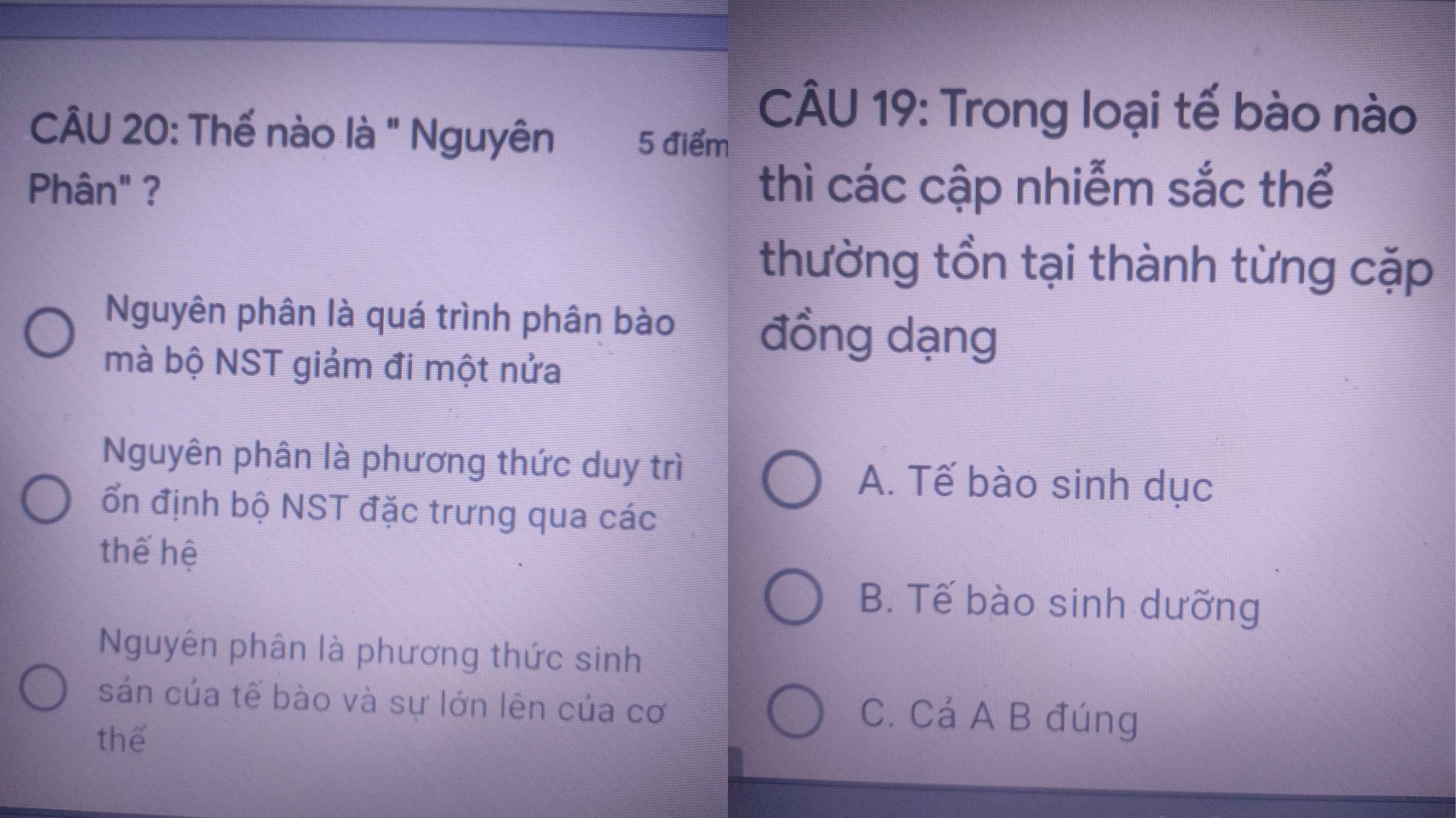
19B (tế bào sinh dục gồm: tb sinh dục sơ khai có bộ NST tồn tại thành từng cặp tương đồng; giao tử có bộ NST tồn tại thành từng chiếc đơn lẻ)
20C
Đúng 1
Bình luận (0)
Xem thêm câu trả lời
Giúp em bai 1 với câu e với f thôi ạ
 Giusp em với mọi người ạ. Rút gọn câu d, e, f, b giúp em với ạ, Em cảm ơn nhiều lắm.
Giusp em với mọi người ạ. Rút gọn câu d, e, f, b giúp em với ạ, Em cảm ơn nhiều lắm.
\(b,\dfrac{\sqrt{12}-\sqrt{6}}{\sqrt{30}-\sqrt{15}}=\dfrac{\sqrt{6}\left(\sqrt{2}-1\right)}{\sqrt{15}\left(\sqrt{2}-1\right)}=\dfrac{\sqrt{6}}{\sqrt{15}}=\dfrac{\sqrt{2}}{\sqrt{5}}\)
\(d,\dfrac{ab-bc}{\sqrt{ab}-\sqrt{bc}}=\dfrac{\left(\sqrt{ab}-\sqrt{bc}\right)\left(\sqrt{ab}+\sqrt{bc}\right)}{\left(\sqrt{ab}-\sqrt{bc}\right)}=\sqrt{ab}+\sqrt{bc}=\sqrt{b}\left(\sqrt{a}+\sqrt{c}\right)\)
\(e,\left(a\sqrt{\dfrac{a}{b}+2\sqrt{ab}}+b\sqrt{\dfrac{a}{b}}\right)\sqrt{ab}\)
\(=a\left(\sqrt{\dfrac{a}{b}+\dfrac{2b.\sqrt{ab}}{b}}+b\sqrt{\dfrac{a}{b}}\right)\sqrt{ab}\)
\(=a\sqrt{a}\sqrt{a+2b\sqrt{ab}}+b\sqrt{a^2}\)
\(=a\sqrt{a^2+2ab\sqrt{ab}}+ab\)
\(=a\left(\sqrt{a^2+2ab\sqrt{ab}}+b\right)\)
\(f,\left(\dfrac{1-a\sqrt{a}}{1-\sqrt{a}}+\sqrt{a}\right)\left(\dfrac{1+a\sqrt{a}}{1+\sqrt{a}}-\sqrt{a}\right)\)
\(=\left(a+\sqrt{a}+1+\sqrt{a}\right)\left(a-\sqrt{a}+1-\sqrt{a}\right)\)
\(=\left(a+2\sqrt{a}+1\right)\left(a-2\sqrt{a}+1\right)\)
\(=\left(\sqrt{a}+1\right)^2\left(\sqrt{a}-1\right)^2\)
\(=\left(a-1\right)^2=a^2-2a+1\)
Đúng 1
Bình luận (0)
Giải giúp em câu bcdef với ạ riêng b,e,f giải đưa về cos giúp em
b.
\(\Leftrightarrow\dfrac{1}{2}cosx-\dfrac{\sqrt{3}}{2}sinx=-\dfrac{1}{2}\)
\(\Leftrightarrow cos\left(x+\dfrac{\pi}{3}\right)=-\dfrac{1}{2}\)
\(\Leftrightarrow\left[{}\begin{matrix}x+\dfrac{\pi}{3}=\dfrac{2\pi}{3}+k2\pi\\x+\dfrac{\pi}{3}=-\dfrac{2\pi}{3}+k2\pi\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{\pi}{3}+k2\pi\\x=-\pi+k2\pi\end{matrix}\right.\)
Đúng 1
Bình luận (0)
c.
\(\Leftrightarrow\dfrac{3}{5}sinx-\dfrac{4}{5}cosx=1\)
Đặt \(\dfrac{3}{5}=cosa\) với \(a\in\left(0;\dfrac{\pi}{2}\right)\Rightarrow\dfrac{4}{5}=sina\)
Pt trở thành:
\(sinx.cosa-cosx.sina=1\)
\(\Leftrightarrow sin\left(x-a\right)=1\)
\(\Leftrightarrow x-a=\dfrac{\pi}{2}+k2\pi\)
\(\Leftrightarrow x=a+\dfrac{\pi}{2}+k2\pi\)
Đúng 1
Bình luận (0)
d.
\(\Leftrightarrow\dfrac{\sqrt{2}}{2}sinx-\dfrac{\sqrt{2}}{2}cosx=\dfrac{\sqrt{2}}{2}\)
\(\Leftrightarrow sin\left(x-\dfrac{\pi}{4}\right)=\dfrac{\sqrt{2}}{2}\)
\(\Leftrightarrow\left[{}\begin{matrix}x-\dfrac{\pi}{4}=\dfrac{\pi}{4}+k2\pi\\x-\dfrac{\pi}{4}=\dfrac{3\pi}{4}+k2\pi\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{\pi}{2}+k2\pi\\x=\pi+k2\pi\end{matrix}\right.\)
Đúng 1
Bình luận (0)
Xem thêm câu trả lời
Moị người giúp em bài 1 câu d,e,f với ạ
mọi ng giải giúp em câu e,f bài 1 với ạ
e:
\(E=\left(\dfrac{\sqrt{15}-\sqrt{20}}{2-\sqrt{3}}+\dfrac{\sqrt{21}-\sqrt{7}}{1-\sqrt{3}}\right):\dfrac{1}{\sqrt{7}-\sqrt{5}}\)
\(=\left(-\dfrac{\sqrt{5}\left(2-\sqrt{3}\right)}{2-\sqrt{3}}-\dfrac{\sqrt{7}\left(1-\sqrt{3}\right)}{1-\sqrt{3}}\right)\cdot\dfrac{\sqrt{7}-\sqrt{5}}{1}\)
\(=-\left(\sqrt{7}+\sqrt{5}\right)\left(\sqrt{7}-\sqrt{5}\right)\)
=-2
f: \(F=\sqrt{3}+1+2-\sqrt{3}=3\)
Đúng 2
Bình luận (0)
Đề bài đâu rồi em?
Đúng 2
Bình luận (1)
Trong bài thơ "Tụng giá hoàn kinh sư", em hãy tìm và giải nghĩa một từ ghép Hán Việt có trong hai câu thơ cuối bài thơ.
mn giúp e nhanh với ạ, e xin cảm ơn ><