Tính Độ dài các cạnh góc vuông của tam giác vuông cân có cạnh huyền bằng
a) 2cm
b)\(\sqrt{2cm}\)
Tính độ dài các cạnh góc vuông của một tam giác vuông cân,biết độ dài cạnh huyền là:
a)2cm
b)\(\sqrt{2cm}\)
a: Gọi độ dài cạnh góc vuông là x
Theo đề, ta có: \(2x^2=4\)
hay \(x=\sqrt{2}\left(cm\right)\)
b: Gọi độ dài cạnh góc vuông là x
Theo đề, ta có: \(2x^2=2\)
hay x=1(cm)
Tính độ dài các cạnh góc vuông của một tam giác vuông cân có độ dài cạnh huyền bằng:
a) 2cm
b) 2 cm
Tính độ dài các cạnh góc vuông của một tam giác vuông cân có độ dài cạnh huyền bằng :
a, 2cm
b, căn bậc 2 cm
Cạnh huyền của một tam giác vuông bằng 10cm. Hai cạnh góc vuông có độ dài hơn kém nhau 2cm. Tính độ dài các cạnh góc vuông của tam giác vuông đó.
Gọi số đo độ dài hai cạnh góc vuông của tam giác vuông đó là x(cm), y (cm)
( 0 < y < x < 10)
Hai cạnh góc vuông có độ dài hơn kém nhau 2cm nên ta được x – y = 2 , (1).
Theo định lý Pytago ta có: x 2 + y 2 = 10 2 = 100 ( 2 )
Từ (1) và (2) ta có hệ phương trình:
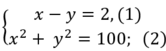
Từ (1) suy ra: x= y+ 2 thay vào (2) ta được:
( y + 2 ) 2 + y 2 = 100 ⇔ y 2 + 4 y + 4 + y 2 = 100 ⇔ 2 y 2 + 4 y − 96 = 0 hay y 2 + 2 y − 48 = 0
Giải ra ta được: y 1 = 6 ; y 2 = - 8 < 0 ( loại)
Với y= 6 suy ra x = 8.
Vậy độ dài các cạnh góc vuông của tam giác vuông là 6cm và 8cm.
Cạnh huyền của một tam giác vuông bằng 10cm. Hai cạnh góc vuông có độ dài hơn kém nhau 2cm. Tính độ dài các cạnh góc vuông của tam giác vuông đó.
Gọi số đo độ dài hai cạnh góc vuông của tam giác vuông đó là x(cm), y (cm)
( 0 < y < x < 10)
Hai cạnh góc vuông có độ dài hơn kém nhau 2cm nên ta được x – y = 2 , (1).
Theo định lý Pytago ta có: x 2 + y 2 = 10 2 = 100 ( 2 )
Từ (1) và (2) ta có hệ phương trình:
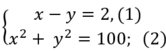
Từ (1) suy ra: x= y+ 2 thay vào (2) ta được:
( y + 2 ) 2 + y 2 = 100 ⇔ y 2 + 4 y + 4 + y 2 = 100
⇔ 2 y 2 + 4 y – 96 = 0 h a y y 2 + 2 y – 48 = 0
Giải ra ta được: y 1 = 6 ; y 2 = - 8 < 0 ( l o ạ i )
Với y= 6 suy ra x = 8.
Vậy độ dài các cạnh góc vuông của tam giác vuông là 6cm và 8cm.
Tính độ dài các cạnh góc vuông của một tam giác vuông cân có cạnh huyền bằng :
a) \(2cm\)
b) \(\sqrt{2}cm\)
a) Gọi \(\Delta\)ABC vuông cân tại A có BC = 2 cm
Áp dụng định lý Pytago cho \(\Delta\)ABC vuông cân tại A ta có :
AB2 + AC2 = BC2
AB2 + AB2 = 2 ( Vì AB = AC)
2.AB2 = 4
=> AB2 = 2
=> AB = \(\sqrt{2}\)
Vậy AB = AC = \(\sqrt{2}\)(cm)
b) Gọi \(\Delta\)KFC vuông cân tại K có FC = \(\sqrt{2}\)(cm)
Áp dụng định lý Pytago cho \(\Delta\)KFC vuông cân tại K ta có :
FC2 = KF2 + KC2
(\(\sqrt{2}\))2 = 2. KF2 (vì KC = KF)
=> 2 = 2 . KF2
=> KF2 = 1
=> KF = 1 (cm)
Vậy KC = KF = 1 (cm)
Cạnh huyền của một tam giác vuông bằng 10. Hai cạnh góc vuông có độ dài hơn kém nhau 2cm. Tính độ dài các cạnh góc vuông của tam giác vuông đó ?
gọi 2 canh tam giác là x và x+2
áp dụng định lí pytago ta có
x^2+(x+2)^2=10^2
suy ra x^2+x^2+4x+4=100
suy ra x=6 (vì x>0)
suy ra2 cạnh góc vuông là 6 và 8cm
Gọi x là độ dài một cạnh hình vuông
độ dài cạnh còn lại là x- 2
theo đề ta có pt
x^2+(x-2)^2=10^2
<=>x^2+x^2- 4x+ 4 -100= 0
<=>2x^2 -4x -96= 0
\(\Delta\)'= (-2)^2 -2×(-96)= 196 > 0
x1 =8 (nhận)
x2= -6 (loại)
vậy cạnh của hình vuông là 8;6
Tính độ dài các cạnh góc vuông của một tam giác vuông cân có cạnh huyền bằng:
a) 2cm
b / 2cm
/ là căn 2 nha mấy bạ
goi canh goc vuong la X cm
su dung dinh li ptg
a)
22=x2+x2=2x2
giai pt ta duoc X=can 2 cm
b)
(can 2)2= x2+x2
giai pt ta duoc X=1cm
cạnh bé nhất của 1 tam giác vuông có độ dài =6cm,cạnh huyền có độ dài lớn hơn cạnh góc vuông còn lại 2cm. tính độ dai cạnh huyền của tam giác vuông đó