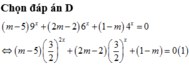CMR phương trình : \(x^3+6x^2+9x+1=0\) có ba nghiệm phân biệt
NT
Những câu hỏi liên quan
Có bao nhiêu giá trị nguyên của tham số m để phương trình
(
m
-
5
)
9
x
+
(
2
m
-
2
)
6
x
+
(
1
-
m
)
4
x
0
có hai nghiệm phân biệt? A. 2 B. 4 C. 3 D. 1
Đọc tiếp
Có bao nhiêu giá trị nguyên của tham số m để phương trình ( m - 5 ) 9 x + ( 2 m - 2 ) 6 x + ( 1 - m ) 4 x = 0 có hai nghiệm phân biệt?
A. 2
B. 4
C. 3
D. 1
Biết rằng phương trình
a
x
3
+
21
x
2
+
6
x
+
2019
0
có ba nghiệm thực phân biệt (a là tham số). Phương trình
4
a
x
3
+
21
x
2
+...
Đọc tiếp
Biết rằng phương trình a x 3 + 21 x 2 + 6 x + 2019 = 0 có ba nghiệm thực phân biệt (a là tham số). Phương trình 4 a x 3 + 21 x 2 + 6 x + 2019 3 a x + 21 = 9 a x 2 + 14 x + 2 2 có bao nhiêu nghiệm thực phân biệt?
A. 1
B. 4
C. 2
D. 3
Chọn đáp án C.
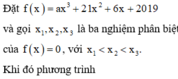
4 a x 3 + 21 x 2 + 6 x + 2019 3 a x + 21 = 9 a x 2 + 14 x + 2 2
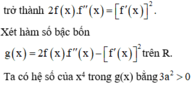
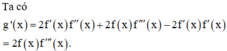
Vì f(x) = 0 có ba nghiệm phân biệt nên a ≠ 0
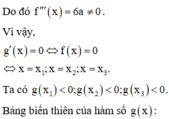
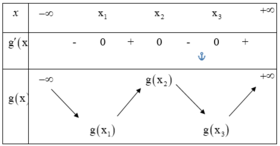
Từ bảng biến thiên, ta thấy phương trình g(x) = 0 có đúng hại nghiệm phân biệt.
Do đó phương trình 4 a x 3 + 21 x 2 + 6 x + 2019 3 a x + 21 = 9 a x 2 + 14 x + 2 2 có đúng hai nghiệm phân biệt.
Đúng 0
Bình luận (0)
Hỏi phương trình 3x2- 6x+ ln( x+1) 3+1=0 có bao nhiêu nghiệm phân biệt?
A. 2.
B. 1.
C. 3.
D. 4.
Điều kiện: x> -1
Ta có: 3x2- 6x+ ln( x+1) 3+1=0 hay 3x2- 6x+ 3ln( x+1)+1=0
f(x)=3x2- 6x+ 3ln( x+1) +1=0 ⇒ f ' ( x ) = 6 x - 6 + 3 x + 1
Đạo hàm f’ (x) = 0 khi và chỉ khi (2x- 2) (x+ 1) +1=0
⇔ x = ± 1 2
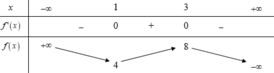
Từ đây, ta có bảng biến thiên của f(x):
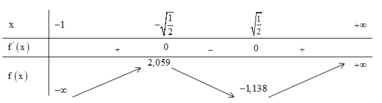
Nhìn vào bảng biến thiên ta sẽ có phương trình đã cho có 3 nghiệm phân biệt.
Chọn C.
Đúng 0
Bình luận (0)
cho pt: \(x^3-x^2+2mx-2m=0\left(1\right)\)
a, Tìm m để phương trình có ba nghiệm phân biệt x1,x2,x3 tm: x1+x2+x3=10
b,Tìm m để phương trình có ba nghiệm phân biệt đều lớn hơn hoặc bằng 1.
\(x^3-x^2+2mx-2m=0\)
\(\Leftrightarrow x^2\left(x-1\right)+2m\left(x-1\right)=0\)
\(\Leftrightarrow\left(x-1\right)\left(x^2+2m\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=1\\x^2=-2m\end{matrix}\right.\)
Để pt có 3 nghiệm \(\Rightarrow-2m>0\Rightarrow m< 0\)
a. Do vai trò 3 nghiệm như nhau, ko mất tính tổng quát giả sử \(x_1=1\) và \(x_2;x_3\) là nghiệm của \(x^2+2m=0\)
Để pt có 3 nghiệm pb \(\Rightarrow\left\{{}\begin{matrix}-2m>0\\-2m\ne1\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}m< 0\\m\ne-\dfrac{1}{2}\end{matrix}\right.\)
Khi đó: \(x_2+x_3=0\Rightarrow x_1+x_2+x_3=1\ne10\) với mọi m
\(\Rightarrow\) Không tồn tại m thỏa mãn yêu cầu
b.
Giả sử pt có 3 nghiệm, khi đó \(\left[{}\begin{matrix}x_2=-\sqrt{-2m}< 0< 1\\x_3=\sqrt{-2m}\end{matrix}\right.\)
\(\Rightarrow\) Luôn có 1 nghiệm của pt âm \(\Rightarrow\) không tồn tại m thỏa mãn
Em coi lại đề bài
Đúng 2
Bình luận (0)
cho P(x)=x^3+ax^2+bx+c; Q(x)=x^2+x+2013. Biết phương trình P(x)=0 có 3 nghiệm phân biệt, còn phương trình P(Q(x))=0 vô nghiệm. CMR: P(2013)>1/64
+) Ta có: P(x) = 0 có 3 nghiệm phân biệt
=> Gọi 3 nghiệm đó là m; n ; p.
=> P(x) = ( x - m ) ( x - p ) (x - n)
=> P(Q(x)) = ( x^2 + x + 2013 -m )( x^2 + x + 2013 -n )( x^2 + x + 2013 - p )
Vì P(Q(x)) =0 vô nghiệm nên: x^2 + x + 2013 - m = 0 ;x^2 + x + 2013 - m = 0; x^2 + x + 2013 - m = 0 đều vô nghiệm
=> \(\Delta_m=1^2-4\left(2013-m\right)< 0;\Delta_n=1^2-4\left(2013-n\right)< 0;\Delta_p=1^2-4\left(2013-p\right)< 0\)
=> \(2013-m>\frac{1}{4};2013-n>\frac{1}{4};2013-p>\frac{1}{4}\)
=> P(2013) = ( 2013 - m) (2013 -n ) (2013 - p) >\(\frac{1}{4}.\frac{1}{4}.\frac{1}{4}=\frac{1}{64}\)
1. Chứng minh phương trình left(m^2+1right)x^3-2m^2x^2-4x+m^2+10 có đúng 3 nghiệm phân biệt.2. Cho phương trình :x^3cos^3x+mleft(x.cosx-1right)left(x.cosx+2right)0 CMR phương trình luôn có nghiệm với mọi m3. Cho phương trình left(m^2-m+2021right)x^3-left(2m^2-2n+4040right)x^2-4x+m^2-m+20210CMR phương trình có 3 nghiệm phân biệt với mọi giá trị của tham số m
Đọc tiếp
1. Chứng minh phương trình
\(\left(m^2+1\right)x^3-2m^2x^2-4x+m^2+1=0\) có đúng 3 nghiệm phân biệt.
2. Cho phương trình :
\(x^3cos^3x+m\left(x.cosx-1\right)\left(x.cosx+2\right)=0\)
CMR phương trình luôn có nghiệm với mọi m
3. Cho phương trình
\(\left(m^2-m+2021\right)x^3-\left(2m^2-2n+4040\right)x^2-4x+m^2-m+2021=0\)
CMR phương trình có 3 nghiệm phân biệt với mọi giá trị của tham số m
1.
Đặt \(f\left(x\right)=\left(m^2+1\right)x^3-2m^2x^2-4x+m^2+1\)
\(f\left(x\right)\) xác định và liên tục trên R
\(f\left(x\right)\) có bậc 3 nên có tối đa 3 nghiệm (1)
\(f\left(0\right)=m^2+1>0\) ; \(\forall m\)
\(f\left(1\right)=\left(m^2+1\right)-2m^2-4+m^2+1=-2< 0\) ;\(\forall m\)
\(\Rightarrow f\left(0\right).f\left(1\right)< 0\Rightarrow f\left(x\right)\) luôn có ít nhất 1 nghiệm thuộc \(\left(0;1\right)\) (2)
\(f\left(2\right)=8\left(m^2+1\right)-8m^2-8+m^2+1=m^2+1>0\)
\(\Rightarrow f\left(1\right).f\left(2\right)< 0\Rightarrow f\left(x\right)\) luôn có ít nhất 1 nghiệm thuộc \(\left(1;2\right)\) (3)
\(f\left(-3\right)==-27\left(m^2+1\right)-18m^2+12+m^2+1=-44m^2-14< 0\)
\(\Rightarrow f\left(-3\right).f\left(0\right)< 0\Rightarrow f\left(x\right)\) luôn có ít nhất 1 nghiệm thuộc \(\left(-3;0\right)\) (4)
Từ (1); (2); (3); (4) \(\Rightarrow f\left(x\right)=0\) có đúng 3 nghiệm phân biệt
Đúng 2
Bình luận (0)
2.
Đặt \(t=g\left(x\right)=x.cosx\)
\(g\left(x\right)\) liên tục trên R và có miền giá trị bằng R \(\Rightarrow t\in\left(-\infty;+\infty\right)\)
\(f\left(t\right)=t^3+m\left(t-1\right)\left(t+2\right)\)
Hàm \(f\left(t\right)\) xác định và liên tục trên R
\(f\left(1\right)=1>0\)
\(f\left(-2\right)=-8< 0\)
\(\Rightarrow f\left(1\right).f\left(-2\right)< 0\Rightarrow f\left(t\right)=0\) luôn có ít nhất 1 nghiệm thuộc \(\left(-2;1\right)\)
\(\Rightarrow f\left(x\right)=0\) luôn có nghiệm với mọi m
Đúng 2
Bình luận (0)
3. Chắc ngoặc thứ là \(\left(2m^2-2m+4040\right)\) ?
\(\Leftrightarrow\left(m^2-m+2021\right)x^3-2\left(m^2-m+2020\right)x^2-4x+m^2-m+2021=0\)
Do \(m^2-m+2020>0\), đặt \(m^2-m+2020=n^2\)
\(\Rightarrow\left(n^2+1\right)x^3-2n^2x^2-4x+n^2+1=0\)
Quy về bài số 1
Đúng 1
Bình luận (0)
Tìm m để phương trình
x
3
−
3
x
2
−
9
x
+
m
0
(1) có ba nghiệm phân biệt lập thành cấp số cộng. A. m 10 B. m 11 C. m 12 D. m 9
Đọc tiếp
Tìm m để phương trình x 3 − 3 x 2 − 9 x + m = 0 (1) có ba nghiệm phân biệt lập thành cấp số cộng.
A. m = 10
B. m = 11
C. m = 12
D. m = 9
Đáp án A
Điều kiện cần: Giả sử phương trình có ba nghiệm phân biệt lập thành cấp số cộng, khi đó
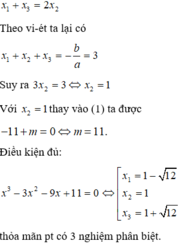
Đúng 0
Bình luận (0)
Phương trình
2
x
-
2
+
m
-
3
x
3
+
x
3
-
6
x
+
9
x
+...
Đọc tiếp
Phương trình 2 x - 2 + m - 3 x 3 + x 3 - 6 x + 9 x + m = 2 x + 1 + 1 có 3 nghiệm phân biệt khi và chỉ khi m ∈ ( a ; b ) . Đặt T = b 2 - a 2 thì
A. T=36
B. T=48
C. T=64
D. T=72
1) \(2x-x^2-\sqrt{6x^2-12x+7}=0\)
2) cho phương trình x2 - 2(m+1)x+m2+3=0 .Xác định m để phương trình có 2 nghiệm phân biệt x1 ,x2 thoả \(x_1^2+x_2^2=2x_1x_2+8\)
1.
\(\Leftrightarrow6x^2-12x+7-6\sqrt{6x^2-12x+7}-7=0\)
Đặt \(\sqrt{6x^2-12x+7}=t>0\)
\(\Rightarrow t^2-6t-7=0\Rightarrow\left[{}\begin{matrix}t=-1\left(loại\right)\\t=7\end{matrix}\right.\)
\(\Leftrightarrow\sqrt{6x^2-12x+7}=7\)
\(\Leftrightarrow6x^2-12x+7=49\Rightarrow x=1\pm2\sqrt{2}\)
2.
\(\Delta'=\left(m+1\right)^2-m^2-3=2m-2>0\Rightarrow m>1\)
Theo hệ thức Viet: \(\left\{{}\begin{matrix}x_1+x_2=2\left(m+1\right)\\x_1x_2=m^2+3\end{matrix}\right.\)
\(\left(x_1+x_2\right)^2-2x_1x_2=2x_1x_2+8\)
\(\Leftrightarrow\left(x_1+x_2\right)^2-4x_1x_2-8=0\)
\(\Leftrightarrow4\left(m+1\right)^2-4\left(m^2+3\right)-8=0\)
\(\Leftrightarrow2m-4=0\Rightarrow m=2\)
Đúng 1
Bình luận (0)