Cho tam giác MNP có MN = 5 cm ,NP = 4 cm, MP 3cm. Tam giác MNP là tam giác gì vì sao
TN
Những câu hỏi liên quan
Cho tam giác MNP có MP=6cm, MN=10cm, NP=8cm. Tam giác MNP là tam giác gì? Vì sao?
Giúp mik vs ạ!
Ta có: \(MP^2+NP^2=6^2+8^2=100\)
\(MN^2=10^2=100\)
Do đó: \(MP^2+NP^2=MN^2\)(=100)
Xét ΔMNP có \(MP^2+NP^2=MN^2\)(cmt)
nên ΔMNP vuông tại N(Định lí Pytago đảo)
Đúng 3
Bình luận (0)
Ko còn cái j ngoài cm hả có vuông góc ko?????
Đúng 1
Bình luận (0)
Cho tam giác MNP có \(MN = 4\)cm, \(NP = 5\)cm, \(MP = 6\) cm. Tìm góc nhỏ nhất, góc lớn nhất của tam giác MNP.
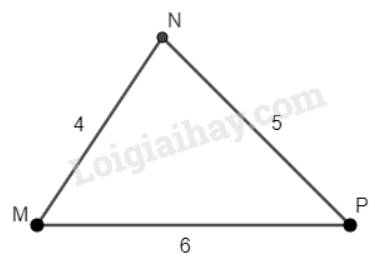
Trong tam giác MNP: \(MN < NP < MP\).
\(\Rightarrow\) Cạnh MN nhỏ nhất, MP lớn nhất trong tam giác MNP.
Vậy góc nhỏ nhất của tam giác MNP là góc P (đối diện với cạnh MN), góc lớn nhất của tam giác MNP là góc N (đối diện với cạnh MP)
Đúng 0
Bình luận (0)
Cho tam giác MNP có MN=10,MP=15cm. trên các cạnh MN và MP lấy các điểm H và K Sao cho MH=2,MK=3cm chứng minh a) Tam giác MHK Đồng dạng với tam giác MNP b) từ K kẻ KQ//MN (Q thuộc NP).Tứ giác NHKQ là hình gì vì sao. chứng minh tam giác PKQ Đồng dạng với tam giác KMH c)Tính NQ,QP biết NP=12cm
cho tam giác MNP có MN = 5 cm, NP=12cm ,MP=13cm chứng minh tam giác MNP vuông
Ta có:
+ MP2 = 132= 169
+ MN2+NP2= 52+122= 25+144=169
=> MP2 = MN2+NP2 (169=169)
Vậy tam giác MNP vuông tại N (Pytago đảo)
Đúng 0
Bình luận (0)
Áp dụng định lí Pytago cho tam giác MNP ta có :
MN2 + NP2 = 52 + 122 = 25 + 144 = 169
MP2 = 132 = 169
=> MP2 = MN2 + NP2
=> Tam giác MNP vuông ( đpcm )
Xem thêm câu trả lời
cho tam giác MNP có MN = 8 cm B = 16 cm trên cạnh MB lấy điểm E sao cho me = 4 cm đường phân giác MD của tam giác MNP cắt NE tại I (D thuộc NP)
a) Chứng minh tam giác MEN và tam giác MNP đồng dạng
b)cho MP = 20 cm Tính độ dài NE và độ dài DPDN
c)Chứng minh IE.DP= IN.DN
cho tam giác MNP vuông tại M . MN = 4cm, MP = 3cm. đường cao MI : a) Cm tam giác MNP và tam giác INM đồng dang => MN mũ 2 = NP . NI; b) tính độ dài NI và IP : c) gọi NE là tia phân giác của góc MNP . K là giao điểm NE và MI. cm EM/EP, NI/MN ; d) kẻ IH vuong góc với MN tại H. tính diện tích tam giác IMH
Cho tam giác MNP có cạnh MN = 2,4 cm, NP = 4 cm, MP = 3,2.
a/ Cm tam giác MNP là tam giác vuông.
b/ Gọi G là trung điểm cạnh MN, H là trung điểm cạnh MP. Tính độ dài đoạn thẳng GH.
Cho tam giác MNP có cạnh MN = 2,4 cm, NP = 4 cm, MP = 3,2.
a/ Cm tam giác MNP là tam giác vuông.
b/ Gọi G là trung điểm cạnh MN, H là trung điểm cạnh MP. Tính độ dài đoạn thẳng GH.
cho tam giác MNP có MN < MP . Kẻ tia phân giác MK của NMP ( K thuộc NP ) . Trên cạnh MP lấy điểm E sao cho ME = MN , trên tia MN lấy điểm F sao cho MF = MP
a) Cm Tam giác NMK = Tam giác EMK
b) Cm KF = KP
c) Cm Tam giác FKN = Tam giác PKE
d) CM ba điểm F ; K ; E thẳng hàng
a: Xét ΔMNK và ΔMEK có
MN=ME
góc NMK=góc EMK
MK chung
=>ΔMNK=ΔMEK
b,c: Xét ΔKNF và ΔKEP có
KN=KE
góc KNF=góc KEP
NF=EP
=>ΔKNF=ΔKEP
=>KF=KP
d: ΔKNF=ΔKEP
=>góc NKF=góc EKP
=>góc EKP+góc PKF=180 độ
=>F,K,E thẳng hàng
Đúng 0
Bình luận (0)
1. Cho tam giác MNP cân tại M vẽ MH thuộc NP (H thuộc NP)a) Chứng minh NH PHb) Cho MH 4 cm; NH 3 cm. Tính MN2. Cho tam giác MNP vuông tại M, có góc N 60o và MN 5 cm. Tia phân giác của góc N cắt MP tại D. Kẻ DE vuông góc với PN tại Ea) Chứng minh: tam giác MNP tam giác ENDb) Chứng minh: tam giác MNE là tam giác đềuc) Tính độ dài cạnh PN3. Cho tam giác MNP cân tại M, góc M 30o; NP 2 cm. Trên cạnh MP lấy điểm Q sao cho góc PNQ 60o. Tính độ dài MQ
Đọc tiếp
1. Cho tam giác MNP cân tại M vẽ MH thuộc NP (H thuộc NP)
a) Chứng minh NH = PH
b) Cho MH = 4 cm; NH = 3 cm. Tính MN
2. Cho tam giác MNP vuông tại M, có góc N = 60o và MN = 5 cm. Tia phân giác của góc N cắt MP tại D. Kẻ DE vuông góc với PN tại E
a) Chứng minh: tam giác MNP = tam giác END
b) Chứng minh: tam giác MNE là tam giác đều
c) Tính độ dài cạnh PN
3. Cho tam giác MNP cân tại M, góc M = 30o; NP = 2 cm. Trên cạnh MP lấy điểm Q sao cho góc PNQ = 60o. Tính độ dài MQ