Tính đạo hàm của hàm số y = cos2x . căn bậc hai của ( pi/4 - 2x)
Tính đạo hàm của hàm số \(y = 2\cos \left( {\frac{\pi }{4} - 2x} \right).\)
\(y'=-2\left(\dfrac{\pi}{4}-2x\right)'sin\left(\dfrac{\pi}{4}-2x\right)\\ =4sin\left(\dfrac{\pi}{4}-2x\right)\)
a) Gọi \(g\left( x \right)\) có đạo hàm của hàm số \(y = \sin \left( {2x + \frac{\pi }{4}} \right).\) Tìm \(g\left( x \right)\).
b) Tính đạo hàm của hàm số \(y = g\left( x \right)\).
a) \(g'\left( x \right) = y' = {\left( {2x + \frac{\pi }{4}} \right)^,}.\cos \left( {2x + \frac{\pi }{4}} \right) = 2\cos \left( {2x + \frac{\pi }{4}} \right)\)
b) \(g'\left( x \right) = - 2{\left( {2x + \frac{\pi }{4}} \right)^,}.\sin \left( {2x + \frac{\pi }{4}} \right) = - 4\sin \left( {2x + \frac{\pi }{4}} \right)\)
Tính đạo hàm cấp hai của các hàm số sau: y = cos 2 x
Tính đạo hàm cấp hai của hàm số sau y = sin5x. cos2x
A. y ' ' = 1 2 - 49 sin 7 x + 9 sin 3 x
B. y ' ' = - 1 2 49 sin 7 x + 9 sin 3 x
C. y ' ' = 1 2 49 sin 7 x - 9 sin 3 x
D. Đáp án khác
y ' = 2 2 − 3 x 2 x + 1 . 2 − 3 x 2 x + 1 ' = 2 2 − 3 x 2 x + 1 . − 3 2 x + 1 − 2 2 − 3 x 2 x + 1 2 = 2 2 − 3 x 2 x + 1 . − 7 2 x + 1 2 = − 14 2 x + 1 2 . 2 − 3 x 2 x + 1
Chọn đáp án A
Đạo hàm của hàm số $y = (sin^23x)^\frac{\pi}{3}$ là:
A. $y' = sin6x . \pi . (sin^23x)^{\frac{\pi}{3}-1}$
B. $y' = 2sin3x . \pi . (sin^23x)^{\frac{\pi}{3}-1}$
C. $y' = 3cos6x . \pi . (sin^23x)^{\frac{\pi}{3}-1}$
D. $y' = cos2x . \pi . (sin^23x)^{\frac{\pi}{3}-1}$
Cho hàm số \(y=\sin2x+\cos2x+3.\) GTLN của hàm số trên\(\left[-\dfrac{\pi}{4};\dfrac{\pi}{4}\right]\) là số \(a+b\sqrt{2}.\) . Tính \(a+b\)
\(y=\sqrt{2}sin\left(2x+\dfrac{\pi}{4}\right)+3\)
Do \(sin\left(2x+\dfrac{\pi}{4}\right)\le1\Rightarrow y\le3+\sqrt{2}\)
\(\Rightarrow a=3;b=1\Rightarrow a+b=\)
Tính đạo hàm của hàm số y = x 3 x - 1 (Áp dụng căn bặc hai của u đạo hàm).
A. 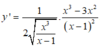
B. 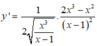
C. 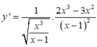
D. 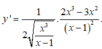
Tính đạo hàm của hàm số y = cos 2 x
A. y ' = sin 2 x 2 cos 2 x
B. y ' = - sin 2 x cos 2 x
C. y ' = sin 2 x cos 2 x
D. y ' = - sin 2 x 2 cos 2 x
Tính đạo hàm của hàm số y= căn cos(x²+2x+3)
Lời giải:
$y=\sqrt{\cos(x^2+2x+3)}$
$y'=\frac{-(x+1)\sin (x^2+2x+3)}{\sqrt{\cos (x^2+2x+3)}}$