Ta có : ĐK: m \(\ne\) 1 và -1
Tìm GTNN của P = \(\frac{3m^2-2m-1}{\left(m+1\right)^{ }^2}\)
Tìm GTNN của biểu thức sau:
\(A=\frac{3m^2-2m-1}{\left(m+1\right)^2}\)
Giải từng bước ra được ko @Nguyễn đình quý?
*Tìm hướng giải: Thông thường khi gặp bài này ta sẽ liên tưởng ngay tới \(\left(m+1\right)^2\ge0\) để từ đó tìm được x và thay vào tử tìm GTNN. Nhưng không được,vì để phân thức có nghĩa thì mẫu khác 0.Ta phải tìm hướng giải khác
*Hướng giải khác; Ta thử phân tích tử xem sao. ĐK \(m\ne-1\)
Ta có: \(3m^2-2m-1\)
\(=3\left(m^2-\frac{2}{3}m+\frac{1}{9}\right)-\frac{4}{3}\)
\(=3\left(m-\frac{1}{3}\right)^2-\frac{4}{3}\ge-\frac{4}{3}\)(do \(\left(m-\frac{1}{3}\right)^2\ge0\))
Thay vào A,ta có: \(A=\frac{3m^2-2m-1}{\left(m+1\right)^2}=\frac{3\left(m-\frac{1}{3}\right)^2-\frac{4}{3}}{\left(m+1\right)^2}\)
\(\ge\frac{\left(-\frac{4}{3}\right)}{\left(m+1\right)}=-\frac{4}{3\left(m+1\right)}=-\frac{4}{3m+3}\) (*)
Dấu "=" xảy ra khi \(m-\frac{1}{3}=0\Leftrightarrow m=\frac{1}{3}\)
Từ (*) suy ra \(\frac{1}{A}\ge-\frac{3m+3}{4}\ge-\frac{\frac{3.1}{3}+3}{4}=\frac{4}{4}=\frac{1}{1}\)
Suy ra \(A\ge\frac{1}{1}=1\)
Tìm GTNN của biểu thức sau:
\(A=\frac{3m^2-2m-1}{\left(m+1\right)^2}\)
\(A=\dfrac{3m^2-2m-1}{\left(m+1\right)^2}\)
\(=\dfrac{4m^2-\left(m^2+2m+1\right)}{m^2+2m+1}=\dfrac{4m^2}{\left(m+1\right)^2}-1\ge-1\)
Vậy \(Min_A=-1\Leftrightarrow m=0\)
 Bạn chịu khó nhìn hình nha! Mik lười bấm máy lắm!
Bạn chịu khó nhìn hình nha! Mik lười bấm máy lắm!
\(hpt:\hept{\begin{cases}3x+2y=-8\\-3x+\left(m+5\right)y=\left(m-1\right)\left(m+1\right)\end{cases}}\)
từ pt 1 \(\Rightarrow y=\frac{-8-3x}{2}\)(3)
thay (3) vào pt 2 ta được
\(-3mx+\left(m+5\right)\left(\frac{-8-3x}{2}\right)=\left(m-1\right)\left(m+1\right)\)
\(\Leftrightarrow-6mx-8m-40-15x-3mx=2\left(m^2-1\right)\)
\(\Leftrightarrow-9mx-15x=2m^2-2+40+8m\)
\(\Leftrightarrow x\left(-9m-15\right)=2m^2+8m+38\)(*)
để hệ phương trình có No duy nhất thì -9m-15\(\ne\)0 \(\Leftrightarrow m\ne\frac{-15}{9}\)
khi đó pt * có No: \(x=-\frac{2m^2+8m+38}{9m+15}\)
với \(x=-\frac{2m^2+8m+38}{9m+15}\)thì \(y=\left(-8+\frac{3\left(2m^2+8m+38\right)}{9m+15}\right):2=\frac{-8\left(9m+15\right)+3\left(2m^2+8m+38\right)}{9m+15}.\frac{1}{2}\)
\(=\frac{-72m-120+6m^2+24m+114}{9m+15}.\frac{1}{2}=\frac{6m^2-48m-6}{9m+15}.\frac{1}{2}=\frac{2\left(3m^2-24m-3\right)}{9m+15}.\frac{1}{2}=\frac{3m^2-24m-3}{9m+15}\)
M= \(x^2-\left(3m+1\right)x+2m^2+m-1\). tìm GTNN của M
B1: Cho pt \(x^2-2\left(m-1\right)x+2m-5=0\)(1)
a. Tìm m để (1) có 2 nghiệm dương
b. Gọi \(x_1,x_2\)là 2 nghiệm của (1). Tìm m để A=\(\left(\frac{x_1}{x_2}\right)^2+\left(\frac{x_2}{x_1}\right)^2\)nhận GT nguyên
B2: cho pt \(x^2-2\left(m-1\right)x+2m-3=0\)(1)
a. Tìm m để (1) có 2 nghiệm trái dấu
b. Tìm m để nghiệm này bằng bình phương nghiệm kia
B3: cho pt \(x^2-\left(3m+1\right)x+2m^2+m-1=0\)(1)
a. cmr pt (1) luôn có 2 nghiệm phân biệt \(\forall m\)
b. Tìm m để A=\(x_1^2+x_2^2-3x_1x_2\)đạt GTLN
B4: Cho pt \(x^2+\left(2m+3\right)x+3m+11=0\). Tìm m để pt có 2 nghiệm \(x_1,x_2\ne0\)thỏa mãn \(|\frac{1}{x_1}-\frac{1}{x_2}|=\frac{1}{2}\)
B5: cho 2 đường thẳng \(\left(d_1\right):y=\left(m-1\right)x-m^2-m\)và \(\left(d_2\right):y=\left(m-2\right)x-m^2-2m+1\)
a. Xđ tọa độ giao điểm của \(d_1\)và \(d_2\)(điểm G)
b. cmr điểm G thuộc 1 đường thẳng cố định khi m thay đổi
B6: cho pt \(2x^2-4mx+2m^2-1=0\)(1)
a. cmr pt (1) luôn có 2 nghiệm phân biệt \(\forall m\)
b. tìm m để pt (1) có 2 nghiệm thỏa mãn \(2x_1^2+4mx_2+2m^2-1>0\)
B7: cho pt \(x^2-2mx-16+5m^2=0\)(1)
a. tìm m để (1) có nghiệm
b. gọi \(x_1,x_2\)là 2 nghiệm của (1). Tìm GTLN và GTNN của biểu thức A=\(x_1\left(5x_1+3x_2-17\right)+x_2\left(5x_2+3x_1-17\right)\)
Cho hệ phương trình \(\left\{{}\begin{matrix}\left(2m+1\right)x+y=2m-2\\m^2x-y=m^2-3m\end{matrix}\right.\)
Trong đó \(m\in Z,m\ne-1\). Xác định m để hệ phương trình có nghiệm nguyên
\(\left\{{}\begin{matrix}\left(2m+1\right)x+y=2m-2\left(1\right)\\m^2x-y=m^2-3m\end{matrix}\right.\)
\(\Rightarrow\left(m^2+2m+1\right)x=m^2-m-2\)
\(\Rightarrow x=\dfrac{m^2-m-2}{m^2+2m+1}\left(m\ne-1\right)\)
\(\Rightarrow x=1+\dfrac{-3m-3}{m^2+2m+1}=1+\dfrac{-3\left(m+1\right)}{\left(m+1\right)^2}=1+\dfrac{-3}{m+1}\left(2\right)\)
\(\left(1\right)\left(2\right)\Rightarrow y=2m-2-\left(2m+1\right)\left(1-\dfrac{3}{m+1}\right)\)
\(\Rightarrow y=\dfrac{3m}{m+1}=3+\dfrac{-1}{m+1}\)
\(\Rightarrow x,y\in Z\left(m\in Z\right)\Leftrightarrow\left\{{}\begin{matrix}m+1\inƯ\left(3\right)=\left\{\pm1;\pm3\right\}\\m+1\inƯ\left(1\right)=\left\{\pm1\right\}\end{matrix}\right.\)
\(\Rightarrow m+1=\pm1\Leftrightarrow\left[{}\begin{matrix}m=0\left(tm\right)\\m=-2\left(tm\right)\end{matrix}\right.\)
Chứng minh rằng với mọi \(m\inℕ\), ta có :
a) \(\frac{4}{8m+5}=\frac{1}{2\left(m+1\right)}+\frac{1}{2\left(m+1\right)\left(3m+2\right)}+\frac{1}{2\left(3m+2\right)\left(8m+5\right)}\)
b) \(\frac{4}{3m+2}=\frac{1}{m+1}+\frac{1}{3m+2}+\frac{1}{\left(m+1\right)\left(3m+2\right)}\)
P/s : Giúp tớ câu này nha các cậu :33
a) Ta có:
\(\frac{1}{2\left(m+1\right)}+\frac{1}{2\left(m+1\right)\left(3m+2\right)}+\frac{1}{2\left(3m+2\right)\left(8m+5\right)}\)
\(=\frac{3m+2}{2\left(m+1\right)\left(3m+2\right)}+\frac{1}{2\left(m+1\right)\left(3m+2\right)}\)
\(+\frac{1}{2\left(3m+2\right)\left(8m+5\right)}\)
\(=\frac{3m+3}{2\left(m+1\right)\left(3m+2\right)}+\frac{1}{2\left(3m+2\right)\left(8m+5\right)}\)
\(=\frac{3\left(m+1\right)}{2\left(m+1\right)\left(3m+2\right)}+\frac{1}{2\left(3m+2\right)\left(8m+5\right)}\)
\(=\frac{3}{2\left(3m+2\right)}+\frac{1}{2\left(3m+2\right)\left(8m+5\right)}\)
\(=\frac{3\left(8m+5\right)}{2\left(3m+2\right)\left(8m+5\right)}+\frac{1}{2\left(3m+2\right)\left(8m+5\right)}\)
\(=\frac{24m+15}{2\left(3m+2\right)\left(8m+5\right)}+\frac{1}{2\left(3m+2\right)\left(8m+5\right)}\)
\(=\frac{24m+16}{2\left(3m+2\right)\left(8m+5\right)}\)
\(=\frac{8\left(3m+2\right)}{2\left(3m+2\right)\left(8m+5\right)}\)
\(=\frac{8}{2\left(8m+5\right)}=\frac{4}{8m+5}\left(đpcm\right)\)
b) Ta có: \(\frac{1}{m+1}+\frac{1}{3m+2}+\frac{1}{\left(m+1\right)\left(3m+2\right)}\)
\(=\frac{3m+2}{\left(m+1\right)\left(3m+2\right)}+\frac{m+1}{\left(m+1\right)\left(3m+2\right)}\)
\(+\frac{1}{\left(m+1\right)\left(3m+2\right)}\)
\(=\frac{4m+4}{\left(m+1\right)\left(3m+2\right)}\)
\(=\frac{4\left(m+1\right)}{\left(m+1\right)\left(3m+2\right)}\)
\(=\frac{4}{3m+2}\left(đpcm\right)\)
Tìm m để hai phương trình sau có nghiệm chung
a \(2x^2+\left(3m-1\right)x-3=0\) và \(6x^2-\left(2m-1\right)x-1=0\)
b \(x^2-mx+2m+1=0\) và \(mx^2-\left(2m+1\right)x-1=0\)
câu a
Gọi x0 là nghiệm chung của PT(1) và (2)
\(\Rightarrow\left\{{}\begin{matrix}2x^2_0+\left(3m-1\right)x_0-3=0\left(\times3\right)\\6.x^2_0-\left(2m-1\right)x_0-1=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}6x^2_0+3\left(3m-1\right)x_0-9=0\left(1\right)\\6x^2_0-\left(2m-1\right)x_0-1=0\left(2\right)\end{matrix}\right.\) Lấy (1)-(2) ,ta được
PT\(\Leftrightarrow3\left(3m-1\right)-9+\left(2m-1\right)+1\)=0
\(\Leftrightarrow9m-3-9+2m-1+1=0\Leftrightarrow11m-12=0\)
\(\Leftrightarrow m=\dfrac{12}{11}\)
Cho 2 đường thẳng
(d₁): y = \(\left(2+m\right)x+1\:\:\left(m\ne-2\right)\)
(d₂): y = \(\left(1+2m\right)x+2\:\left(m\ne-\dfrac{1}{2}\right)\)
a) Tìm m để (d₁) và (d₂) cắt nhau.
b) Với m = -1, vẽ (d₁) và (d₂) trên cùng một mặt phẳng tọa độ Oxy rồi tìm tọa độ giao điểm của 2 đường thẳng đó.
c) Tìm khoảng cách lớn nhất từ A(1;3) đến (d₁).
a: Để (d1) và (d2) cắt nhau thì \(2m+1\ne m+2\)
=>\(2m-m\ne2-1\)
=>\(m\ne1\)
b: Khi m=-1 thì (d1): \(y=\left(2-1\right)x+1=x+1\)
Khi m=-1 thì (d2): \(y=\left(1-2\right)x+2=-x+2\)
Vẽ đồ thị:
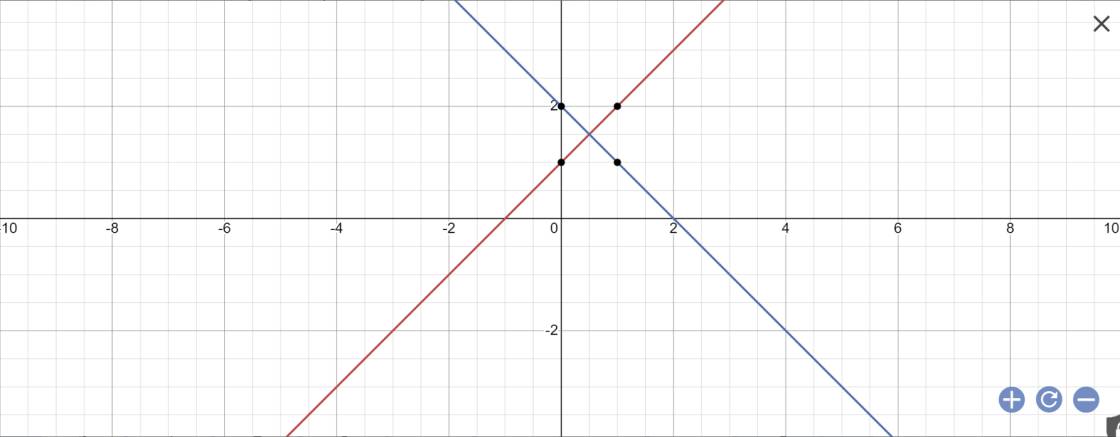
Phương trình hoành độ giao điểm là:
x+1=-x+2
=>x+x=2-1
=>2x=1
=>\(x=\dfrac{1}{2}\)
Thay x=1/2 vào y=x+1, ta được:
\(y=\dfrac{1}{2}+1=\dfrac{3}{2}\)
c:
(d1): y=(m+2)x+1
=>(m+2)x-y+1=0
Khoảng cách từ A(1;3) đến (d1) là:
\(d\left(A;\left(d1\right)\right)=\dfrac{\left|1\left(m+2\right)+3\cdot\left(-1\right)+1\right|}{\sqrt{\left(m+2\right)^2+\left(-1\right)^2}}\)
\(=\dfrac{\left|m\right|}{\sqrt{\left(m+2\right)^2+1}}\)
Để d(A;(d1)) lớn nhất thì m+2=0
=>m=-2
Vậy: \(d\left(A;\left(d1\right)\right)_{max}=\dfrac{\left|-2\right|}{\sqrt{\left(-2+2\right)^2+1}}=\dfrac{2}{1}=2\)