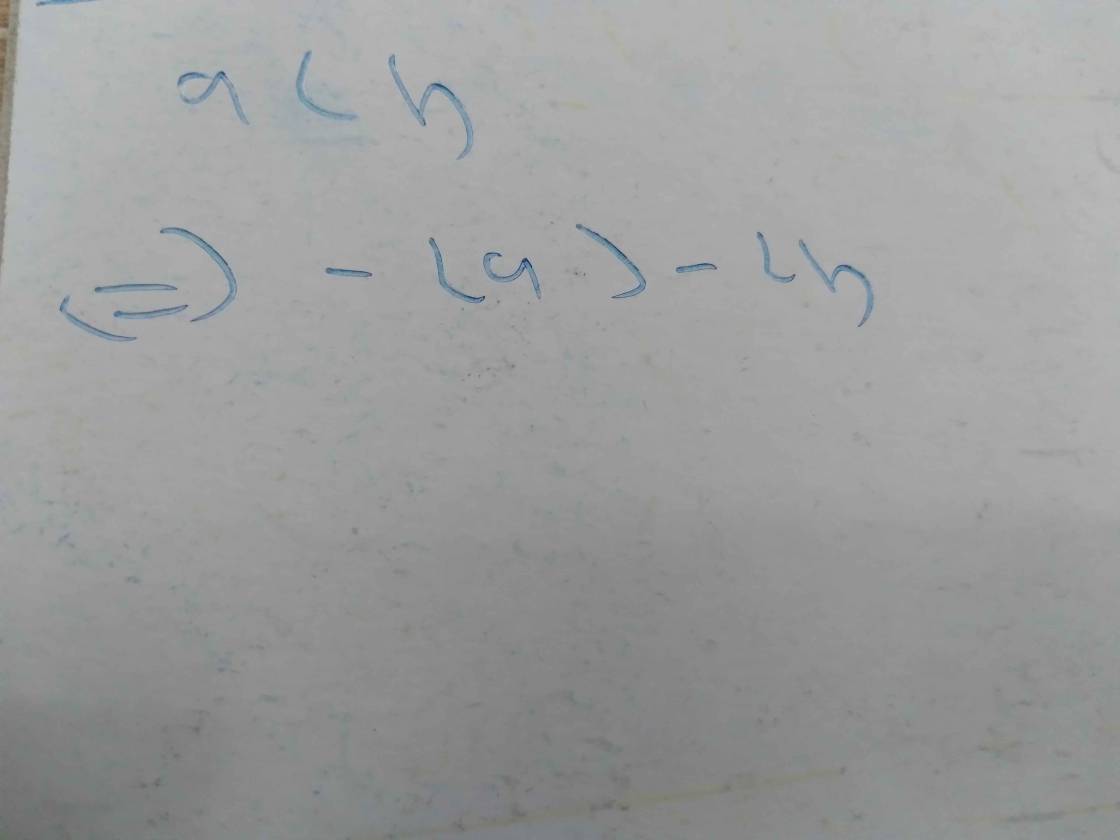Với \(A\in Z\), Hãy so sánh \(a^2\)và \(2a\)
Tuyển Cộng tác viên Hoc24 nhiệm kì 26 tại đây: https://forms.gle/dK3zGK3LHFrgvTkJ6
HL
Những câu hỏi liên quan
Với a \(\in\) Z. Hãy so sánh a2 và 2a.
Có đủ 3 trường hợp:
+) a2 = 2a khi a = 0 hoặc 2
Giải cụ thể:
a2 = 2a => a2 - 2a = 0
=> a(a-2) = 0 => a = 0;2
+) a2 > 2a khi a > 2 hoặc a < 0
+) a2 < 2a khi 0 < a < 2
Với a thuộc Z. Hãy so sánh a2 và 2a.
Làm nhanh hộ mình nhé.
bạn ơi gửi giúp mình đáp án đầy đủ nhé
Đúng 0
Bình luận (0)
ta co 2a=a+a,a mu 2=a.a.suy ra a mu 2 >2a (mk chi nghi vay thoi)
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
Với a thuộc z . hãy so sánh a2 với 2a
Có 3 trường hợp:
1) a2 > 2a (VD: 32 > 2.3)
2) a2 < 2a (VD:12 < 2.1)
3) a2 = 2a (VD:02 = 2.0)
Đúng 0
Bình luận (0)
với a thuộc z so sánh a^2 và 2a
TH1: a Là số âm ta có:
\(a^2\ge0\)với mọi a
\(2a< 0\)với mọi a
\(\Rightarrow a^2>2a\)
TH2: \(a=1\)
\(\Rightarrow a^2< 2a\left(1< 2\right)\)
TH3:\(a=0;a=2\)
\(\Rightarrow a^2=2a\left(4=4hoặc0=0\right)\)
TH4:\(a\ge3\)
\(\Rightarrow a^2>2a\)
VẬY:\(a^2>2a\)Khi \(a< 0;a\ge3\)
\(a^2=2a\)Khi \(a=0;a=2\)
\(a^2< 2a\)Khi \(a=1\)
Đúng 0
Bình luận (0)
Cho x=a/b; y= c/d; z= m/n
Trong đó m= (a+c)/2; n= (b+d)/2
a) Biết x khác y hãy so sánh x với z và y với z
b) Hãy so sánh y với t biết t= a+m/b+m và ad - bc= 1; cn - dm = 1
cho a<b hãy so sánh;
2a và 2b 2a và a+b -a và -b
\(a< b\)
\(\Leftrightarrow2a< 2b\)
\(a< b\)
\(\Leftrightarrow a+a< b+a\)
\(\Leftrightarrow2a< a+b\)
\(a< b\)
\(\Leftrightarrow-1a>-1b\)
\(\Leftrightarrow-a>-b\)
Đúng 0
Bình luận (0)
Do \(a< b\) , nên :
Gọi \(a=2,b=3\)
+ \(2a\Leftrightarrow2.2=4\)
\(2b=2.3=6\)
Mà \(4< 6\) \(\Rightarrow2a< 2b\)
+ \(2a\Leftrightarrow2.2=4\)
\(a+b\Leftrightarrow2+3=5\)
Mà \(4< 5\) \(\Rightarrow2a< a+b\)
+ \(-a\Leftrightarrow-1.2=-2\)
\(-b\Leftrightarrow-1.3=-3\)
Mà \(-2>-3\) \(\Rightarrow-a>-b\)
Đúng 1
Bình luận (0)
Cho a < b, hãy so sánh: 2a và 2b; 2a và a + b; -a + b; -a và -b.
+ a < b ⇒ 2a < 2b (nhân cả hai vế với 2 > 0, BĐT không đổi chiều).
+ a < b ⇒ a + a < b + a (Cộng cả hai vế với a)
hay 2a < a + b.
+ a < b ⇒ (-1).a > (-1).b (Nhân cả hai vế với -1 < 0, BĐT đổi chiều).
hay –a > -b.
Đúng 0
Bình luận (0)
Đề ôn tập HK 2 - Đề 8 Bài 1:a) Biết -3a - 1 -3b - 1. So sánh a và b?b) Biết 4a + 3 4b + 3. So sánh a và b?Bài 2: Biết a b, hãy so sánh:a) 3a - 7 và 3b - 7. b) 5 - 2a và 3 - 2bc) 2a + 3 và 2b + 3. d) 3a - 4 và 3b - 3Bài 3: a) Chứng minh pt: x² + 6x + 11 0 vô nghiệm b) Chứng minh bất pt: 5x² + 16 ≥ 0 có vô số nghiệm.
Đọc tiếp
Đề ôn tập HK 2 - Đề 8
Bài 1:
a) Biết -3a - 1 > -3b - 1. So sánh a và b?
b) Biết 4a + 3 < 4b + 3. So sánh a và b?
Bài 2: Biết a < b, hãy so sánh:
a) 3a - 7 và 3b - 7. b) 5 - 2a và 3 - 2b
c) 2a + 3 và 2b + 3. d) 3a - 4 và 3b - 3
Bài 3: a) Chứng minh pt: x² + 6x + 11 = 0 vô nghiệm
b) Chứng minh bất pt: 5x² + 16 ≥ 0 có vô số nghiệm.
1.
a. -3a - 1 + 1 > -3b - 1 + 1 (cộng cả 2 vế cho 1)
-3a . \(\left(\dfrac{-1}{3}\right)\) < -3b . \(\left(\dfrac{-1}{3}\right)\) (nhân cả vế cho \(\dfrac{-1}{3}\) )
a < b
b. 4a + 3 + (- 3) < 4b + 3 +(- 3) (cộng cả 2 vế cho -3)
4a . \(\dfrac{1}{4}\) < 4b . \(\dfrac{1}{4}\) (nhân cả 2 vế cho \(\dfrac{1}{4}\) )
a < b
2.
a. Ta có: a < b
3a < 3b ( nhân cả 2 vế cho 3)
3a - 7 < 3b - 7 (cộng cả 2 vế cho - 7 )
b. Ta có: a < b
-2a > -2b (nhân cả 2 vế cho -2)
5 - 2a > 5 - 2b ( cộng cẩ 2 vế cho 5)
c. Ta có: a < b
2a < 2b (nhân cả vế cho 2)
2a + 3 < 2b + 3 (cộng cả 2 vế cho 3)
d. Ta có: a < b
3a < 3b (nhân cả 2 vế cho 3)
3a - 4 < 3b - 4 (cộng cả 2 vế cho -4)
Ta có: 3 < 4
đến đây ko bắt cầu qua đc chắc đề bài sai
Đúng 1
Bình luận (0)
cho a<b , hãy so sánh-2a và -2b
Vì a<b
nên -2a > -2b ( nhân cả 2 vế với -2)
Đúng 0
Bình luận (0)
Có a<b nên -2a>-2b ( nhân cả 2 vế với -2 )
Đúng 0
Bình luận (0)