Cho góc xOy , điểm A nằm trong góc xOy và cách đều hai cạnh Ox ; Oy .
CM : OA là phân giác của góc xOy và hãy rút ra 1 nhận xét .
Cho góc xOy khác góc bẹt, điểm A thuộc cạnh Ox, điểm B thuộc cạnh Oy. Hãy tìm điểm M nằm trong góc xOy và cách đều hai cạnh Ox và Oy nên M thuộc tia phân giác Oz của ∠(xOy); cách đều Ox, Oy và cách đều A, B.
Vì điểm M nằm trong góc xOy và cách đều hai cạnh Ox và Oy nên M thuộc tia phân giác Oz của ∠(xOy).
Vì điểm M cách đều 2 điểm A và B nên M thuộc đường trung trực của AB.
Vậy M là giao điểm của đường trung trực của đoạn thẳng AB và tia phân giác Oz của ∠(xOy)
Do đó, có vô số điểm M thỏa mãn điều kiện trong câu a) khi OA = OB.
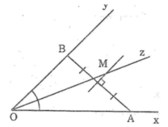
Cho góc xOy. Hai điểm A, B lần lượt nằm trên hai cạnh Ox, Oy.
Hãy tìm điểm M cách đều hai cạnh góc xOy và cách đều hai điểm A, B.
Tìm M khi độ dài đoạn OA, OB là bất kì
- Vì M cách đều hai cạnh Ox, Oy của góc xOy nên M nằm trên đường phân giác Oz của góc xOy (1).
- Vì M cách đều hai điểm A, B nên M nằm trên đường trung trực của đoạn AB (2).
Từ (1) và (2) ta xác định được điểm M là giao điểm của đường phân giác Oz của góc xOy và đường trung trực của đoạn AB.
Cho góc xOy. Hai điểm A, B lần lượt nằm trên hai cạnh Ox, Oy. Điểm M cách đều hai cạnh của góc xOy và cách đều hai điểm A, B. Xác định vị trí điểm M
A. Điểm M là giao điểm của tia phân giác góc (xOy) và đường trung trực của AB
B. Điểm M là giao điểm của tia phân giác góc (xOy) và AB
C. Điểm M là điểm bất kì thuộc tia phân giác của góc A
D. Điểm M là điểm thuộc đường trung trực của AB
Cho góc xOy. Hai điểm A, B lần lượt nằm trên hai cạnh Ox, Oy
a) Hãy tìm điểm M cách đều hai cạnh của góc xOy và cách đều hai điểm A, B
b) Nếu OA = OB thì có bao nhiêu điểm M thỏa mãn các điều kiện trong câu a ?
a) Tìm M khi độ OA, OB là bất kì
- Vì M cách đều hai cạnh Ox, Oy của góc xOy nên M nằm trên đường phân giác Oz của góc xOy (1).
- Vì M cách đều hai điểm A, B nên M nằm trên đường trung trực của đoạn AB (2).
Từ (1) và (2) ta xác định được điểm M là giao điểm của đường phân giác Oz của góc xOy và đường trung trực của đoạn AB.
b) Tìm M khi OA = OB
- Vì điểm M cách đều hai cạnh của góc xOy nên M nằm trên đường phân giác của góc xOy (3).
- Ta có OA = OB. Vậy ΔAOB cân tại O.
Trong tam giác cân OAB đường phân giác Oz cũng là đường trung trực của đoạn AB (4).
Từ (3) và (4) ta xác định được vô số điểm M nằm trên đường phân giác Oz của góc xOy thỏa mãn điều kiện bài toán.
a) Vì M cách đều hai cạnh Ox, Oy của ˆxOyxOy^ nên M phải thuộc tia phân giác ˆxOyxOy^.
Vì M cách đều hai điểm A và B nên M thuộc đường trung trực của AB. Vậy M là giao điểm của tia phân giác ˆxOyxOy^ và đường trung trực của đoạn thẳng AB.
b) Nếu OA = OB thì ∆AOB cân tại O nên tia phân giác ˆxOyxOy^ cũng là trung trực của AB nên mọi điểm trên tia phân giác ˆxOyxOy^ sẽ cách đều hai cạnh Ox, Oy và cách đều hai điểm A và B.
Vậy khi OA = OB thì mọi điểm trên tia phân giác ˆxOyxOy^ đều thỏa mãn các điều kiện ở câu a.
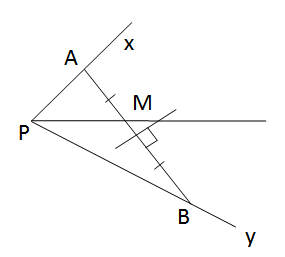
a) Vì M cách đều hai cạnh Ox, Oy của \(\widehat{xOy}\) nên M phải thuộc tia phân giác \(\widehat{xOy}\).
Vì M cách đều hai điểm A và B nên M thuộc đường trung trực của AB. Vậy M là giao điểm của tia phân giác \(\widehat{xOy}\) và đường trung trực của đoạn thẳng AB.
b) Nếu OA = OB thì ∆AOB cân tại O nên tia phân giác \(\widehat{xOy}\) cũng là trung trực của AB nên mọi điểm trên tia phân giác \(\widehat{xOy}\) sẽ cách đều hai cạnh Ox, Oy và cách đều hai điểm A và B.
Vậy khi OA = OB thì mọi điểm trên tia phân giác ˆxOyxOy^ đều thỏa mãn các điều kiện ở câu a.
Xem thêm tại: http://loigiaihay.com/bai-68-trang-88-sgk-toan-7-tap-2-c42a25479.html#ixzz4eh0oMuMO
Cho góc xOy khác góc bẹt, điểm A thuộc cạnh Ox, điểm B thuộc cạnh Oy
a) Hãy tìm điểm M nằm trong góc xOy, cách đều Ox, Oy và cách đều A, B
b) Nếu OA = OB thì có bao nhiêu điểm M thỏa mãn các điều kiện trong câu a) ?
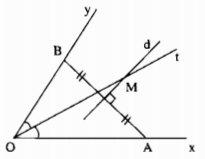
a) - Điểm nằm trong góc xOy và cách đều hai cạnh Ox và Oy nên nó thuộc tia phân giác Ot của góc xOy
- Điểm cách đều 2 điểm A và B thuộc đường thẳng d là đường trung trực của AB
Vậy M là giao điểm của dường trung trực của đoạn thẳng AB và tia phân giác Ot của góc xOy
b) Nếu OA = OB
⇒ ∆OAB cân tại O
Tia phân giác của góc xOy cũng là đường trung trực của AB. Vậy bất kỳ điểm M nào nằm trên tia phân giác của góc xOy đều thỏa mãn điều kiện câu a.
Cho góc nhọn xOy và điểm M nằm trong góc đó. Chứng minh rằng nếu M cách đều hai cạnh của góc xOy thì M nằm trên tia phân giác của góc này.
vẽ hình minh họa cho câu sau tập hợp các điểm nằm trong goc xOy và cách đều hai cạnh của góc đó là tia phân giác của góc xOy
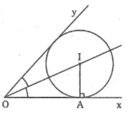
Cho góc xOy khác góc bẹt, điểm A nằm trên tia Ox. Dựng đường tròn (I) đi qua A và tiếp xúc với hai cạnh của góc xOy
* Phân tích
Giả sử đường tròn (I) dựng được thỏa mãn điều kiện bài toán
- Đường tròn (I) tiếp xúc với Ox và Oy nên điểm I nằm trên tia phân giác của góc xOy
- Đường tròn (I) tiếp xúc với Ox tại A nên I nằm trên đường vuông góc với Ox kẻ từ A
Vậy I là giao điểm của tia phân giác góc xOy và đường thẳng vuông góc với Ox tại A
* Cách dựng
- Dựng tia phân giác của góc xOy
- Dựng đường thẳng vuông góc với Ox tại A cắt tia phân giác của góc xOy tại I
- Dựng đường tròn (I; IA)
* Chứng minh
Ta có: Ox ⊥ IA tại A nên Ox là tiếp tuyến của (I)
I nằm trên tia phân giác của góc xOy nên I cách đều hai cạnh Ox, Oy. Khi đó khoảng cách từ I đến Oy bằng IA nên Oy cũng là tiếp tuyến của đường tròn (I).
Vậy đường tròn (I) đi qua A và tiếp xúc với hai cạnh của góc xOy.
* Biện luận
Vì góc xOy nhỏ hơn 180 ° nên góc tạo bởi một cạnh của góc với tia phân giác là góc nhọn. Khi đó đường thẳng vuông góc với Ox tại A luôn cắt tia phân giác của góc xOy.
Vẽ hình theo cách diễn đạt sau ( Mỗi ý là 1 hình ) :
1) Vẽ góc bẹt xOy.
2) Vẽ góc xOy, điểm A nằm trong góc xOy, điểm B nằm ngoài góc xOy.
3) Vẽ góc xOy, tia Oz nằm giữa hai tia Ox và Oy
4) Vẽ góc nCm và nCt sao cho tia Cm nằm giữa hai tia Cn và Ct
5) Vẽ các góc xOy; yOz; zOt và tOx sao cho góc xOz và yOt là các góc bẹt
6) Vẽ các góc xOy; yOz; zOt sao cho ia Oz nằm trong góc xOy; tia Oy nằm trong góc zOt và xOt là góc bẹt
7) Vẽ các góc xOy; yOz; zOt và tOx sao cho xOz là góc bẹt và hai tia Oy, Ot nằm trên hai nửa mặt phẳng đối nhau bờ xz