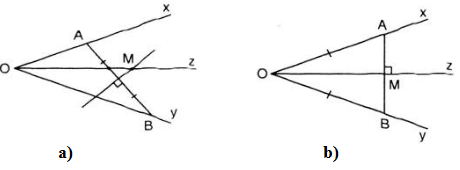
a) Tìm M khi độ OA, OB là bất kì
- Vì M cách đều hai cạnh Ox, Oy của góc xOy nên M nằm trên đường phân giác Oz của góc xOy (1).
- Vì M cách đều hai điểm A, B nên M nằm trên đường trung trực của đoạn AB (2).
Từ (1) và (2) ta xác định được điểm M là giao điểm của đường phân giác Oz của góc xOy và đường trung trực của đoạn AB.
b) Tìm M khi OA = OB
- Vì điểm M cách đều hai cạnh của góc xOy nên M nằm trên đường phân giác của góc xOy (3).
- Ta có OA = OB. Vậy ΔAOB cân tại O.
Trong tam giác cân OAB đường phân giác Oz cũng là đường trung trực của đoạn AB (4).
Từ (3) và (4) ta xác định được vô số điểm M nằm trên đường phân giác Oz của góc xOy thỏa mãn điều kiện bài toán.
a) Vì M cách đều hai cạnh Ox, Oy của ˆxOyxOy^ nên M phải thuộc tia phân giác ˆxOyxOy^.
Vì M cách đều hai điểm A và B nên M thuộc đường trung trực của AB. Vậy M là giao điểm của tia phân giác ˆxOyxOy^ và đường trung trực của đoạn thẳng AB.
b) Nếu OA = OB thì ∆AOB cân tại O nên tia phân giác ˆxOyxOy^ cũng là trung trực của AB nên mọi điểm trên tia phân giác ˆxOyxOy^ sẽ cách đều hai cạnh Ox, Oy và cách đều hai điểm A và B.
Vậy khi OA = OB thì mọi điểm trên tia phân giác ˆxOyxOy^ đều thỏa mãn các điều kiện ở câu a.
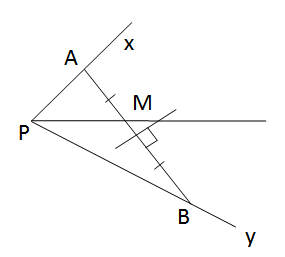
a) Vì M cách đều hai cạnh Ox, Oy của \(\widehat{xOy}\) nên M phải thuộc tia phân giác \(\widehat{xOy}\).
Vì M cách đều hai điểm A và B nên M thuộc đường trung trực của AB. Vậy M là giao điểm của tia phân giác \(\widehat{xOy}\) và đường trung trực của đoạn thẳng AB.
b) Nếu OA = OB thì ∆AOB cân tại O nên tia phân giác \(\widehat{xOy}\) cũng là trung trực của AB nên mọi điểm trên tia phân giác \(\widehat{xOy}\) sẽ cách đều hai cạnh Ox, Oy và cách đều hai điểm A và B.
Vậy khi OA = OB thì mọi điểm trên tia phân giác ˆxOyxOy^ đều thỏa mãn các điều kiện ở câu a.
Xem thêm tại: http://loigiaihay.com/bai-68-trang-88-sgk-toan-7-tap-2-c42a25479.html#ixzz4eh0oMuMO

a) Vì M cách đều hai cạnh Ox, Oy của ˆxOyxOy^ nên M phải thuộc tia phân giác ˆxOyxOy^.
Vì M cách đều hai điểm A và B nên M thuộc đường trung trực của AB. Vậy M là giao điểm của tia phân giác ˆxOyxOy^ và đường trung trực của đoạn thẳng AB.
b) Nếu OA = OB thì ∆AOB cân tại O nên tia phân giác ˆxOyxOy^ cũng là trung trực của AB nên mọi điểm trên tia phân giác ˆxOyxOy^ sẽ cách đều hai cạnh Ox, Oy và cách đều hai điểm A và B.
Vậy khi OA = OB thì mọi điểm trên tia phân giác ˆxOyxOy^ đều thỏa mãn các điều kiện ở câu a.
a) Tìm M khi độ OA, OB là bất kì
- Vì M cách đều hai cạnh Ox, Oy của góc xOy nên M nằm trên đường phân giác Oz của góc xOy (1).
- Vì M cách đều hai điểm A, B nên M nằm trên đường trung trực của đoạn AB (2).
Từ (1) và (2) ta xác định được điểm M là giao điểm của đường phân giác Oz của góc xOy và đường trung trực của đoạn AB.
b) Tìm M khi OA = OB
- Vì điểm M cách đều hai cạnh của góc xOy nên M nằm trên đường phân giác của góc xOy (3).
- Ta có OA = OB. Vậy ΔAOB cân tại O.
Trong tam giác cân OAB đường phân giác Oz cũng là đường trung trực của đoạn AB (4).
Từ (3) và (4) ta xác định được vô số điểm M nằm trên đường phân giác Oz của góc xOy thỏa mãn điều kiện bài toán.