Cho hệ phương trình x+ay=2 và
ax-2y=1
Tìm a để hpt có nghiệm thỏa mãn
x lớn hơn 0, y lớn hơn 0
Cho hệ phương trình: x+ay=2 và ax-27=1. Tìm các giá trị của a để hệ phương trình đã cho có nghiệm thỏa mãn điều kiện x>0, y<0.
Cho hệ phương trình { ax + 2y = 3
{ x - ay = 4
a) tìm a để có nghiệm thỏa mãn x>0; y>0
b) tìm a để có nghiệm thỏa mãn x và y là 2 số đối nhau.
Câu a): Xét \(a=0\) thấy hệ có nghiệm \(x=4,y=\frac{3}{2}\) thoả đề.
Xét \(a\ne0\). Nhân 2 vế pt dưới với \(a\): \(ax-a^2y=4a\).
Lúc này trừ 2 pt với nhau vế theo vế ta được: \(\left(a^2+2\right)y=3-4a\).
\(y=\frac{3-4a}{a^2+2}\) dương khi \(a\le\frac{3}{4}\).
\(x=ay+4=\frac{a\left(3-4a\right)+4\left(a^2+2\right)}{a^2+2}=\frac{3a+8}{a^2+2}\) dương khi \(a\ge-\frac{8}{3}\)
Vậy \(-\frac{8}{3}\le a\le\frac{3}{4}\). thoả câu a.
------
Câu b): Để hệ có nghiệm \(x=-y\) thì hệ sau phải có nghiệm: \(\hept{\begin{cases}ax-2x=3\\x+ax=4\end{cases}}\)
Trừ 2 pt vế theo vế được: \(3x=1\Leftrightarrow x=\frac{1}{3}\).
Thế vào tìm được \(a=11\)
Áp dụng định thức Grane :
\(D=-a^2-2\), \(D_x=-3a-8\), \(D_y=4a-3\)
Vì \(D=-a^2-2< 0\) nên hệ luôn có hai nghiệm phân biệt.
\(\hept{\begin{cases}x=\frac{D_x}{D}=\frac{3a+8}{a^2+2}\\y=\frac{D_y}{D}=\frac{3-4a}{a^2+2}\end{cases}}\). Theo đề thì \(\hept{\begin{cases}\frac{3a+8}{a^2+2}>0\\\frac{3-4a}{a^2+2}>0\end{cases}}\) \(\Leftrightarrow-\frac{8}{3}\le a\le\frac{3}{4}\)
b/ Ta có :\(x+y=0\) \(\Rightarrow\frac{3a+8}{a^2+2}+\frac{3-4a}{a^2+2}=0\) \(\Leftrightarrow\frac{-a+11}{a^2+2}=0\Leftrightarrow a=11\)
Cho hệ phương trình \(\hept{\begin{cases}x+ay=1\\-ax+y=a\end{cases}}\)
a, Tìm giá trị nguyên của a để hệ phương trình có nghiệm duy nhất (x;y) thỏa mãn 2x -y= a+1
b, tìm a để hệ có nghiệm (x;y) sao cho x<0; y<0
\(\hept{\begin{cases}x+ay=1\\\\-ax+y=a\end{cases}}\)
\(\Leftrightarrow\hept{\begin{cases}x=1-ay\\-a\left(1-ay\right)+y=a\end{cases}}\)
\(\Leftrightarrow\hept{\begin{cases}x=1-\frac{2a^2}{1+a^2}=\frac{1-a^2}{1+a^2}\\y=\frac{2a}{1+a^2}\end{cases}}\)
Theo đề bài ta có \(\hept{\begin{cases}x< 0\\y< 0\end{cases}}\)
\(\Leftrightarrow\hept{\begin{cases}1-a^2< 0\\2a< 0\end{cases}}\)
\(\Leftrightarrow x< -1\)
a/ Ta xem đây là hệ phương trình 3 ẩn rồi giải bình thường.
\(\hept{\begin{cases}x+ay=1\\-ax+y=a\\2x-y=a+1\end{cases}}\)
\(\Leftrightarrow\hept{\begin{cases}x=1-ay\\-a\left(1-ay\right)+y=a\\2\left(1-ay\right)-y=a+1\end{cases}}\)
Tới đây giải tiếp nhé. Không có bút giấy nháp nên giúp tới đây nhé. Chỉ cần thế là được nhé
Cho hệ phượng trình : \(\left\{\dfrac{x+y=2}{ax-2y=1}\right\}\)
a, giải hệ phượng trình với a = -1
b, tìm a để hệ phượng trình có nghiệm duy nhát thỏa mãn x >0 , y >0
a) Thay a=-1 vào hệ phương trình, ta được:
\(\left\{{}\begin{matrix}x+y=2\\-x-2y=1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}-y=1\\x+y=2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y=-1\\x-1=2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=3\\y=-1\end{matrix}\right.\)
Vậy: Khi a=-1 thì hệ phương trình có nghiệm duy nhất là (x,y)=(3;-1)
b) Ta có: \(\left\{{}\begin{matrix}x+y=2\\ax-2y=1\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}2x+2y=2\\ax-2y=1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}2x+ax=3\\x+y=2\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x\left(a+2\right)=3\\x+y=2\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x=\dfrac{3}{a+2}\\y=2-\dfrac{3}{a+2}=\dfrac{2a+4-3}{a+2}=\dfrac{2a+1}{a+2}\end{matrix}\right.\)
Vậy: Hệ phương trình có nghiệm duy nhất là \(\left(x,y\right)=\left(\dfrac{3}{a+2};\dfrac{2a+1}{a+2}\right)\)
Để x>0 và y>0 thì \(\left\{{}\begin{matrix}\dfrac{3}{a+2}>0\\\dfrac{2a+1}{a+2}>0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a+2>0\\2a+1>0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a>-2\\2a>-1\end{matrix}\right.\Leftrightarrow a>-\dfrac{1}{2}\)
Vậy: Để hệ phương trình có nghiệm duy nhất thỏa mãn x>0 và y>0 thì \(a>-\dfrac{1}{2}\)
Cho hệ phương trình :
x + a y = 3 a x - y = 2
b) Tìm điều kiện của a để hệ phương trình có nghiệm duy nhất thỏa mãn x + y > 0
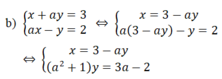
Do a 2 + 1 ≠ 0 ∀ x nên hệ phương trình trở thành:
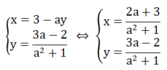
Khi đó:
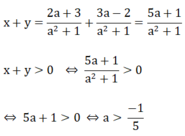
Vậy với a > (-1)/5 thì hệ phương trình có nghiệm duy nhất (x; y) thỏa mãn x+y >0
Cho \(\left\{{}\begin{matrix}x +my=2\\mx-2y=1\end{matrix}\right.\)a) tìm \(m\in Z\) để hệ có nghiệm duy nhất (x; y) sao cho x lớn hơn 0 và y lớn hơn 0 b) tìm \(m\in Z\) để hệ có nghiệm duy nhất (x; y) sao cho (x; y) nguyên
a) Ta có: \(\left\{{}\begin{matrix}x+my=2\\mx-2y=1\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}mx+m^2y=2m\\mx-2y=1\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}m^2y+2y=2m-1\\mx-2y=1\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}y\left(m^2+2\right)=2m-1\\mx=1+2y\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}y=\dfrac{2m-1}{m^2+2}\\x=\dfrac{1+2y}{m}=\left(1+\dfrac{2m-1}{m^2+2}\right)\cdot\dfrac{1}{m}\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x=\dfrac{m^2+2+2m-1}{m^2+2}\cdot\dfrac{1}{m}=\dfrac{m^2+2m+1}{m\left(m^2+2\right)}\\y=\dfrac{2m-1}{m^2+2}\end{matrix}\right.\)
Để hệ phương trình có nghiệm duy nhất thỏa mãn x>0 và y>0 thì \(\left\{{}\begin{matrix}\dfrac{m^2+2m+1}{m\left(m^2+2\right)}>0\\\dfrac{2m-1}{m^2+2}>0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}m>0\\2m-1>0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}m>0\\m>\dfrac{1}{2}\end{matrix}\right.\)
\(\Leftrightarrow m>\dfrac{1}{2}>0\)
Vậy: Khi m>0 thì hệ phương trình có nghiệm duy nhất (x,y) thỏa mãn x>0 và y>0
Cho hệ phương trình \(\left\{{}\begin{matrix}x+ay=3a\\-\text{ax}+y=2-a^2\end{matrix}\right.\)(*) với a là tham số. Tìm giá trị a để hệ phương trình (*) có nghiệm duy nhất (x,y) thỏa mãn \(\dfrac{2y}{x^2+3}\) là số nguyên
a, Tìm giá trị nguyên của m để nghiệm nguyên duy nhất (x;y) thỏa mãn 2x-y= m+ 1
b, Tìm a để hệ có nghiệm (x;y) sao cho x<0; y,0
lời giải có trước sau đó đổi đề cho phù hợp với lời giải