Áp dụng PTG: \(BC=\sqrt{AB^2+AC^2}=17\left(cm\right)\)

\(\cos\widehat{C}=\dfrac{AC}{BC}=\dfrac{15}{17};\tan\widehat{B}=\dfrac{AC}{AB}=\dfrac{15}{8}\)

a) Xét ΔABC vuông tại A và ΔHBA vuông tại H có 

\(\widehat{ABH}\) chung

Do đó: ΔABC\(\sim\)ΔHBA(g-g)

Câu a) với b) tính cos, tan, sin là tính góc hay cạnh vậy cậu?

a) Xét \(\Delta ABC\) vuông tại `A`

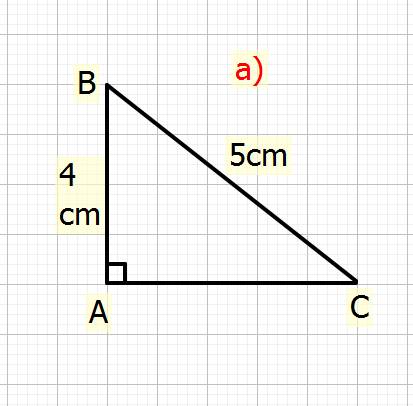
Ta có: \(BC^2=AB^2+AC^2\) (đl Pytago)

\(\Rightarrow5^2=4^2+AC^2\\ \Rightarrow AC^2=5^2-4^2\\ \Rightarrow AC^2=25-16=9\\ \Rightarrow AC=\sqrt{9}=3cm\) 

Vậy: \(AC=3cm\)

Ta có: \(CosC=\dfrac{AC}{BC}\left(tslg\right)\)

\(\Rightarrow CosC=\dfrac{3}{5}\\ \Rightarrow CosC\approx53^o\)

Vậy: Góc C khoảng \(53^o\)

Ta có: \(TanB=\dfrac{AC}{AB}\left(tslg\right)\)

\(\Rightarrow TanB=\dfrac{3}{4}\\ \Rightarrow TanB\approx37^o\)

Vậy: Góc B khoảng \(37^o\) 

_

b) Xét \(\Delta ABC\) vuông tại `A`

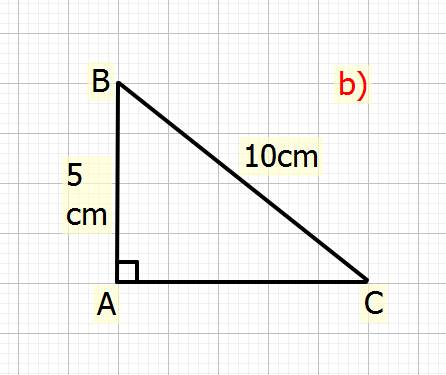
Ta có: \(BC^2=AB^2+AC^2\) (đl Pytago)

\(\Rightarrow10^2=5^2+AC^2\\ \Rightarrow AC^2=10^2-5^2\\\Rightarrow AC^2=100-25=75\\ \Rightarrow AC=\sqrt{75}=5\sqrt{3}cm\)

Vậy: \(AC=5\sqrt{3}cm\)

Ta có: \(SinC=\dfrac{AB}{BC}\left(tslg\right)\)

 \(\Rightarrow SinC=\dfrac{5}{10}\\ \Rightarrow30^o\)

Vậy: Góc C là \(30^o\)

Ta có: \(SinB=\dfrac{AC}{BC}\left(tslg\right)\)

\(\Rightarrow SinB=\dfrac{5\sqrt{3}}{10}\\ \Rightarrow SinB=60^o\)

Vậy: Góc B là \(60^o\).

AA lai Aa

\(a,cosC=\dfrac{5}{13}\\ Ta,có:cos^2C+sin^2C=1\\ \Rightarrow sinC=\sqrt{1-\left(\dfrac{5}{13}\right)^2}=\dfrac{12}{13}\\ cosB+sinC=1\\ \Leftrightarrow cosB+\dfrac{12}{13}=1\\ \Rightarrow cosB=\dfrac{1}{13}\\ tanC=\dfrac{sinC}{cosC}=\dfrac{\dfrac{12}{13}}{\dfrac{5}{13}}=\dfrac{12}{5}\)

\(b,tanB=\dfrac{1}{5}\Rightarrow\dfrac{sinB}{cosB}=\dfrac{1}{5}\Rightarrow cosB=5sinB\\ E=\dfrac{sinB-3cosB}{2sinB+3cosB}=\dfrac{sinB-3.5.sinB}{2sinB+3.5.sinB}=\dfrac{-14sinB}{17sinB}=-\dfrac{14}{17}\)