Giúp mik câu này với ạ!!
Tìm điều kiện của m để phương trình (m+7)x=2m-1 vô nghiệm.
Tuyển Cộng tác viên Hoc24 nhiệm kì 26 tại đây: https://forms.gle/dK3zGK3LHFrgvTkJ6
Giúp mình 2 câu này với ạ:
1. Tìm m để bất phương trình sau có nghiệm đúng với mọi x :
mx2 +(m+1)x+m-1 <0
2. Tìm m để bất phương trình sau vô nghiệm :
mx2-4(m+1)x+m-5<0
1.
\(\Leftrightarrow\left\{{}\begin{matrix}m< 0\\\Delta=\left(m+1\right)^2-4m\left(m-1\right)< 0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}m< 0\\-3m^2+7m+1< 0\end{matrix}\right.\)
\(\Leftrightarrow m< \dfrac{7-\sqrt{61}}{6}\)
2.
\(\Leftrightarrow\left\{{}\begin{matrix}m>0\\\Delta'=4\left(m+1\right)^2-m\left(m-5\right)\le0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}m>0\\3m^2+13m+4\le0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}m>0\\-4\le m\le-\dfrac{1}{3}\end{matrix}\right.\)
Không tồn tại m thỏa mãn
Tìm điều kiện của m để phương trình 2 m - 1 cos 2 x + 2 m . sin x . cos x = m - 1 vô nghiệm?
![]()
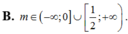
![]()
![]()
bài 1 Cho phương trình (m-1).x+m=0 (1)
a, Tìm điều kiện của m để phương trình (1) là phương trình bậc nhất một ẩn
b, tìm điều kiện của m để phương (1) có nghiệm x= -5
c, tìm điều kiện của m để phương trình (1) vô nghiêm
Giúp mình với tối mai đi học rồi
Câu 2 Cho phương trình 2x ^ 2 - 6x + 2m - 5 = 0 ( là tham số) a) Giải phương trình với m = 2 b) Tìm điều kiện của m để phương trình vô nghiệm? có nghiêm kịp? Có 2 nghiêm phân biệt?
a) 2x2 - 6x -1 = 0
delta phẩy = 9 + 2 = 11 = (\(\sqrt{11}\))2
x1 = \(\dfrac{3+\sqrt{11}}{2}\)
x2 = \(\dfrac{3-\sqrt{11}}{2}\)
b) xét delta phẩy có :
9 - 2.(2m-5) = 19 - 4m
+) điều kiện để phương trình vô nghiệm là 19 - 4m < 0 => m > \(\dfrac{19}{4}\)
+) điều kiện để phương trình có nghiệm kép là 19 - 4m = 0 => m = \(\dfrac{19}{4}\)
+) điều kiện để phương trình có 2 nghiệm phân biệt là 19 - 4m > 0
=> m < \(\dfrac{19}{4}\)
cho phương trình (m - 1.x+ m =0) a) Tìm điều kiện của m để phương trình trên là phương trình bậc nhất một ẩn. b)Tìm điều kiện của m để phương trình trên có nghiệm x = -5 c)Tìm điều kiện của m để phương trình trên vô nghiệm.
Ai giúp em bài này với ạ
Câu 1
A) |x-3| =5
B) |2x+3|=2|4-x|
C) |x^2-3x+1| =3-x
Câu 2 Tìm điều kiện của m để phương trình (X+3) (x^2-2x+m-1)=0 có ba nghiệm phân biệt
Câu 1:Ta có:
a) \(\left|x-3\right|=5\Leftrightarrow\left[{}\begin{matrix}x-3=5\\x-3=-5\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=8\\x=-2\end{matrix}\right.\)
b) \(\left|2x+3\right|=2.\left|4-x\right|\)
+)Xét \(\left\{{}\begin{matrix}2x+3\ge0\\4-x\ge0\end{matrix}\right.\) \(\Leftrightarrow\dfrac{-3}{2}\le x\le4\)
Khi đó \(2x+3=2\left(4-x\right)\Leftrightarrow2x+3=8-2x\Leftrightarrow4x=5\Leftrightarrow x=\dfrac{5}{4}\left(tm\right)\)
+) Xét \(\left\{{}\begin{matrix}2x+3\ge0\\4-x\le0\end{matrix}\right.\) \(\Leftrightarrow x\ge4\)
Khi đó: \(2x+3=2\left(x-4\right)=2x-8\Leftrightarrow0x=-11\left(vl\right)\)
+) Xét \(\left\{{}\begin{matrix}2x+3\le0\\4-x\ge0\end{matrix}\right.\) \(\Leftrightarrow x\le\dfrac{-3}{2}\)
Khi đó: \(-\left(2x+3\right)=2.\left(4-x\right)\Leftrightarrow-2x-3=8-2x\left(vl\right)\)
+)Xét \(\left\{{}\begin{matrix}2x+3\le0\\4-x\le0\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}x\le\dfrac{-3}{2}\\x\ge4\end{matrix}\right.\) \(\left(vl\right)\)
Vậy...
c) ĐKXĐ : \(3-x\ge0\Leftrightarrow x\le3\)
+)Xét \(x^{^2}-3x+1\ge0\)
\(\Leftrightarrow x^2-3x+1=3-x\Leftrightarrow x^2-2x-2=0\)
\(\Leftrightarrow x^2-2x+1=3\Leftrightarrow\left(x-1\right)^2=3\)
\(\Leftrightarrow\left[{}\begin{matrix}x-1=\sqrt{3}\\x-1=-\sqrt{3}\end{matrix}\right.\)\(\Leftrightarrow\left[{}\begin{matrix}x=1+\sqrt{3}\left(tm\right)\\x=1-\sqrt{3}\left(tm\right)\end{matrix}\right.\)
+)Xét \(x^{^2}-3x+1\le0\)
\(\Leftrightarrow-\left(x^2-3x+1\right)=3-x\)
\(\Leftrightarrow x^2-3x+1=x-3\Leftrightarrow x^2-4x+4=0\)
\(\Leftrightarrow\left(x-2\right)^2=0\Leftrightarrow x-2=0\Leftrightarrow x=2\left(tm\right)\)
Vậy...
Câu 2:
Ta có:
Phương trình \(\left(x+3\right)\left(x^2-2x+m-1\right)=0\) có một nghiệm là \(x=-3\)
\(\Rightarrow\)Phương trình \(\left(x+3\right)\left(x^2-2x+m-1\right)=0\) có ba nghiệm phân biệt khi và chỉ khi \(x^2-2x+m-1=0\) có 2 nghiệm phân biệt và khác \(-3\)
Ta có: \(x^2-2x+m-1=0\) có 2 nghiệm phân biệt khi và chỉ khi \(\text{△}>0\Leftrightarrow8-4m>0\Leftrightarrow m< 2\)
Gọi \(x_1\) và \(x_2\) là 2 nghiệm của phương trình \(x^2-2x+m-1=0\).Theo hệ thức Vi-ét ta có:
\(\left\{{}\begin{matrix}x_1+x_2=-\dfrac{-2}{1}=2\\x_1x_2=\dfrac{m-1}{1}=m-1\end{matrix}\right.\)\(\Leftrightarrow\left\{{}\begin{matrix}x_1=2-x_2\\\left(2-x_2\right).x_2=m-1\end{matrix}\right.\)
Nếu \(x_2\ne-3\) thì \(m-1\ne-15\Leftrightarrow m\ne-14\).
Do vai trò của \(x_1\) và \(x_2\) là như nhau nên \(x^2-2x+m-1=0\) có 2 nghiệm phân biệt và khác \(-3\) khi và chỉ khi: \(\left\{{}\begin{matrix}m< 2\\m\ne-14\end{matrix}\right.\)
Cho phương trình: x2 - 2(2m + 1)x + 4m2 + 4m = 0
Tìm các giá trị của m để phương trình (1) có hai nghiệm phân biệt x1, x2 thỏa mãn điều kiện:
| x1 - x2 | = x1 + x2
giải chi tiết ra giúp mình với ạ!
\(x^2-2\left(2m+1\right)x+4m^2+4m=0\)
Để pt có hai ng pb\(\Leftrightarrow\Delta>0\)
\(\Leftrightarrow4>0\left(lđ\right)\)
\(\Rightarrow\)Pt luôn có hai ng pb với mọi m
\(\left\{{}\begin{matrix}x_1=\dfrac{2\left(2m+1\right)+\sqrt{4}}{2}=2m+2\\x_2=\dfrac{2\left(2m+1\right)-\sqrt{4}}{2}=2m\end{matrix}\right.\)
Có \(\left|x_1-x_2\right|=x_1+x_2\)
\(\Leftrightarrow\left|2m+2-2m\right|=2m+2+2m\)
\(\Leftrightarrow2=4m+2\)
\(\Leftrightarrow m=0\)
Vậy...
Tham khảo
Tìm m để phương trình x2 – 2(2m + 1)x + 4m2 + 4m = 0
a)Cho phương trình : (m+2)x^2 - (2m-1)x-3+m=0 tìm điều kiện của m để phương trình có hai nghiệm phân biệt x1, x2 sao cho nghiệm này gấp đôi nghiệm kia
b)Cho phương trình bậc hai: x^2-mx+m-1=0. Tìm m để phương trình có hai nghiệm x1;x2 sao cho biểu thức R=2x1x2+3/x1^2+x2^2+2(1+x1x2) đạt giá trị lớn nhất. Tìm giá trị lớn nhất đó
c)Định m để hiệu hai nghiệm của phương trình sau đây bằng 2
mx^2-(m+3)x+2m+1=0
Mọi người giúp em giải chi tiết ra với ạ. Em cảm ơn!
Cho bất phương trình: (2m + 1)x + m - 5 ≥ 0
Tìm điều kiện của m để bất phương trình có nghiệm đúng với ∀x ∈ (0;1).
(2m + 1)x + m - 5 ≥ 0 ⇔ (2m + 1)x ≥ 5 - m (*)
TH1: 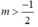 , bất phương trình (*) trở thành:
, bất phương trình (*) trở thành: 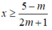
Tập nghiệm của bất phương trình là:
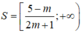
Để bất phương trình đã cho nghiệm đúng với ∀x ∈ (0;1)
thì (0;1) 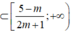
Hay 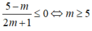
TH2: 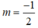 , bất phương trình (*) trở thành:
, bất phương trình (*) trở thành: 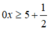
Bất phương trình vô nghiệm. ⇒ không có m .
TH3: Với 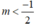 , bất phương trình (*) trở thành:
, bất phương trình (*) trở thành: 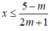
Tập nghiệm của bất phương trình là:
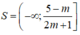
Để bất phương trình đã cho nghiệm đúng với ∀x ∈ (0;1)
thì (0;1) 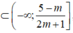
Hay 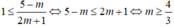
Kết hợp điều kiện 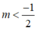 , ⇒ không có m thỏa mãn.
, ⇒ không có m thỏa mãn.
Vậy với m ≥ 5, bất phương trình đã cho nghiệm đúng với ∀x ∈ (0;1).