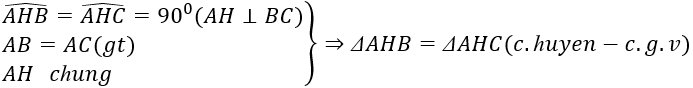| Bài 3 : Cho AABC cân tại A , kẻ AH vuông góc với BC ( HEBC ) . Biết AB = 15 cm ; AH = 12 cm . a ) Tính độ dài BH ? b ) Chứng minh HB = HC . c ) Kẻ HM vuông góc với AB , kẻ HN vuông góc với AC . Chứng minh : HM = HN . d ) Qua B , kẻ đường thẳng vuông với BC cắt tia CA tại D . Chứng minh rằng AABD cân .
H24
Những câu hỏi liên quan
Bài 15: Cho AABC có AB = 5 cm; AC = 12 cm ; BC = 13 cm a) Chứng minh AABC vuông tại A và tính độ dài đường cao AH;b) Kẻ HEl AB tại E, HF perp AC tại F. Chứng minh: AE.AB=AF.AC c) Chứng minh: A AEF và AABC đồng dạng.
bài 3: Cho tam giác ABC cân tại A có AB = AC = 5cm, BC = 8cm. Gọi H là trung điểm của BC. Tính AH
Bài 4: Cho ABC có AB= 15 cm, AC = 20 cm, BC = 25 cm. Kẻ AH vuông góc với BC tại H. a) Chứng minh: ABC vuông tại A b) Tính diện tích ABC c) Tính AH giúp mik với trình bày rõ cho mik nha
Bài 1: Cho tam giác cân tại A có BC=10 cm, AB=12 cm. Kẻ AH vuông góc với BC tại H. Tính độ dài AH?
Bài 2: Cho tam ABC vuông tại A có AC= 5 cm, AB=12 cm, M là trung điểm của BC. Qua M kẻ đường vuông góc với BC, cắt AB tại N. Biết MN= 2,7 cm. Tính độ dài BN?
Help me, please~ T^T
bài 1 : AH = \(\sqrt{119}\)cm
bài 2 : BN = \(\sqrt{49.54}\)cm
Đúng 0
Bình luận (0)
* hình tự vẽ
1/
Xét tam giác ABC: tam giác ABC là tam giác cân(gt) mà AH là đường cao(vì AH\(\perp\)BC)=> AH cũng là đường trung tuyến=> BH=HC
Ta có: BC=HB+HC, mà HB=HC(cmt)=> HB=HC=\(\frac{BC}{2}\)=> HB=HC= 5cm
Xét tam giác ACH, theo định lý Py ta go, có:
AH^2+ HC^2=AC^2
=> AH^2+ 5^2= 12^2
=> AH^2= 144-25
=> AH^2= 119=> AH= căn 119cm
2/ Xét tam giác BCA, theo định lý Py ta go, có:
BA^2+ AC^2= BC^2=> 12^2+5^2=BC^2
=> 144+25= BC^2=> BC^2= 169=>BC=13cm
Mà M là trung điểm BC(gt)=> MB=MC nên ta có BC=MB+MC=> MB=MC=\(\frac{BC}{2}\)=> MB=MC=6,5
Xét tam giác BMN, theo định lý Py ta go, có:
BN^2+NM^2= BM^2
=> BN^2+2,7^2=6,5^2=> BN^2 = 42,25-7,29=> BM^2= 34,96=> BM= căn 34,96cm
Đúng 1
Bình luận (0)
Bài 1 :
Xét \(\Delta ABC\)cân tại A \(\Rightarrow\hept{\begin{cases}AB=AC\\\widehat{B}=\widehat{C}\end{cases}}\)
Xét \(\Delta ABH\)và \(\Delta AHC\)có:
AB = AC (cmt)
\(\widehat{B}=\widehat{C}\)(cmt)
\(\widehat{AHB}=\widehat{AHC}\left(=90^o\right)\)
\(\Rightarrow\Delta ABH=\Delta ACH\left(Ch-gn\right)\)
\(\Rightarrow BH=HC\)( 2 cạnh tương ứng)
Mà BH + HC = BC
=> BH = HC = 1/2.BC = 5cm
Xét \(\Delta AHC\)
Áp dụng định lý Pytago có : AC2 = HC2 + AH2
=> 122=52+ AH2 => 144 = 25 + AH2 => AH2 = 144 - 25 = 119 => AH = \(\sqrt{119}\)(cm)
Vậy AH dài \(\sqrt{119}\)cm
Đúng 0
Bình luận (0)
Bài 4: Cho tam giác ABC vuông tại B có AB = 4cm, BC = 3cm. a/ Tính độ dài AC. b/ Từ B kẻ BH vuông góc với AC (H eAC). Chứng minh ABCH, AABC. c/ Từ H kẻ HI vuông góc với AB (I eAB). Tính IH biết AH=2 cm. d/ Gọi O là giao điểm của IC và BH. Tính diện tích tam giác IOB.
a: \(AC=\sqrt{4^2+3^2}=5\left(cm\right)\)
b: Xét ΔHBA vuông tại H và ΔHCB vuông tại H có
góc HBA=góc HCB
=>ΔHBA đồng dạng vơi ΔHCB
Đúng 0
Bình luận (0)
baiif 3: Cho tg ABC cân tại A có AB = AC = 5cm, BC = 8cm. Gọi H là trung điểm của BC. Tính AH
Bài 4: Cho ABC có AB= 15 cm, AC = 20 cm, BC = 25 cm. Kẻ AH vuông góc với BC tại H. a) Chứng minh: ABC vuông tại A b) Tính diện tích ABC c) Tính AH giải giúp mik với mik đag cần gấp cả cách trình bày và cách giải nhé
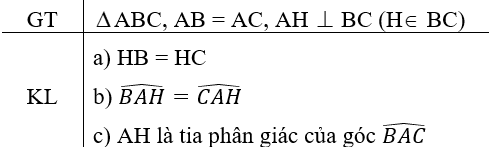
Bài 3: (5diểm) Cho tam giác ABC cân tại A, Kẻ AH vuông góc với BC(H € BC)
a) chứng minh ∆ABH=∆ACH
b) chứng minh AH là tia phân giác của góc BAC.
c) ChoAH = 3cm , BC - 8 cm . Tính độ dài AC.
d) Kẻ HE vuông góc với AB, HD vuông góc với AC . Chứng minh tam giác AED là tam giác cân.
a) Xét \(\Delta ABH\) vuông tại H và \(\Delta ACH\text{vuông tại H}:\)
AB = AC \((\Delta ABC\text{cân tại A}).\)
\(\widehat{B}=\widehat{C}\) \((\Delta ABC\text{cân tại A}).\)
\(\Rightarrow\Delta ABH=\Delta ACH\) (cạnh huyền - góc nhọn).
b) Xét \(\Delta ABC\) cân tại A:
AH là đường cao \(\left(AH\perp BC\right).\)
\(\Rightarrow\) AH là phân giác \(\widehat{BAC}.\)
c) Ta có: BH = CH = \(\dfrac{1}{2}BC=\dfrac{1}{2}8=4\left(cm\right).\)
Xét \(\Delta ABH:\)
\(AB^2=AH^2+BH^2\left(Pytago\right).\\ \Rightarrow AB^2=3^2+4^2.\\ \Rightarrow AB=5\left(cm\right).\)
Mà AB = AC (\(\Delta ABC\) cân tại A).
\(\Rightarrow AC=5\left(cm\right).\)
Đúng 1
Bình luận (0)
Mình đang cần gấp bài này. Mong các bạn giúp mình nhé. Cảm ơn các bạn
Bài 3: Cho tam giác ABC vuông tại A có AC=20cm. Kẻ AH vuông góc với BC. Biết BH=9cm,HC=16cm. Tính độ dài cạnh AB, AH?
Bài 6: Cho tam giác ABC cân tại A. Kẻ AH vuông góc với BC tại H. Cho BH=2cm,AB=4cm. Tính chu vi tam giác ABC.
Bài 3 :
\(BC=HC+HB=16+9=25\left(cm\right)\)
\(BC^2=AB^2+AC^2\Rightarrow AB^2=BC^2-AC^2=25^2-20^2=625-400=225=15^2\)
\(\Rightarrow AB=15\left(cm\right)\)
\(AH^2=HC.HB=16.9=4^2.3^2\Rightarrow AH=3.4=12\left(cm\right)\)
Bài 6:
\(AB=AC=4\left(cm\right)\) (Δ ABC cân tại A)
\(BH=HC=2\left(cm\right)\) (Ah là đường cao, đường trung tuyến cân Δ ABC)
\(BC=BH+HC=2+2=4\left(cm\right)\)
Chu vi Δ ABC :
\(4+4+4=12\left(cm\right)\)
Đúng 1
Bình luận (0)
Cho tam giác ABC cân tại A. Kẻ AH vuông góc BC (H thuộc BC).
a/ Chứng minh Tam giác AHB = Tam giác AHC. Từ đó suy ra HB = HC
b/ Biết AH = 8 cm, BC = 12 cm. Tính độ dài AC.
c/ Kẻ HD vuông góc với AB (D thuộc AB), kẻ HE vuông góc với AC (E thuộc AC). Chứng minh Tam giác HDE cân.
a: Xét ΔAHB vuông tại H và ΔAHC vuông tại H có
AB=AC
AH chung
=>ΔAHB=ΔAHC
=>HB=HC
b: BH=CH=12/2=6cm
=>AC=căn AH^2+HC^2=10cm
c: Xét ΔADH vuông tại D và ΔAEH vuông tại E có
AH chung
góc DAH=góc EAH
=>ΔADH=ΔAEH
=>HD=HE
=>ΔHDE cân tại H
Đúng 0
Bình luận (0)
Cho tam giác ABC cân tại A. Kẻ AH vuông góc BC (H thuộc BC).
a/ Chứng minh Tam giác AHB = Tam giác AHC. Từ đó suy ra HB = HC
b/ Biết AH = 8 cm, BC = 12 cm. Tính độ dài AC.
c/ Kẻ HD vuông góc với AB (D thuộc AB), kẻ HE vuông góc với AC (E thuộc AC). Chứng minh Tam giác HDE cân.
Chứng minh
a) Xét tam giác AHB và tam giác AHC có:
Đúng 1
Bình luận (0)
b) có tam giác ABC cân tại A
=> AB=AC
có BC=BH+HC
=> BC=12:2=6(cm)
=> BH=6;HC=6
có tam giác AHC
=> áp dụng định lí pytago có
=>AH2+HC2=AC2
=>82+62=AC2
=>AC2=102
=>AC=10
Đúng 1
Bình luận (0)