cho tam giác ABC cân .trên cạnh đáy BC lấy D sao cho CD=2BD.CMR:góc BAD<1/2 góc CAD
H24
Những câu hỏi liên quan
cho tam giác ABC cân .trên cạnh đáy BC lấy D sao cho CD=2BD.CMR:góc BAD<1/2 góc CAD
giúp mk nha
cho tam giác ABC cân. Trên cạnh đáy BC lấy điểm D sao cho: CD=2.BD. Chứng minh rằng:\(\widehat{BAD}=\frac{1}{2}\widehat{CAD}\)
Cho tam giác ABC cân. Trên cạnh đáy BC lấy điểm D sao cho CD=2BD. Chứng minh góc BAD= 1/2 góc CAD
MỌI NGƯỜI GIÚP EM!!! EM ĐANG GẤP!!! :) :) :)
Em tham khảo bài tương tự tại đây nhé.
Câu hỏi của Lê Tự Nhật Thạch - Toán lớp 7 - Học toán với OnlineMath
Đúng 0
Bình luận (0)
1. Cho tam giác ABC có AB > AC, tia phân giác của góc BAC cắt BC tại D. So sánh CD và BD.
2. Cho tam giác ABC cân tại A. Trên cạnh đáy BC lấy các điểm D, E sao cho BD = DE = EC. So sánh góc BAD và góc DAE.
Bài 1:
Xét ΔABC có AD là phân giác
nên BD/AB=CD/AC
mà AB>AC
nên BD>CD
Đúng 1
Bình luận (0)
Bài 3: Trên cạnh đáy BC của tam giác cân ABC lấy điểm D và E sao cho BD = DE = EC. Chứng minh rằng ∠BAD=∠EAC < ∠ DAE
Xét ΔADB và ΔAEC có
AB=AC
góc B=góc C
BD=CE
=>ΔADB=ΔAEC
=>góc BAD=góc CAE
Đúng 0
Bình luận (0)
Cho tam giác ABC cân. Trên cạnh đáy BC lấy điểm D sao cho CD = 2BD. So sánh số đo hai góc BAC và CAD
Em tham khảo bài tương tự tại đây nhé.
Câu hỏi của Lê Tự Nhật Thạch - Toán lớp 7 - Học toán với OnlineMath
Đúng 0
Bình luận (0)
Cho tam giác ABC cân.Yrên cạnh đáy BC lấy điểm D sao cho : CD=2.BD.CMR : góc BAD <1/2 góc CAD
cho tam giác ABC cân tại A. trên cạnh đáy BC lấy điểm D sao cho CD=2BD. chứng minh rằng góc B Â D < 1/2 C Â D.
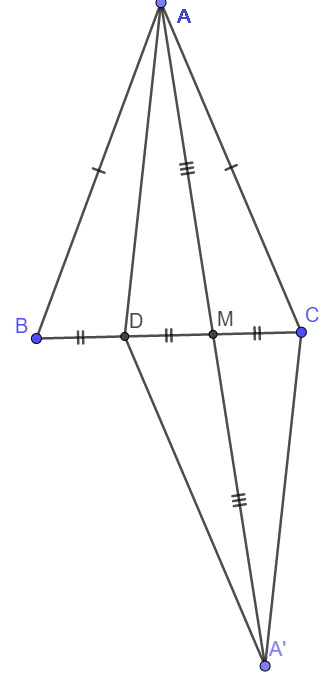
Gọi M là trung điểm DC và A' là điểm thuộc tia AM sao cho AM = MA'.
Khi đó ta thấy ngay \(\Delta AMC=\Delta A'MD\left(c-g-c\right)\)
\(\Rightarrow\widehat{MAC}=\widehat{MA'D}\) và AC = A'D.
Ta cũng có ngay \(\Delta ABD=\Delta ACM\left(c-g-c\right)\Rightarrow\widehat{BAD}=\widehat{CAM}\) và AB = AC
Kẻ AH vuông góc BC. Do tam giác ABC cân nên AH đồng thời là trung tuyến.
Vậy thì ta thấy ngay DH < BH nên theo quan hệ giữa đường xiên và hình chiếu ta có AD < AB
Suy ra AD < AC hay AD < DA'
Xét tam giác ADA' có AD < DA' nên theo quan hệ giữa cạnh và góc trong tam giác ta có :
\(\widehat{DAM}>\widehat{DA'M}\Rightarrow\widehat{DAM}>\widehat{MAC}\)
Lại có \(\widehat{DAM}+\widehat{MAC}=\widehat{CAD}\) nên \(\widehat{MAC}< \frac{1}{2}\widehat{CAD}\)
Vậy thì \(\widehat{BAD}< \frac{1}{2}\widehat{CAD}\left(đpcm\right)\)
Đúng 0
Bình luận (0)
cac yeu to nao de tam giac ABD=tam giac ACM z mi ban
Tam giác ABC cân tại A góc A=120 độ trên cạnh đáy BC lấy điểm D, E sao cho góc BAD=CAE=30 độ c/minh a, EC=EA b, tam giác ADE đều c, BD=DE=EC
ta có
\(\hept{\begin{cases}AB=AC\\\widehat{ABD}=\widehat{ACE}\\\widehat{BAD}=\widehat{CAE}\end{cases}\Rightarrow\Delta ABD=}\Delta ACE\left(c.g.c\right)\Rightarrow EC=EA\)
mà ta có \(\widehat{DAE}=\widehat{BAC}-\widehat{DAB}-\widehat{CAE}=120^0-30^0-30^0=60^0\)
do đó tam giác AEC cân và có một góc bằng 60 độ nên AEC đêu nên AE=EC=CA
mà ta có
\(\widehat{BAD}=\widehat{ABD}=30^0\Rightarrow BD=DA\) tương tự ta chúng minh được \(AE=EC\Rightarrow BD=DC=CE\)

