Bài 1 : Giải và biện luận theo tham số m phương trình : 3m -x =1-9m2x
Tuyển Cộng tác viên Hoc24 nhiệm kì 26 tại đây: https://forms.gle/dK3zGK3LHFrgvTkJ6
NL
Những câu hỏi liên quan
Bài 1: Giải và biện luận các phương trình sau theo tham số m a) 2mx + 3 = m - x b) m(x - 2) = 3x + 1
b: Để phương trình vô nghiệm thì x-2=0
hay x=2
Để phương trình có nghiệm thì x-2<>0
hay x<>2
Đúng 1
Bình luận (0)
giải và biện luận hệ phương trình sau theo tham số m :
\(\hept{\begin{cases}mx+y=3m-1\\x+my=m+1\end{cases}}\)
Giải và biện luận các phương trình sau theo tham số m: m2x + 6 = 4x + 3m
m2x + 6 = 4x + 3m
⇔ m2.x – 4x = 3m – 6
⇔ (m2 – 4).x = 3m – 6 (2)
+ Xét m2 – 4 ≠ 0 ⇔ m ≠ ±2, phương trình (2) có nghiệm duy nhất:
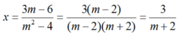
+ Xét m2 – 4 = 0 ⇔ m = ±2
● Với m = 2, pt (2) ⇔ 0x = 0 , phương trình có vô số nghiệm
● Với m = –2, pt (2) ⇔ 0x = –12, phương trình vô nghiệm.
Kết luận:
+ m = 2, phương trình có vô số nghiệm
+ m = –2, phương trình vô nghiệm
+ m ≠ ±2, phương trình có nghiệm duy nhất 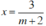
Đúng 0
Bình luận (0)
Giải và biện luận các phương trình sau theo tham số m.
2 x - 5 m = 2 x - 3 m

Kết luận:
Với m > 0 phương trình có nghiệm là x = 2m.
Với m = 0 phương trình có nghiệm là mọi số thực không âm.
Với m < 0 phương trình vô nghiệm.
Đúng 0
Bình luận (0)
Bài 1: Cho hệ phương trình với tham số m: hept{begin{cases}left(m-1right)x+y3m-4x+left(m-1right)ymend{cases}} a) Giải và biện luận hề phương trình. b) Tìm các giá trị của m để nghiệm của hệ phương trình là các số nguyên c) tìm các giá trị của m để hệ phương trình có nghiệm dương duy nhấtBài 2: Cho hệ phương trình với tham số m: hept{begin{cases}x+mym+1mx+y3m-1end{cases}} a) Giải và biện luận hệ phương trình theo m b) Trong trường hợp hệ có nghiệm duy nhất, tìm các giá trị của m để tích xy nhỏ...
Đọc tiếp
Bài 1: Cho hệ phương trình với tham số m:
\(\hept{\begin{cases}\left(m-1\right)x+y=3m-4\\x+\left(m-1\right)y=m\end{cases}}\)
a) Giải và biện luận hề phương trình.
b) Tìm các giá trị của m để nghiệm của hệ phương trình là các số nguyên
c) tìm các giá trị của m để hệ phương trình có nghiệm dương duy nhất
Bài 2: Cho hệ phương trình với tham số m:
\(\hept{\begin{cases}x+my=m+1\\mx+y=3m-1\end{cases}}\)
a) Giải và biện luận hệ phương trình theo m
b) Trong trường hợp hệ có nghiệm duy nhất, tìm các giá trị của m để tích xy nhỏ nhất.
Bài 1: Giải và biện luận các phương trình sau:
a) m(m-x)= 3(x+3)-6m
b) mx-3m=2x-3
c) (m^2 -9)x=m^2 +3m
Bài 2: Giải và biện luận các phương trình sau:
a) m(m-1)=2(2x+1)
b) (m^2 - 9)x=m^2 +3m
c) m(m-1)= 2(4-x)
d) (m^2 -3m+2)x= m-2
Các cậu giúp tớ với ạ, không cần làm hết đâu ạ, mng biết câu nào thì làm hộ tớ với nhé, plss!
Vì hai bài giống nhau nên anh sẽ làm mẫu bài 1 nhé.

Đúng 4
Bình luận (0)
Giải và biện luận bất phương trình sau theo tham số m.
( m - 1 ) . x ≤ 0
Điều kiện của bất phương trình là x ≥ 0
Nếu m ≤ 1 thì m - 1 ≤ 0, bất phương trình đã cho nghiệm đúng với mọi x ≥ 0
Nếu m > 1 thì m – 1 > 0, bất phương trình đã cho tương đương với √x ≤ 0 ⇔ x = 0
Vậy: Nếu m ≤ 1 thì tập nghiệm của bất phương trình là [0; +∞)
Nếu m > 1 thì tập nghiệm của bất phương trình là {0}
Đúng 0
Bình luận (0)
Giải và biện luận các phương trình sau theo tham số m: m(x - 2) = 3x + 1
m(x – 2) = 3x + 1
⇔ mx – 2m = 3x + 1
⇔ mx – 3x = 1 + 2m
⇔ (m – 3).x = 1 + 2m (1)
+ Xét m – 3 ≠ 0 ⇔ m ≠ 3, phương trình (1) có nghiệm duy nhất 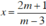
+ Xét m – 3 = 0 ⇔ m = 3, pt (1) ⇔ 0x = 7. Phương trình vô nghiệm.
Kết luận:
+ với m = 3, phương trình vô nghiệm
+ với m ≠ 3, phương trình có nghiệm duy nhất 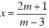
Đúng 0
Bình luận (0)
Bài 2: Giải và biện luận bất phương trình: \(m\left(x-m\right)\le4x+5\) theo tham số m
\(m\left(x-m\right)\le4x+5.\left(1\right)\\ \Leftrightarrow mx-m^2-4x-5\le0.\\ \Leftrightarrow\left(m-4\right)x\le5+m^2.\circledast\)
+) Nếu \(m-4>0.\Leftrightarrow m>4.\)
Khi \(\circledast\) có nghiệm: \(x\le\dfrac{5+m^2}{m-4}.\)
+) Nếu \(m-4< 0.\Leftrightarrow m< 4.\)
Khi \(\circledast\) có nghiệm: \(x\ge\dfrac{5+m^2}{m-4}.\)
+) Nếu \(m-4=0.\) \(\Leftrightarrow m=4.\)
Thay vào \(\circledast\) ta có:
\(0x\le5+4^2.\Leftrightarrow0x\le21\) (vô lý).
Kết luận:
Với \(m>4\) thì (1) có tập nghiệm \(S=\) \((-\infty;\dfrac{5+m^2}{m-4}].\)
Với \(m< 4\) thì (1) có tập nghiệm \(S=\) \([\dfrac{5+m^2}{m-4};+\infty).\)
Với \(m=4\) thì (1) có tập nghiệm \(S=\) \(\phi.\)
Đúng 0
Bình luận (0)
Giải và biện luận theo tham số m nghiệm của phương trình: \(\dfrac{\left(m-1\right)x+2}{x-2}=m+1\)
Xem chi tiết
Phương trình tương đương
\(\left\{{}\begin{matrix}\left(m-1\right)x+2=\left(m+1\right)\left(x-2\right)\\x\ne2\end{matrix}\right.\)
⇔ \(\left\{{}\begin{matrix}\left(m-1\right)x+2=\left(m+1\right)x-2m-2\\x\ne2\end{matrix}\right.\)
⇔ \(\left\{{}\begin{matrix}\left(m-1-m-1\right)x=-2m-4\\x\ne2\end{matrix}\right.\)
⇔ \(\left\{{}\begin{matrix}-2x=-2m-4\\x\ne2\end{matrix}\right.\)
⇔ \(\left\{{}\begin{matrix}x=m+2\\x\ne2\end{matrix}\right.\)
Nếu m = 0 thì phương trình vô nghiệm
Nếu m ≠ 0 thì S = {m + 2}
Đúng 3
Bình luận (0)




