Tìm tọa độ giao điểm của đường thẳng y=x+3 và (P) y=-x2+3x+2
H24
Những câu hỏi liên quan
Tìm tọa độ giao điểm của (P) y = 1/2 x 2 và đường thẳng (d) y=(-1)/2 x+3
Hoành độ giao điểm của (P) và (d) là nghiệm của phương trình
1/2 x 2 = (-1)/2 x + 3 ⇔ x 2 + x - 6 = 0
Δ = 1 - 4.1.(-6) = 25 > 0
⇒ Phương trình có 2 nghiệm phân biệt
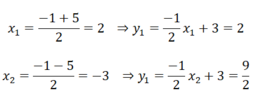
Vậy tọa độ giao điểm của (P) và (d) là (2; 2) và (-3; 9/2)
Đúng 0
Bình luận (0)
a.Cho parabol (P): y = x2 và đường thẳng (d): y = 3x - 2
Hãy tìm tọa độ giao điểm của đường thẳng (d) và parabol(P) bằng phương pháp đại số.
b.Cho phương trình x2 - 2(m + 1)x + 2m - 3 = 0
với m là tham số.Chứng minh rằng phương trình luôn có hai nghiệm phân biệt với mọi giá trị của m.
a: PTHĐGĐ là:
x^2-3x+2=0
=>(x-2)(x-1)=0
=>x=2 hoặc x=1
Khi x=2 thì y=2^2=4
Khi x=1 thì y=1^2=1
b: Δ=(2m+2)^2-4(2m-3)
=4m^2+8m+4-8m+12
=4m^2+16>0
=>Phương trình luôn có hai nghiệm
Đúng 0
Bình luận (0)
Câu 1 Giải pt sau
a) x2-2x-3=0
b)-x2+7x-6=0
Câu 2 a) vẽ biểu đồ hàm số y=x2(P)
B)Tìm tọa độ giao điểm của đường thẳng y=3x-2 và parabol (p)
Xem chi tiết
a) x2 - 2x - 3 = 0
Dễ thấy pt có a - b + c = 0 nên có hai nghiệm x1 = -1 ; x2 = 3
Vậy phương trình có hai nghiệm x1 = -1 ; x2 = 3
b) -x2 + 7x - 6 = 0
Dễ thấy pt có a + b + c = 0 nên có hai nghiệm x1 = 1 ; x2 = 6
Vậy phương trình có hai nghiệm x1 = 1 ; x2 = 6
*đths e chưa làm đc vì mới lớp 8 :v*
Cho parabol (P): y = x2 và đường thẳng (d): y = 3x - 2
Hãy tìm tọa độ giao điểm của đường thẳng (d) và parabol(P) bằng phương pháp đại số.
Hoành độ giao điểm tm pt
\(x^2-3x+2=0\Leftrightarrow x=1;x=2\)
\(\Rightarrow y=1;y=4\)
Vậy (P) cắt (d) tại A(1;1) ; B(2;4)
Đúng 2
Bình luận (0)
1. Tìm tọa độ giao điểm 2 đường thẳng: y = 3x + 2 và y = 2x - 3
2. Tìm m để 3 đường thẳng y = 3x + 2 ; y = 2x - 3; y = (m - 2)x + 3 - m đồng quy
1) Tọa độ giao điểm của 2 đường thẳng y=3x+2 và y=2x-3 là nghiệm của hệ phương trình:
\(\left\{{}\begin{matrix}y=3x+2\\y=2x-3\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}3x+2=2x-3\\y=3x+2\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}3x+2-2x+3=0\\y=3x+2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x+5=0\\y=3x+2\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x=-5\\y=3\cdot\left(-5\right)+2=-15+2=-13\end{matrix}\right.\)
Vậy: Tọa độ giao điểm của 2 đường thẳng y=3x+2 và y=2x-3 là (-5;-13)
2) Đặt (d1): y=3x+2;
(d2): y=2x-3;
(d3): y=(m-2)x+3-m
Tọa độ giao điểm của (d1) và (d2) là nghiệm của hệ phương trình:
\(\left\{{}\begin{matrix}y=3x+2\\y=2x-3\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}3x+2=2x-3\\y=2x-3\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x=-5\\y=2\cdot\left(-5\right)-3=-13\end{matrix}\right.\)
Để (d1), (d2) và (d3) đồng quy thì (d3) đi qua tọa độ giao điểm của (d1) và (d2)
Thay x=-5 và y=-13 vào (d3), ta được:
\(\left(m-2\right)\cdot\left(-5\right)+3-m=-13\)
\(\Leftrightarrow-5m+10+3-m+13=0\)
\(\Leftrightarrow-6m+26=0\)
\(\Leftrightarrow-6m=-26\)
hay \(m=\dfrac{13}{3}\)
Vậy: Để 3 đường thẳng y=3x+2; y=2x-3 và y=(m-2)x+3-m đồng quy thì \(m=\dfrac{13}{3}\)
Đúng 1
Bình luận (0)
hãy vẽ parabol (p) và đường thẳng (d) trên cùng mặt phẳng tọa độ. Tìm tọa độ giao điểm của chúng bằng phép tính: (p) :y =x2 và (d) :y =x-3
Tìm tọa độ giao điểm của 2 đường thẳng y= 2x -3 và y=3x+1
ptr hoành độ giao điểm:
2x2= 3x-1
=> 2x2 - 3x+1 =0
=> (x-1)(2x-1) = 0
=> x=1; y= 2 hoặc x =1/2; y=1/2
Đúng 3
Bình luận (0)
y = - 3x + 2 y = 1/3 x - 3 a)Gọi giao điểm của đường thẳng y = - 3x + 2 ; y = - 3x - x + 3 với trục hoành theo thứ tự A,B và giao điểm là C b)Tìm tọa đó A, B ,C c)Tính độ dài AB, AC, BC
b: y=-3x-x+3=-4x+3
Tọa độ A là:
\(\left\{{}\begin{matrix}y=0\\-3x+2=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y=0\\3x=2\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}y=0\\x=\dfrac{2}{3}\end{matrix}\right.\)
Tọa độ B là:
\(\left\{{}\begin{matrix}y=0\\-4x+3=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y=0\\-4x=-3\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x=\dfrac{3}{4}\\y=0\end{matrix}\right.\)
Tọa độ C là:
\(\left\{{}\begin{matrix}-3x+2=-4x+3\\y=-3x+2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}-3x+4x=3-2\\y=-3x+2\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x=1\\y=-3\cdot1+2=-3+2=-1\end{matrix}\right.\)
Vậy: \(A\left(\dfrac{2}{3};0\right);B\left(\dfrac{3}{4};0\right);C\left(1;-1\right)\)
c: \(AB=\sqrt{\left(\dfrac{3}{4}-\dfrac{2}{3}\right)^2+\left(0-0\right)^2}\)
\(=\sqrt{\left(\dfrac{9-8}{12}\right)^2}=\dfrac{1}{12}\)
\(AC=\sqrt{\left(1-\dfrac{2}{3}\right)^2+\left(-1-0\right)^2}=\sqrt{\left(\dfrac{1}{3}\right)^2+1^2}=\sqrt{1+\dfrac{1}{9}}=\sqrt{\dfrac{10}{9}}=\dfrac{\sqrt{10}}{3}\)
\(BC=\sqrt{\left(1-\dfrac{3}{4}\right)^2+\left(-1-0\right)^2}\)
\(=\sqrt{\left(\dfrac{1}{4}\right)^2+\left(-1\right)^2}\)
\(=\sqrt{\dfrac{1}{16}+1}=\sqrt{\dfrac{17}{16}}=\dfrac{\sqrt{17}}{4}\)
Đúng 2
Bình luận (0)
Trong mặt phẳng tọa độ Oxy, cho Parabol (P):
y = x2 và đường thẳng (d): y = -x + 2
a) Tìm tọa độ giao điểm của (P) và (Q)
b) Gọi A, B là hai giao điểm của (P) và (Q). Tính diện tích tam giác OAB.
\(\left\{{}\begin{matrix}\left(P\right):y=x^2\\\left(d\right):y=-x+2\end{matrix}\right.\)
a) Tọa độ giao điểm của (P) và (Q) là nghiệm của hệ phương trình
\(\left\{{}\begin{matrix}y=x^2\\y=-x+2\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}y=x^2\\x^2=-x+2\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}y=x^2\\x^2+x-2=0\left(1\right)\end{matrix}\right.\)
\(pt\left(1\right)\Leftrightarrow\left[{}\begin{matrix}x=1\\x=-2\end{matrix}\right.\) \(\left(a+b+c=1+1-2=0\right)\)
\(hpt\Leftrightarrow\left[{}\begin{matrix}\left\{{}\begin{matrix}x=1\\y=1\end{matrix}\right.\\\left\{{}\begin{matrix}x=-2\\y=4\end{matrix}\right.\end{matrix}\right.\)
Vậy tọa độ giao điểm của (P) và (Q) là \(A\left(1;1\right)\&B\left(-2;4\right)\)
Đúng 1
Bình luận (0)
a) Phương trình hoành độ giao điểm :
x2 = - x + 2
<=> (x - 1)(x + 2) = 0
<=> \(\left[{}\begin{matrix}x=1\\x=-2\end{matrix}\right.\)
Với x = 1 ta được y = 1
Với x = -2 ta được y = 4
Vậy tọa độ giao điểm là A(1; 1) ; B(-2;4)
b) Gọi C(-2 ; 0) ; D(1;0)
ta được \(S_{AOB}=S_{ABCD}-S_{BOC}-S_{AOD}\)
\(=\dfrac{\left(BC+AD\right).CD}{2}-\dfrac{BC.CO}{2}-\dfrac{AD.DO}{2}\)
\(=\dfrac{\left(4+1\right).3}{2}+\dfrac{4.2}{2}+\dfrac{1.1}{2}=12\) (đvdt)
Đúng 1
Bình luận (0)
Vẽ đồ thị các hàm số sau trên cùng 1 mặt phẳng tọa độ và tìm tọa độ giao điểm của 2 đường thẳng đó:
a) y = 2x và y = -3x + 5
b) y = 3x + 2 và y = \(-\dfrac{1}{2}x+1\)
c) y = \(\dfrac{3}{2}x-2\) và y = \(-\dfrac{1}{2}x\:+2\)
d) y = -2x + 5 và y = x + 2
Bạn tự vẽ nhé.
\(a,\) 2 đồ thị hàm số \(y=2x,y=-3x+5\) giao nhau khi và chỉ khi :
\(2x=-3x+5\\ \Leftrightarrow5x=5\\ \Leftrightarrow x=1\)
Thay \(x=1\) vào \(y=2x\Leftrightarrow y=2\)
Vậy giao điểm của 2 đồ thị là \(\left(1;2\right)\)
\(b,\) 2 đồ thị hàm số \(y=3x+2,y=-\dfrac{1}{2}x+1\) giao nhau khi và chỉ khi :
\(3x+2=-\dfrac{1}{2}x+1\\ \Leftrightarrow\dfrac{7}{2}x=-1\\ \Leftrightarrow x=-\dfrac{2}{7}\)
Thay \(x=-\dfrac{2}{7}\) vào \(y=3x+2\Rightarrow y=\dfrac{8}{7}\)
Vậy giao điểm của 2 đồ thị là \(\left(-\dfrac{2}{7};\dfrac{8}{7}\right)\)
\(c,\) 2 đồ thị hàm số \(y=\dfrac{3}{2}x-2,y=-\dfrac{1}{2}x+2\) giao nhau khi và chỉ khi :
\(\dfrac{3}{2}x-2=-\dfrac{1}{2}x+2\\ \Leftrightarrow2x=4\\ \Leftrightarrow x=2\)
Thay \(x=2\) vào \(y=\dfrac{3}{2}x-2\Rightarrow y=1\)
Vậy giao điểm của 2 đồ thị là \(\left(2;1\right)\)
\(d,\) 2 đồ thị hàm số \(y=-2x+5,y=x+2\) giao nhau khi và chỉ khi :
\(-2x+5=x+2\\ \Leftrightarrow-3x=-3\\ \Leftrightarrow x=1\)
Thay \(x=1\) vào \(y=x+2\Rightarrow y=3\)
Vậy giao điểm của 2 đồ thị là \(\left(1;3\right)\)
Đúng 1
Bình luận (0)









