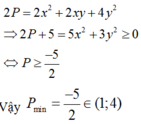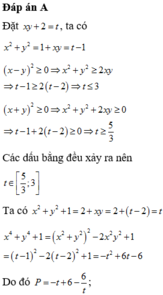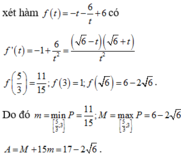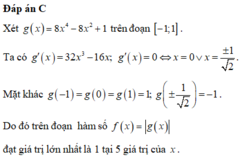cho hai số thực x, y thay đổi nhưng luôn thỏa mãn x+y = 4. tìm giá trị nhỏ nhất A= x4+y4
TP
Những câu hỏi liên quan
Cho biểu thức P=x2+y2 với x,y là hai số thực thay đổi nhưng luôn thỏa mãn x+y+xy=15. tìm giá trị nhỏ nhất của biểu thức P
Ta có: \(15=x+y+xy\le x+y+\frac{\left(x+y\right)^2}{4}\Rightarrow\frac{t^2}{4}+t\ge15\)(\(t=x+y\))
\(\Leftrightarrow\left(t-6\right)\left(t+10\right)\ge0\Leftrightarrow\orbr{\begin{cases}t\ge6\\t\le-10\end{cases}}\)
\(P=x^2+y^2=\frac{1}{2}.2\left(x^2+y^2\right)\ge\frac{1}{2}\left(x+y\right)^2\ge\frac{1}{2}.6^2=18\)
Dấu \(=\)xảy ra khi \(x=y=3\).
Cho các số thực x,y thay đổi nhưng luôn thỏa mãn
3
x
2
-
2
x
y
-
y
2
5
. Giá trị nhỏ nhất của biểu thức
P
:
x
2
+
x
y
+
2
y
2
thuộc khoảng nào sau đây? A. (4;7) B. ...
Đọc tiếp
Cho các số thực x,y thay đổi nhưng luôn thỏa mãn 3 x 2 - 2 x y - y 2 = 5 . Giá trị nhỏ nhất của biểu thức P : x 2 + x y + 2 y 2 thuộc khoảng nào sau đây?
A. (4;7)
B. - 2 ; 1
C. 1 ; 4
D. 7 ; 10
Cho x, y là những số thực thỏa mãn
x
2
–
x
y
+
y
2
1
. Gọi M và m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của
P
x
4
+
y
4
+
1
x...
Đọc tiếp
Cho x, y là những số thực thỏa mãn x 2 – x y + y 2 = 1 . Gọi M và m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của P = x 4 + y 4 + 1 x 2 + y 2 + 1 . Giá trị của A = M + 15 m là
A. A = 17 - 2 6
B. A = 17 - 6
C. A = 17 + 6
D. A = 17 + 2 6
Cho x,y là những số thực thỏa mãn
x
2
-
x
y
+
y
2
1
. Gọi M và m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của
P
x
4
+
y
4
+
1
x
2
+
y...
Đọc tiếp
Cho x,y là những số thực thỏa mãn x 2 - x y + y 2 = 1 . Gọi M và m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của P = x 4 + y 4 + 1 x 2 + y 2 + 1 . Giá trị của A = M + 15m là
A. A = 17 - 2 6
B. A = 17 + 6
C. A = 17 + 2 6
D. A = 17 - 6
cho hai số x,y thỏa mãn x2 + y2 =1 + xy , gọi M và m lần lượt là giá trị lớn nhất , giá trị nhỏ nhất của P = x4 + y4 -x2y2 , tính tích Mm
\(x^2+y^2=1+xy\Rightarrow x^2+y^2-xy=1\)
Ta có: \(1+xy=x^2+y^2\ge2xy\Rightarrow xy\le1\)
\(1+xy=x^2+y^2\ge-2xy\Rightarrow xy\ge-\dfrac{1}{3}\)
\(P=\left(x^2+y^2\right)^2-x^2y^2-2x^2y^2=\left(x^2+y^2-xy\right)\left(x^2+y^2+xy\right)-2x^2y^2\)
\(=x^2+y^2+xy-2x^2y^2=-2x^2y^2+2xy+1\)
Đặt \(a=xy\Rightarrow P=f\left(a\right)=-2a^2+2a+1\)
Xét hàm \(f\left(a\right)=-2a^2+2a+1\) trên \(\left[-\dfrac{1}{3};1\right]\)
\(-\dfrac{b}{2a}=\dfrac{1}{2}\in\left[-\dfrac{1}{3};1\right]\)
\(f\left(-\dfrac{1}{3}\right)=\dfrac{1}{9}\) ; \(f\left(\dfrac{1}{2}\right)=\dfrac{3}{2}\) ; \(f\left(1\right)=1\)
\(\Rightarrow M=\dfrac{3}{2}\) ; \(m=\dfrac{1}{9}\) \(\Rightarrow Mm=\dfrac{1}{6}\)
Đúng 4
Bình luận (0)
Cho 2 số dương x,y thay đổi nhưng luôn thỏa mãn điều kiện \(\frac{2}{x}+\frac{3}{y}=6\)
Tính giá trị nhỏ nhất của biểu thức x+y
Cho x, y là hai số thực dương thay đổi và thỏa mãn điều kiện x + 2y - xy 0. Tìm giá trị nhỏ nhất của biểu thức
P
x
2
4
+
8
y
+
y
2
1
+
x
A.
8
5
B.
5...
Đọc tiếp
Cho x, y là hai số thực dương thay đổi và thỏa mãn điều kiện x + 2y - xy = 0. Tìm giá trị nhỏ nhất của biểu thức P = x 2 4 + 8 y + y 2 1 + x
A. 8 5
B. 5 8
C. 4 5
D. 5 4
Ta có
P = x 2 4 + 8 y + y 2 1 + x = x 2 4 + 8 y + 2 y 2 4 + 4 x ≥ x + 2 y 2 8 + 4 x + 2 y
Dấu “=” xảy ra khi x = 2y
Đặt t = x + 2y; t ≥ 8 . Khi đó P ≥ t 2 8 + 4 t
Xét hàm số f t = t 2 8 + 4 t , t ∈ [ 8 ; + ∞ )
Suy ra f(t) đồng biến trên [ 8 ; + ∞ ) nên f t ≥ f 8 = 8 5 Vậy m a x P = 8 5 ⇔ x = 4 ; y = 2
Đáp án A
Đúng 0
Bình luận (0)
Bài 1:Cho số thực x. Với xge1.Tìm giá trị nhỏ nhất của biểu thứcAsqrt{x-2sqrt{x-1}}+5.sqrt{x+3-4.sqrt{x-1}}+sqrt{x+8-6.sqrt{x-1}}Bài 2:Tìm giá trị lớn nhất và giá trị nhỏ nhất của biểu thức:yfrac{x^2}{x^2-5x+7}Bài 3:Cho hai số dương x,y thay đổi nhưng luôn thỏa mãn điều kiện frac{2}{x}+frac{3}{y}6Tìm giá trị nhỏ nhất của x+y
Đọc tiếp
Bài 1:
Cho số thực x. Với \(x\ge1\).Tìm giá trị nhỏ nhất của biểu thức
\(A=\sqrt{x-2\sqrt{x-1}}+5.\sqrt{x+3-4.\sqrt{x-1}}+\sqrt{x+8-6.\sqrt{x-1}}\)
Bài 2:
Tìm giá trị lớn nhất và giá trị nhỏ nhất của biểu thức:
\(y=\frac{x^2}{x^2-5x+7}\)
Bài 3:
Cho hai số dương x,y thay đổi nhưng luôn thỏa mãn điều kiện \(\frac{2}{x}+\frac{3}{y}=6\)
Tìm giá trị nhỏ nhất của x+y
Bài 3:
Có:\(6=\frac{\left(\sqrt{2}\right)^2}{x}+\frac{\left(\sqrt{3}\right)^2}{y}\ge\frac{\left(\sqrt{2}+\sqrt{3}\right)^2}{x+y}\Rightarrow x+y\ge\frac{5+2\sqrt{6}}{6}\)
True?
Đúng 0
Bình luận (0)
Bài 2: Thực sự không chắc lắm về cách này
\(y=\frac{x^2}{x^2-5x+7}\Rightarrow x^2\left(y-1\right)-5yx+7y=0\)
Coi pt trên là pt bậc 2 ẩn x, dùng điều kiện có nghiệm của pt bậc 2 ta có \(\Delta=25y^2-28y\left(y-1\right)=28y-3y^2\ge0\Leftrightarrow28y\ge3y^2\)
Xét y âm, chia 2 vế của bất đẳng thức cho y âm ta được \(y\ge\frac{28}{3}\)không thỏa
Xét y dương ta thu được \(y\le\frac{28}{3}\), cái này thì em không không biết có nghiệm x không nhờ mọi người kiểm tra dùm
Vậy Maxy=28/3 còn Miny=0 (cái min thì dễ hà )
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
Cho 3 số thực x, y, z thay đổi thỏa mãn x + y + z = 1. Tìm giá trị nhỏ nhất của biểu thức
\(P=\dfrac{1}{2023xz}+\dfrac{1}{2023yz}\)
\(P=\dfrac{1}{2023}\dfrac{1}{z}\left(\dfrac{1}{x}+\dfrac{1}{y}\right)=\dfrac{1}{2023.z}\dfrac{x+y}{xy}\)
Ap dung BDT cosi taco
\(P\ge\dfrac{1}{2023z}.\dfrac{x+y}{\dfrac{\left(x+y\right)^2}{4}}=\dfrac{4}{2023z}\dfrac{1}{x+y}\)
<->\(P\ge\dfrac{4}{2023}\dfrac{1}{z\left(1-z\right)}=\dfrac{4}{2023}\dfrac{1}{-z^2+z}=\dfrac{4}{2023}\dfrac{1}{-\left(z-\dfrac{1}{2}\right)^2+\dfrac{1}{4}}\)
\(< =>P\ge\dfrac{4}{2023}\dfrac{1}{\dfrac{1}{4}}=\dfrac{16}{2023}\)
\(P_{min}=\dfrac{16}{2023}\Leftrightarrow Z=\dfrac{1}{2},x=y=\dfrac{1}{4}\)
Đúng 1
Bình luận (0)
Cho hai vectơ
a
→
,
b
→
thay đổi nhưng luôn thỏa mãn: Giá trị nhỏ nhất của A. 11 B. -1 C. 1 D. 0
Đọc tiếp
Cho hai vectơ
a
→
,
b
→
thay đổi nhưng luôn thỏa mãn: ![]() Giá trị nhỏ nhất của
Giá trị nhỏ nhất của ![]()
A. 11
B. -1
C. 1
D. 0
Đáp án C
Áp dụng bất đẳng thức vectơ
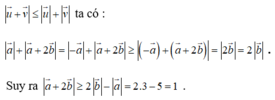
Dấu bằng xảy ra khi 2 vectơ ![]() cùng hướng. Vậy độ dài của vectơ |
a
→
-
2
b
→
| ≥ 0 nhỏ nhất bằng 1.
cùng hướng. Vậy độ dài của vectơ |
a
→
-
2
b
→
| ≥ 0 nhỏ nhất bằng 1.
Suy ra đáp án đúng là C.
Đúng 0
Bình luận (0)