\(^{4^{x+2}+4^{x+1}=1040}\)
LH
Những câu hỏi liên quan
4x+3+4x=1040
4x + 3 + 4x = 1040
4x . 43 + 4x . 1 = 1040
4x ( 43 + 1 ) = 1040
4x . 65 = 1040
4x = 1040 : 65 = 16 = 42
Vậy x = 2
Đúng 3
Bình luận (0)
\(4^{x+3}+4^x=1040\)
\(\Leftrightarrow4^x\left(1+4^3\right)=1040\)
\(\Leftrightarrow4^x.65=1040\)
\(\Leftrightarrow4^x=16\)
\(\Leftrightarrow x=2\)
Đúng 1
Bình luận (0)
Tìm x:
1) \(\left(4x-7\right)^2-5\times\left|7-4x\right|=0\)
2) \(4^{x-2}+4^{x+1}=1040\)
1) (4x−7)2−5×|7−4x|=0
Có (4x-7)2 \(\ge0\) với mọi x
|7−4x| \(\ge0\) với mọi x
<=> 5|7−4x| \(\ge0\) với mọi x
Để (4x−7)2−5×|7−4x|=0 thì \(\left\{{}\begin{matrix}\left(4x-7\right)^2=0\\5|7-4x|=0\end{matrix}\right.\)<=>\(\left\{{}\begin{matrix}4x-7=0\\7-4x=0\end{matrix}\right.\)<=>\(\left\{{}\begin{matrix}4x=7\\4x=7\end{matrix}\right.\)<=>\(x=\dfrac{7}{4}\)
Vậy \(x=\dfrac{7}{4}\)
Đúng 0
Bình luận (0)
2) \(4^{x-2}+4^{x+1}=1040\)
<=> \(4^{x+1}.4^{-3}+4^{x+1}=1040\)
<=> \(4^{x+1}\left(4^{-3}+1\right)=1040\)
<=> \(4^{x+1}.\dfrac{65}{64}=1040\)
<=> \(4^{x+1}=1024=4^5\)
=> x+1=5 <=> x=4
Vậy x=4
Đúng 0
Bình luận (0)
Các bạn giúp tôi nha Mai tôi nộp rùi Thanks
Tìm số thực của x
a)(4x-7)\(^2\)----5|7-4x|=0
b)\(\sqrt{16\left(x-1\right)}\)----\(\sqrt{9x-9}\)=5
c)4\(^{x-2}\)+4\(^{x+1}\)=1040
\(\sqrt{4x^2-4x+1}-\sqrt{4x^2+4x+1}\)
Ta có: \(\sqrt{4x^2-4x+1}-\sqrt{4x^2+4x+1}\)
\(=\sqrt{\left(2x-1\right)^2}-\sqrt{\left(2x+1\right)^2}\)
\(=\left|2x-1\right|-\left|2x+1\right|\)
Đúng 1
Bình luận (0)
`c)(2x-1)^{2}+(1-x).3x<=(x+2)^{2}`
`<=>>4x^{2}-4x+1+3x-3x^{2}<=x^{2}+4x+4`
`<=>x^{2}-x+1<=x^{2}+4x+4`
`<=>4x+x>=1-4`
`<=>5x>=-3`
`<=>x>=-3/5`
thứ nhất bn đăng sai môn
thứ hai bn giải r đăng lmj :???
Đúng 1
Bình luận (0)
Thứ nhất đang sai môn
Thứ hai không biết giải fndf]-0jhdfuhiofghjfgoihjfgopihjfgihjohjgo;hjghghgdjhldhjdfighjs;dligjlkdfgjdhfghfgh41fg6j541fg3j5h4gf6j54dgh65gf4654j
5gj5fg
35j4gh
6jfd4
5j4fj
phân tích đa thức thành nhân tử
1. 4x^2-4x+1
2. 4x^2-4x-3
\(4x^2-4x+1=\left(2x\right)^2-2.2x.1+1^2=\left(2x-1\right)^2\\ ---\\ 4x^2-4x-3\\ =4x^2-4x+1-4\\ =\left(2x-1\right)^2-2^2=\left(2x-1-2\right)\left(2x-1+2\right)\\ =\left(2x-3\right)\left(2x+1\right)\)
Đúng 2
Bình luận (0)
1: =(2x)^2-2*2x*1+1^2
=(2x-1)^2
2: =4x^2-6x+2x-3
=2x(2x-3)+(2x-3)
=(2x-3)(2x+1)
Đúng 1
Bình luận (0)
1 Rút gọn biểu thức
(4x+1)^2+(4x-1)^2-2(4x+1)(4x-1)
2 Phân tích đa thức thành nhân tử
4x^2-9+(2x+3)
1) ( 4x + 1 )2 + ( 4x - 1 )2 - 2( 4x + 1 ).( 4x - 1 )
= ( 4x + 1 - 4x - 1 )2
= 22
= 4
2) 4x2 - 9 + ( 2x + 3 )
= ( 2x )2 - 32 + ( 2x + 3 )
= ( 2x + 3 ).( 2x - 3 ) + ( 2x + 3 )
= ( 2x + 3 ). ( 2x - 3 + 1 )
= ( 2x + 3 ) .( 2x - 2 )
= 2.( 2x + 3 ) .( x - 1 )
Đúng 0
Bình luận (0)
1, (4x+1)^2 + (4x-1)^2 - 2(4x+1)(4x-1)
=[(4x+1)-(4x-1)]^2
=(4x+1-4x+1)^2
=2^2
=4
2, 4x^2 - 9 +(2x+3)
=(4x^2 - 9)+(2x+3)
=(2x+3)(2x-3)+(2x+3)
=(2x+3)(2x-3+1)
=(2x+3)(2x-2)
=2(x-1)(2x+3)
=.= hok tốt!!
Đúng 0
Bình luận (0)
rút gọn biểu thức
(4x+1)^2+(4x-1)^-2(4x+1)(4x-1)
a, Vẽ đồ thị hàm số y= \(\sqrt{4x^2-4x+1}\) + \(\sqrt{x^{2^{ }}-4x+4}\)
b, Biện luận theo m số nghiệm của phương trình:
\(\sqrt{4x^{2^{ }}-4x+1}\)+ \(\sqrt{x^{2^{ }}-4x+4}\) = m
\(y=\sqrt{\left(2x-1\right)^2}+\sqrt{\left(x-2\right)^2}=\left|2x-1\right|+\left|x-2\right|\)
\(y=\left[{}\begin{matrix}3x-3\left(\text{với }x\ge2\right)\\3-3x\left(\text{với }x\le\dfrac{1}{2}\right)\\x+1\left(\text{với }\dfrac{1}{2}\le x\le2\right)\end{matrix}\right.\)
Từ đó ta có đồ thị hàm số như sau:
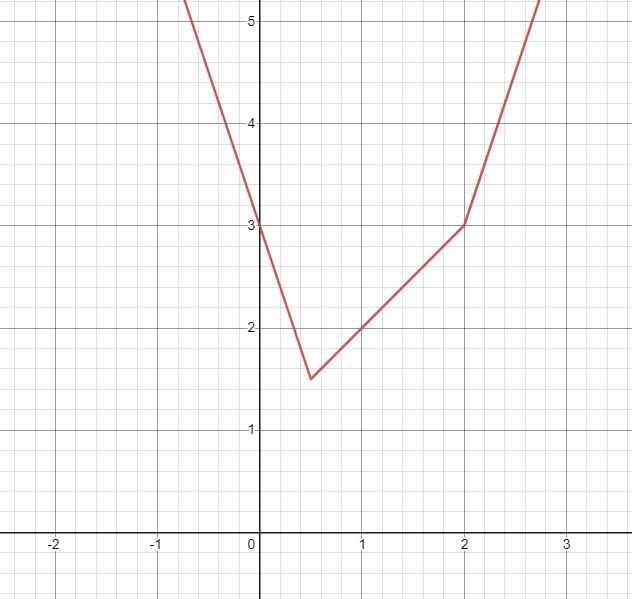
Từ đồ thị ta thấy phương trình \(\sqrt{4x^2-4x+1}+\sqrt{x^2-4x+4}=m\):
- Có đúng 1 nghiệm khi \(m=\dfrac{3}{2}\)
- Có 2 nghiệm phân biệt khi \(m>\dfrac{3}{2}\)
- Vô nghiệm khi \(m< \dfrac{3}{2}\)
Đúng 0
Bình luận (0)