cho tứ giác ABCD ,AD=BC. M,N,P,Q là trung điểm AB,AC,DC,BD a. c/mMNPQ là hình thoi b. cho góc D=50 ,C=70.c/m QPN=60 ,QN=1/2AD c. cho MPgiao DA tại E và CP ở F.c/m DEP=CEF
NA
Những câu hỏi liên quan
Cho hình bình hành ABCD, M là trung điểm AB, N là trung điểm CD.
a. CM tứ giác AMND là hình bình hành.
b. CM Tứ giác AMCN là hình bình hành.
c. CM AC,BD, MN đồng quy.
Bài 2 : Cho hình thang cân ABCD ( AB // CD ). Gọi M,N,P ,Q lần lượt là trung điểm Ab,CD,AD,CA. Biết AC vuông góc với BD.
a. CM tứ giác MNPQ là hình bình hành.
b. CM tứ giác MNPQ là hình thoi.
Cho tứ diện ABCD. Gọi M, N, P, Q lần lượt là trung điểm AC, BC, BD, AD. Tìm điều kiện để tứ giác MNPQ là hình thoi.
A. AB = BC.
B. BC = AD.
C. AC = BD.
D. AB = CD.
Chọn D.
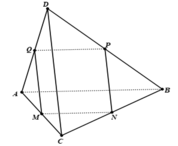
+) Tam giác ABC có MN là đường trung bình nên MN // AB (1).
- Tam giác ABD có PQ là đường trung bình nên PQ // AB (2)
- Từ (1) và (2) suy ra: MN // PQ.
+) Chứng minh tương tự, ta có: MQ// NP (vì cùng // CD)
- Do đó, tứ giác MNPQ là hình bình hành.
+) Để tứ giác MNPQ là hình thoi khi MQ = PQ.
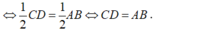
Đúng 0
Bình luận (0)
Cho tứ giác ABCD có BC=AD và BC không song song với AD,gọi M,N,P,Q,E,F lần lượt là trung điểm của các đoạn thẳng AB,BC,CD,DA,AC,BD.
a,C/m tứ giác MEPF là hình thoi
b,C/m MP,NQ,EF đồng quy
Giúp với mn!!
Cho tứ giác ABCD có AB=CD . Gọi E,F,H,Q là trung điểm của AD,AC,BC,BD . Chứng minh tứ giác EFHQ là hình thoi
Xet tam giac ABC ta co : F la trung diem AC *(gt) H la trung diem BC ( gt)===> FH la duong trung binh --> FH// AB va FH=1/2 AB
xet tam giac ABD ta co : E la trung diem AD( gt), Q la trung diem BD (gt)------> EQ la duong trung binh--> EQ//AB va EQ=1/2 AB
ta co : FH//AB (cmt) va EQ//AB (cmt)---> FH// EQ
FH=1/2 AB va EQ=1/2 AB ( cmt)--> FH=EQ
xet tu giac EFHQ ta co : FH// EQ va FH=EQ ( cmt)--> tu giac EFHQ la hbh ( tu giac co 2 cap canh doi vua // vua bang nhau)
Xet tam giac ADC ta co : E la trung diem AD ( gt) , F la trung diem AC ( gt)--> EF la duong trung binh -> EF=1/2 DC
ta co : EF=1/2DC ( cmt)
FH=1/2 AB ( cmt)
AB=DC ( gt)
==> EF = FH
xet hbh EFHQ ta co EF= FH ( cmt)--> tu giac EFHQ la hinh thoi ( tu giac co 2 canh ke bang nhau )
Đúng 0
Bình luận (0)
Cho tứ giác abcd. ac = bd = 10 cm . m là trung điểm của ab , n là trung điểm bc , q là trung điểm của cd , p là trung điểm của ad.
cm : a) mnqp là hình thoi.
b ) ac giao bd tại o. góc aob = 60 độ.Tính diện tích mnqp
cho tứ giác ABCD, có AD=BC và BC không song song với AD. gọi M,N,P,Q,E,F lần lượt là trung điểm của các đoạn thẳng AB,BC,CD,DA,AC,BD
chứng minh :
a tứ giác MEPF là hình thoi
b các đoạn thẳng MP,NQ,EF cùng cắt nhau tại 1 điểm
c tìm điều kiện của tứ giác ABCD để N,E,F,Q thẳng hàng
Cho tứ giác ABCD có AD = BC. Gọi E, F, M, N lần lượt là trung điểm AB, CD, BD, AC. Chứng minh tứ giác EMFN là hình thoi. mn giúp mik với plsss![]()
![]()
Xét ΔABC có
E là trung điểm của AB
N là trung điểm của AC
Do đó: EN là đường trung bình của ΔABC
Suy ra: EN//BC và \(EN=\dfrac{BC}{2}\left(1\right)\)
Xét ΔBDC có
M là trung điểm của BD
F là trung điểm của CD
Do đó: MF là đường trung bình của ΔBDC
Suy ra: MF//BC và \(MF=\dfrac{BC}{2}\left(2\right)\)
Xét ΔABD có
E là trung điểm của AB
M là trung điểm của BD
Do đó: EM là đường trung bình của ΔABD
Suy ra: \(EM=\dfrac{AD}{2}=\dfrac{BC}{2}\left(3\right)\)
Từ (1) và (2) suy ra EN//MF và EN=MF
Từ (1) và (3) suy ra EN=EM
Xét tứ giác ENFM có
EN//MF
EN=MF
Do đó: ENFM là hình bình hành
mà EN=EM
nên ENFM là hình thoi
Đúng 0
Bình luận (0)
)
Cho tứ giác ABCD có BC = AD và BC không song song với AD, gọi M, N, P, Q, E, F lần lượt là trung điểm của các đoạn thẳng AB, BC, CD, DA, AC, BD. a/ (1,25đ) Chứng minh tứ giác MEPF là hình thoi . b/ (1,25đ)Chứng minh các đoạn thẳng MP, NQ, EF cùng cắt nhau tại một điểm . c/ (0,5đ) Tìm thêm điều kiện của tứ giác ABCD để N, E, F, Q thẳng hàng .
Cho hình thoi ABCD góc A nhọn. Gọi M,N,P,Q, lần lượt là trung điểm của các cạnh AB,BC,CD,DA
a, Tứ giác MNPQ là hình gì ? Vì sao
b, Để tứ giác MNPQ là hình vuông thì hình thoi ABCD cần có điều kiện gì ?
c, Cho AC = 34cm, BD = 25cm. Hãy tính diện tích tứ giác MNPQ


