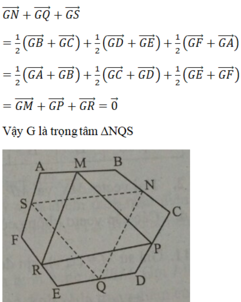
cho lục giác ABCDEF, M, N lần lượt là trung điểm của EF, BD. CMR: tam giác AMN đều
BT
Những câu hỏi liên quan
cho lục giác đều abcdef các điểm m, n, p lần lượt là trung điểm các cạnh ab ,cd ,ef . cmr mnp là tam giác đều
cho lục giác đều ABCDEF, M là trung điểm của EF, N là trung điểm của BD
C/M \(\Delta\) AMN đều
Giải thích các bước giải:
Gọi I trung điểm CD ⇒ NI=ME và NI//ME
⇒ NIEM hình bình hành.
⇒ IE=NM. Mặt khác: IE=MD (IDEM thang cân do CFED thang cân) và MD=AM (đối xứng) nên NM=AM(1).
Ta có: tam giác ONE= tam giác IDE (vì NO=ID; DE=OE; ∠ NOE= ∠ IDE) ⇒ NE=IE mà NE=NA ( đối xứng) ⇒ AN=IE=NM(2)
Từ (1) và (2)⇒ AM=AN=KM hay tam giác ANM đều.
cho lục giác đều ABCDEF. M, N, P lần lượt là trung điểm các cạnh AB, CD, EF.CMR: tam giác MNP đều
Cho lục giác ABCDEF. Gọi M, N, P, Q, S lần lượt là trung điểm của các cạnh AB, BC, CD, DE, EF, FA. Chứng minh rằng hai tam giác MPR và NQS có cùng trọng tâm ?
Giải:
Gọi \(G\) là trọng tâm của \(\Delta MPR\) và \(K\) là trọng tâm của của \(\Delta NQS\)
\(\Rightarrow\) Ta cần chứng minh: \(K\) và \(G\) trùng nhau
Vì \(G\) là trọng tâm của \(\Delta MPR\) nên ta có:
\(3\overrightarrow{KG}=\overrightarrow{KM}+\overrightarrow{KP}+\overrightarrow{KR}\)
\(=\dfrac{1}{2}\left(\overrightarrow{KA}+\overrightarrow{KB}+\overrightarrow{KC}+\overrightarrow{KD}+\overrightarrow{KE}+\overrightarrow{KF}\right)\) (t/c trung điểm)
\(=\dfrac{1}{2}\left(\overrightarrow{KB}+\overrightarrow{KC}\right)+\dfrac{1}{2}\left(\overrightarrow{KD}+\overrightarrow{KE}\right)+\dfrac{1}{2}\left(\overrightarrow{KA}+\overrightarrow{KF}\right)\)
\(=\overrightarrow{KN}+\overrightarrow{KQ}+\overrightarrow{KS}=\overrightarrow{0}\) (Vì \(K\) là trọng tâm của của \(\Delta NQS\))
\(\Rightarrow\) Đpcm
Đúng 0
Bình luận (0)
Cho lục giác ABCDEF. Gọi M, N, P, Q, R, S lần lượt là trung điểm các cạnh AB, BC, CD, DE, EF, FA. Các cặp tam giác nào sau đây có cùng trọng tâm?
A. MPR và MDE
B. MPR và ABQ
C. MPR và NQS
D. MNR và PQS
Cho lục giác ABCDEF. Gọi M, N, P, Q, R, S lần lượt là trung điểm của các cạnh AB, BC, CD, DE, EF, FE. Chứng minh rằng hai tam giác MPR và NQS có cùng trọng tâm ?
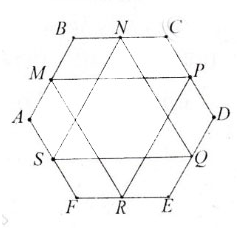
Ta có :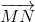 
= 
= 
= 
=> ++ = (++) = 
= 
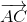
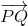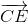
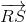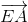
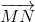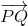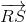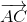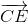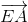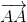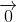
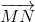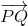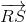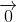=> ++ = (1)
Gọi G là trong tâm của tam giác MPR, ta có:
+ 
+
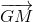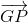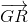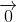= (2)
Mặt khác : =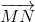 
+
= 
+
= 
+
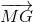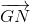
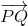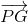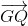
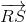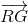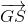
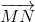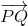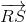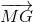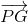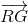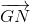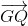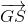=> ++ =(++)+ ++ (3)
Từ (1),(2), (3) suy ra: ++ =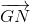
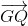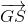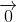
Vậy G là trọng tâm của tam giác NQS
Đúng 0
Bình luận (0)
cho lục giác đều ABCDEF, M là trung điểm của EF, N là trung điểm của BD
C/M \(\Delta\) AMN đều
Vì ABCDEF là lục giác đều →C,O,F thẳng hàng
Gọi I là trung điểm CD
→ΔDIE=ΔOKE(c.g.c)→EI=EK
Mà K,I là trung điểm OC,CD →KI=1\2OD=EM,KI//EM→◊KIEM là hình bình hành
→KM=EI=EK=AK do A,Eđối xứng qua CF
Lại cóΔIDE=ΔMFA(c.g.c)
→EI=AM
→AM=AK=KM
→ΔAKMđều
Đúng 0
Bình luận (0)
Tương tự !:Cho lục giác đều ABCDEF. Gọi M là trung điểm của EF, K là trung điểm của BD. cm tam giác AMK đều câu hỏi 212955 - hoidap247.com
Đúng 0
Bình luận (0)
Cho lục giác ABCDEF. Gọi M, N, P, Q, R, S lần lượt là trung điểm các cạnh AB, BC, CD, DE, EF, FA. Chứng minh rằng hai tam giác MPR và NQS có cùng trọng tâm.
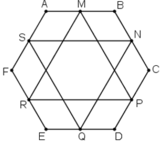
Gọi G là trọng tâm tam giác MPR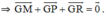 
Ta cần đi chứng minh G cũng là trọng tâm của ΔNQS bằng cách chứng minh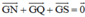 
Thật vậy ta có:
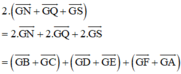
(Vì N, Q, S lần lượt là trung điểm của BC, DE, FA)
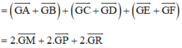
(Vì M, P, R là trung điểm AB, CD, EF)
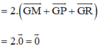
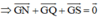hay G cũng là trọng tâm của ΔNQS.
Vậy trọng tâm ΔMPR và ΔNQS trùng nhau.
Đúng 0
Bình luận (0)
Cho lục giác ABCDEF. Gọi M, N, P, Q, R, S lần lượt là trung điểm của các cạnh AB, BC, CD, DE, EF, FA. Chứng minh rằng hai tam giác MPR và NQS có cùng trọng tâm.
Ta có : =
=
=
=> +
+
=
(
+
+
) =
=
=> +
+
=
(1)
Gọi G là trong tâm của tam giác MPR, ta có:
+
+
=
(2)
Mặt khác : =
+
=
+
=
+
=> +
+
=(
+
+
)+
+
+
(3)
Từ (1),(2), (3) suy ra: +
+
=
Vậy G là trọng tâm của tam giác NQS
Đúng 0
Bình luận (0)