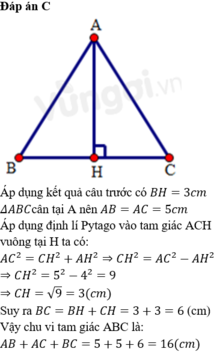
Cho tam giác ABC cân tại A có AB=5cm; BC=6cm. Kẻ phân giác trong AM(M \(\in\)BC). Gọi O là trung điểm BC và K là điểm đối xứng của M qua O
a) Tính diện tích tam giác ABC
b) Tứ giác ABMO là hình gì? Vì sao?
c) Để tứ giác AMCK là hình vuông thì tam giác ABC phải có thêm điều kiện gì?