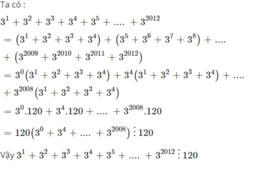Cho A=31+32+33+34+35+....32019.Tìm x để 2a+3=3x
Tuyển Cộng tác viên Hoc24 nhiệm kì 26 tại đây: https://forms.gle/dK3zGK3LHFrgvTkJ6
NN
Những câu hỏi liên quan
Cho A =32019:1+3+32+33+.......+32018 tìm A
A=32019+1+3+32+33+...+32018
⇒A=1+3+32+...+32018+32019
⇒3A=3×(1+3+3^2+3^3+....+3^2019)
3A=3+3^2+3^3+....+3^2020
3A-A=(3+3^2+3^3+....+3^2020) -(1+3+3^2+....+3^2019)
2A= 3^2020-1
⇒ A =( 3^2020-1):2
Đúng 0
Bình luận (0)
A=32019+1+3+32+33+...+32018
⇒A=1+3+32+...+32018+32019
⇒3A=3×(1+3+3^2+3^3+....+3^2019)
⇒3A=3+3^2+3^3+....+3^2020
⇒3A-A=(3+3^2+3^3+....+3^2020) -(1+3+3^2+....+3^2019)
⇒2A= 3^2020-1
⇒ A =( 3^2020-1):2
Đúng 0
Bình luận (0)
a) Cho A = 3 + 32 + 33 + 34 +… + 3100
Tìm số tự nhiên n để: 2A + 3 = 34n+1
b) Tìm các số nguyên tố x, y thỏa mãn: x2 + 1 = 6y2 + 2
a) Cho A = 3 + 32 + 33 + 34 +… + 3100
Tìm số tự nhiên n để: 2A + 3 = 34n+1
b) Tìm các số nguyên tố x, y thỏa mãn: x2 + 1 = 6y2 + 2
a) Cho A = 3 + 32 + 33 + 34 +… + 3100
Tìm số tự nhiên n để: 2A + 3 = 34n+1
b) Tìm các số nguyên tố x, y thỏa mãn: x2 + 1 = 6y
Mọi người cứu với
\(a,A=3+3^2+3^3+3^4+...+3^{100}\\ 3A=3^2+3^3+3^4+3^5+3^{101}\\ 3A-A=2A=3^{101}-3\\ \Rightarrow2A+3=3^{101}=3^{4.25+1}\\ \Rightarrow n=25\)
Đúng 2
Bình luận (0)
cho A = 31 + 32 + 33 + 34 +35 +...... +32012
Chứng minh A chia hết cho "120"
\(A=3+3^2+3^3+...+3^{2012}\\ A=\left(3+3^2+3^3+3^4\right)+...+\left(3^{2009}+3^{2010}+3^{2011}+3^{2012}\right)\\ A=120+...+3^{2008}.120\\ A=120.\left(1+...+3^{2008}\right)⋮120\)
Đúng 1
Bình luận (2)
\(=\left(3+3^2+3^3+3^4\right)+...+3^{2008}\left(3+3^2+3^3+3^4\right)\)
\(=120+...+3^{2008}.120=120\left(1+...+3^{2008}\right)⋮120\)
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
So sánh: 31/32+32/33+35/34 và 31+32+35/34
Giúp mình với nha. Thanks nhìu
ta có: \(\frac{31+32+35}{34}=\frac{31}{34}+\frac{32}{34}+\frac{35}{34}.\)
mà \(\frac{31}{32}>\frac{31}{34};\frac{32}{33}>\frac{32}{34}\)
\(\Rightarrow\frac{31}{32}+\frac{32}{33}+\frac{35}{34}>\frac{31}{34}+\frac{32}{34}+\frac{35}{34}=\frac{31+32+35}{34}\)
Đúng 0
Bình luận (0)
Bài 1: Tìm ƯCLN sau đó suy ra ƯC của các số sau: a) 24, 36, 42 b) 11, 33 Bài 2: Tìm x biết: a) 27 ⋮ 𝑥 và x > 2. b) x ⋮ 5 và 12 < x ≤ 34 Bài 3: Bác Lan mua 40 quả cam và 60 quả táo để chia thành các giỏ. Biết số quả cam và táo ở các giỏ là như nhau. Hỏi bác Lan chia được nhiều nhất thành bao nhiêu giỏ. *Bài 4: Cho A = 3 + 31 + 32 + 33 + 34 + 35 Chứng minh rằng A là một bội của 4..
Cho A = 1 +3 + 32 + 33 + …..+ 32018 + 32019. Chứng tỏ rằng A ⋮ 4
\(A=1+3+3^2+3^3+...+3^{2018}+3^{2019}\)
\(=\left(1+3\right)+3^2\left(1+3\right)+...+3^{2018}\left(1+3\right)\)
\(=\left(1+3\right)\left(1+3^2+...+3^{2018}\right)\)
\(=4\left(1+3^2+...+3^{2018}\right)\) ⋮4
⇒A⋮4
Đúng 0
Bình luận (0)
3/cho A=3+32+33+34+...+32020
Tìm x biết 2A+3=3X
giúp mình với.
\(\Rightarrow3A=3^2+3^3+3^4+...+3^{2021}\\ \Rightarrow3A-A=3^2+3^3+...+3^{2021}-3-3^2-3^3-...-3^{2020}\\ \Rightarrow2A=3^{2021}-3\\ \Rightarrow2A+3=3^{2021}=3^x\\ \Rightarrow x=2021\)
Đúng 0
Bình luận (0)
Bài 4 : (0.5 điểm) Cho A = 1 +3 + 32 + 33 + …..+ 32018 + 32019. Chứng tỏ rằng A ⋮4
\(A=\left(1+3\right)+3^2\left(1+3\right)+...+3^{2018}\left(1+3\right)\)
\(=4\left(1+3^2+...+3^{2018}\right)⋮4\)
Đúng 1
Bình luận (0)