Chia hai vế cho 12 x ( 12 x  > 0), ta được:

4 3 / 4 x  + 1 − 3 4 / 3 x  = 0

Đặt t =  3 / 4 x  (t > 0), ta có phương trình:

4t + 1 − 3/t = 0 ⇔ 4 t 2  + t − 3 = 0

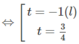
Do đó,  3 / 4 x  =  3 / 4 1 . Vậy x = 1.

1) \(x^2\left(x-1\right)+16\left(1-x\right)\)

\(=x^2\left(x-1\right)-16\left(x-1\right)\)

\(=\left(x^2-16\right)\left(x-1\right)\)

\(=\left(x^2-4^2\right)\left(x-1\right)\)

\(=\left(x-4\right)\left(x+4\right)\left(x-1\right)\)

2)\(81x^2-6yz-9y^2-z^2\)

\(=81x^2-9y^2-6yz-z^2=81x^2-\left(9y^2+6yz+z^2\right)=81x^2-\left(\left(3y\right)^2+6yz+z^2\right)\)

\(=81x^2-\left(3y+z\right)^2=\left(9x\right)^2-\left(3y+z\right)^2\)

\(=\left(9x+3y+z\right)\left(9x-\left(3y+z\right)\right)=\left(9x+3y+z\right)\left(9x-3y-z\right)\)

3)\(xz-yz-x^2+2xy+y^2\)

\(=z\left(x-y\right)-\left(x^2-2xy+y^2\right)\)

\(=z\left(x-y\right)-\left(x-y\right)^2=\left(z+x-y\right)\left(x-y\right)\)

1.(a²+2ab+b²)+(a+b)³=(a+b)²+(a+b)²(a+b)=(a+b)²(a+b+1)

2.x^m+2-x^m=2

3.16x³-54y³=2(8x³-27y³)=2[(2x)³-(3y)³ ]=2(2x-3y)(4x²+6xy+9y²)

\(x^2+4x+4\)

\(=\left(x+2\right)^2\)

\(\left(x-3\right)\left(x^2+3x+9\right)\)

\(=x^3-27\)

\(x^2-4x+4\)

\(=\left(x-2\right)^2\)

2:

a: y1+y2=-(x1+x2)=-5

y1*y2=(-x1)(-x2)=x1x2=6

Phương trình cần tìm có dạng là;

x^2+5x+6=0

b: y1+y2=1/x1+1/x2=(x1+x2)/x1x2=5/6

y1*y2=1/x1*1/x2=1/x1x2=1/6

Phương trình cần tìm là:

a^2-5/6a+1/6=0

`x^2 + 2(m-1)x + m^2 = 0`

Thay `m=0` vào pt và giải ta được :

`x^2 - 6x + 16 = 0`

Vì `x^2 - 6x + 16 > 0` với mọi `x`

`=>` vô nghiệm 

Vậy `S = RR`

Thay `m=-4` vào pt và giải ta được :

`x^2 + 10x + 16 = 0`

`\Delta = 10^2 - 4*1*16 = 36 > 0`

`=> \sqrt{\Delta} = 6`

`=>` Phương trình có 2 nghiệm phân biệt :

`x_1 = (-10+6)/(2*1) = -2`

`x_2 = (-10-6)/(2*1) = -8`

Vậy `S = {-2,-8}`

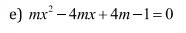
\(\text{∆}=\left(-4m\right)^2-4.m.\left(4m-1\right)\)

\(=16m^2-16m^2+4m\)

\(=4m\)

phương trình vô nghiệm khi \(\text{∆}< 0\)

\(\Rightarrow4m< 0\) 

⇒ \(m< 0\)

`\Delta'=(-2m)^2-m(4m-1)=4m^2-4m^2+m=m`
Để phương trình vô nghiệm thì `\Delta'<0 => m<0`

nhận xét , đánh giá việc thực hành tiết kiệm của bản thân và những người xung quanh , phê phán những biểu hiện lãng phí

a.Bạn thế vào nhé

b.\(\Delta=3^2-4m=9-4m\)

Để pt vô nghiệm thì \(\Delta< 0\)

\(\Leftrightarrow9-4m< 0\Leftrightarrow m>\dfrac{9}{4}\)

c.Ta có: \(x_1=-1\)

\(\Rightarrow x_2=-\dfrac{c}{a}=-m\)

d.Theo hệ thức Vi-ét, ta có:

\(\left\{{}\begin{matrix}x_1+x_2=-3\\x_1.x_2=m\end{matrix}\right.\)

1/ \(x_1^2+x_2^2=34\)

\(\Leftrightarrow\left(x_1+x_2\right)^2-2x_1x_2=34\)

\(\Leftrightarrow\left(-3\right)^2-2m=34\)

\(\Leftrightarrow m=-12,5\)

..... ( Các bài kia tương tự bạn nhé )