Cho cotα =-3/5.Tính các giá trị lượng giác còn lại của góc α
H24
Những câu hỏi liên quan
Tính các giá trị lượng giác của góc α, biết
cotα = 4tanα khi π/2 < α < π
Với π/2 < α < π thì sinα > 0, cosα < 0, tanα < 0
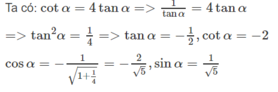
Đúng 0
Bình luận (0)
Cho góc nhọn α. Tính tỉ số lượng giác còn lại nếu cotα= 40/9
\(cot\alpha=\dfrac{40}{9}\Rightarrow tan\alpha=\dfrac{1}{cot\alpha}=\dfrac{1}{\dfrac{40}{9}}=\dfrac{9}{40}\)
+) \(\dfrac{1}{cos^2\alpha}=1+tan^2\alpha\)
\(\Leftrightarrow\dfrac{1}{cos^2\alpha}=1+\left(\dfrac{9}{40}\right)^2\\ \Rightarrow cos\alpha=\sqrt{1:\left(1+\left(\dfrac{9}{40}\right)^2\right)}=\dfrac{40}{41}\)
+) \(sin^2\alpha=1-cos^2\alpha\)
\(\Leftrightarrow sin\alpha=\sqrt{1-cos^2\alpha}=\sqrt{1-\left(\dfrac{40}{41}\right)^2}=\dfrac{9}{41}\)
Đúng 2
Bình luận (0)
Cho cosα=\(\dfrac{1}{3}\) với 0<α<\(\dfrac{\pi}{2}\).Tính các giá trị lượng giác còn lại của góc α.
Em 2k8 ms học nên k chắc
Vì 0 < \(\alpha< \dfrac{\pi}{2}\) => sin \(\alpha>0\)
Cos \(\alpha=\dfrac{1}{3}\) \(\Rightarrow sin\alpha=\sqrt{1-\dfrac{1}{9}}=\dfrac{2\sqrt{2}}{3}\)
tan \(\alpha=2\sqrt{2}\) ; cot \(\alpha=\dfrac{1}{2\sqrt{2}}\)
Đúng 3
Bình luận (1)
Tính các giá trị lượng giác còn lại của góc
α
biết
sin
α
3
5
A.
cos
α
3
4
;
tan
α
3
4
;
c
o
t
α
4
5...
Đọc tiếp
Tính các giá trị lượng giác còn lại của góc α biết sin α = 3 5
A. cos α = 3 4 ; tan α = 3 4 ; c o t α = 4 5
B. cos α = 4 5 ; tan α = 3 4 ; c o t α = 4 3
C. cos α = 4 5 ; tan α = 3 4 ; c o t α = 4 5
B. cos α = 3 4 ; tan α = 4 5 ; c o t α = 4 3
Ta có sin α = 3 5 suy ra sin 2 α = 9 25 , mà sin 2 α + cos 2 α = 1 , do đó:
cos 2 α = 1 - sin 2 α = 1 - 9 25 = 16 25 suy ra cos α = 4 5
Do đó:
tan α = sin α cos α = 3 5 : 4 5 = 3 5 . 5 4 = 3 4
c o t α = cos α sin α = 4 5 : 3 5 = 4 5 . 5 3 = 4 3
Vậy cos α = 4 5 ; tan α = 3 4 ; c o t α = 4 3
Đáp án cần chọn là: B
Đúng 0
Bình luận (0)
Nhắc lại khái niệm giá trị lượng giác của góc α, 0o ≤ α ≤ 180o.
Ta có thể mở rộng khái niệm giá trị lượng giác cho các cung và góc lượng giác.
Các số sinα; cosα; tanα; cotα được gọi là giá trị lượng giác của góc α, với 0o ≤ α ≤ 180o.
Đúng 0
Bình luận (0)
Hãy nhắc lại định nghĩa giá trị lượng giác của một góc α với 0o ≤ α ≤ 180o. Tại sao khi α là các góc nhọn thì giá trị lượng giác này lại chính là các tỉ số lượng giác đã được học ở lớp 9?
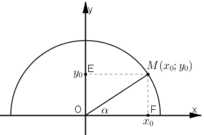
a) Trên nửa đường tròn lượng giác nằm phía trên trục hoành, xác định điểm M(x0; y0) sao cho 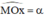
Khi đó ta có:
sin α = y0
cos α = x0
tan α = y0 / x0
cot α = x0 / y0
b) Gọi E, F là hình chiếu của M trên Oy, Ox.
Khi α < 90º thì x0 > 0, y0 > 0
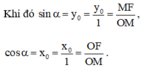
Đúng 0
Bình luận (0)
Cho góc α thỏa mãn
π
2
a
2
π
và
c
o
t
α
+
π
3
-
3
Tính giá trị của biểu thức
P
sin
α
+
π
6...
Đọc tiếp
Cho góc α thỏa mãn π 2 < a < 2 π và c o t α + π 3 = - 3 Tính giá trị của biểu thức P = sin α + π 6 + c o s α
A. P = 3 2
B. P = 1
C. P = -1
D. P = - 3 2
10, Cho t/giác ABC vuông tại A có ^ABC= 40. Tính tỉ số lượng giác của ABC.
14, Cho α = 2. Tính các lượng giác còn lại của góc α biết góc α là góc nhọn.
chỉ rõ hộ mk từng cách giải đc ko ạ?
cho sin α bằng 1/3 và π/2 <α<π . Tính giá trị của cosα,tanα,và cotα
Vì \(\dfrac{\pi}{2}< \alpha< \pi\) \(\Rightarrow\) cos \(\alpha\) < 0
\(\Rightarrow\) cos \(\alpha\) = \(-\sqrt{1-sin^2\alpha}\) = \(-\dfrac{2\sqrt{2}}{3}\)
\(\Rightarrow\) tan \(\alpha\) = \(\dfrac{sin\alpha}{cos\alpha}=\dfrac{-\sqrt{2}}{4}\)
\(\Rightarrow\) cot \(\alpha\) = \(\dfrac{1}{tan\alpha}\) = \(-2\sqrt{2}\)
Chúc bn học tốt!
Đúng 1
Bình luận (0)
Cho \(cosa=-\dfrac{2}{5}\) và \(\pi< a< \dfrac{3\pi}{2}\)
a) Tính các giá trị lượng giác còn lại của góc a
b) Giá trị biểu thức P = cos2a - cos\(\left(\dfrac{\pi}{3}-a\right)\)
b)\(P=cos2a-cos(\dfrac{\pi}{3}-a) \\=2cos^2a-1-cos\dfrac{\pi}{3}cosa-sin\dfrac{\pi}{3}sina \\=2.(\dfrac{-2}{5})^2-1-\dfrac{1}{2}.\dfrac{-2}{5}-\dfrac{\sqrt3}{2}.\dfrac{-\sqrt{21}}{5} \\=\dfrac{-24+15\sqrt7}{50}\)
Đúng 1
Bình luận (0)
a, Vì : \(\pi< a< \dfrac{3\pi}{2}\) nên \(cos\alpha< 0\) mà \(cos^2\alpha=1-sin^2\alpha=1-\dfrac{4}{25}=\dfrac{21}{25},\)
do đó : \(cos\alpha=-\dfrac{\sqrt{21}}{5}\)
từ đó suy ra : \(tan\alpha=\dfrac{2}{\sqrt{21}},cot\alpha=\dfrac{\sqrt{21}}{2}\)
Đúng 1
Bình luận (0)






 .
.

