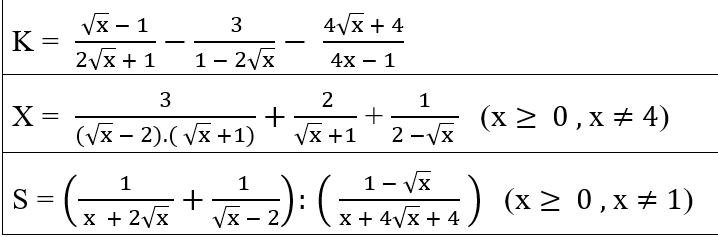
\(X=\dfrac{3}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+1\right)}+\dfrac{2}{\sqrt{x}+1}+\dfrac{1}{2-\sqrt{x}}\left(đk:x\ge0;x\ne4\right)\)

\(X=\dfrac{3}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+1\right)}+\dfrac{2}{\sqrt{x}+1}-\dfrac{1}{\sqrt{x}-2}\)

\(X=\dfrac{3}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+1\right)}+\dfrac{2\left(\sqrt{x}-2\right)}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+1\right)}-\dfrac{\sqrt{x}+1}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+1\right)}\)

\(X=\dfrac{3+2\sqrt{x}-4-\sqrt{x}-1}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+1\right)}\)

\(X=\dfrac{\sqrt{x}-2}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+1\right)}\)

\(X=\dfrac{1}{\sqrt{x}+1}\)

\(S=\left(\dfrac{1}{x+2\sqrt{x}}+\dfrac{1}{\sqrt{x}-2}\right):\left(\dfrac{1-\sqrt{x}}{x+4\sqrt{x}+4}\right)\left(đk:x\ge0;x\ne1\right)\)

\(S=\left(\dfrac{\sqrt{x}-2}{\sqrt{x}\left(\sqrt{x}+2\right)\left(\sqrt{x}-2\right)}+\dfrac{\sqrt{x}\left(\sqrt{x}+2\right)}{\sqrt{x}\left(\sqrt{x}+2\right)\left(\sqrt{x}-2\right)}\right):\left(\dfrac{1-\sqrt{x}}{x+4\sqrt{x}+4}\right)\)

\(S=\dfrac{\sqrt{x}-2+x+2\sqrt{x}}{\sqrt{x}\left(\sqrt{x}+2\right)\left(\sqrt{x}-2\right)}.\dfrac{x+4\sqrt{x}+4}{1-\sqrt{x}}\)

\(S=\dfrac{x+3\sqrt{x}-2}{\sqrt{x}\left(\sqrt{x}+2\right)\left(\sqrt{x}-2\right)}.\dfrac{\left(\sqrt{x}+2\right)^2}{1-\sqrt{x}}\)

\(S=\dfrac{\left(x+3\sqrt{x}-2\right)\left(\sqrt{x}+2\right)}{\sqrt{x}\left(\sqrt{x}-2\right)\left(1-\sqrt{x}\right)}\)

(đến đoạn này thì trong ngoặc ko tách ra đc nữa nên mik nghĩ là đến đây là xong, nếu sai thì bn nói mik)

\(K=\dfrac{\sqrt{x}-1}{2\sqrt{x}+1}-\dfrac{3}{1-2\sqrt{x}}-\dfrac{4\sqrt{x}+4}{4x-1}\left(đk:x\ge0\right)\)

\(K=\dfrac{\sqrt{x}-1}{2\sqrt{x}+1}+\dfrac{3}{2\sqrt{x}-1}-\dfrac{4\sqrt{x}+4}{4x-1}\)

\(K=\dfrac{\left(\sqrt{x}-1\right)\left(2\sqrt{x}-1\right)}{\left(2\sqrt{x}+1\right)\left(2\sqrt{x}-1\right)}+\dfrac{3\left(2\sqrt{x}+1\right)}{\left(2\sqrt{x}+1\right)\left(2\sqrt{x}-1\right)}-\dfrac{4\sqrt{x}+4}{\left(2\sqrt{x}+1\right)\left(2\sqrt{x}-1\right)}\)

\(K=\dfrac{2x-3\sqrt{x}+1}{\left(2\sqrt{x}+1\right)\left(2\sqrt{x}-1\right)}+\dfrac{6\sqrt{x}+3}{\left(2\sqrt{x}+1\right)\left(2\sqrt{x}-1\right)}-\dfrac{4\sqrt{x}+4}{\left(2\sqrt{x}+1\right)\left(2\sqrt{x}-1\right)}\)

\(K=\dfrac{2x-3\sqrt{x}+1+6\sqrt{x}+3-4\sqrt{x}-4}{\left(2\sqrt{x}+1\right)\left(2\sqrt{x}-1\right)}\)

\(K=\dfrac{2x-\sqrt{x}}{\left(2\sqrt{x}+1\right)\left(2\sqrt{x}-1\right)}\)

\(K=\dfrac{\sqrt{x}}{2\sqrt{x}+1}\)

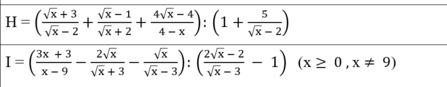
\(H=\dfrac{x+5\sqrt{x}+6+x-3\sqrt{x}+2-4\sqrt{x}+4}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+2\right)}:\dfrac{\sqrt{x}-2+5}{\sqrt{x}-2}\)

\(=\dfrac{2x-2\sqrt{x}+12}{\sqrt{x}+2}\cdot\dfrac{1}{\sqrt{x}+3}\)

\(I=\dfrac{3x+3-2x+6\sqrt{x}-x-3\sqrt{x}}{x-9}:\dfrac{2\sqrt{x}-2-\sqrt{x}+3}{\sqrt{x}-3}\)

\(=\dfrac{3\left(\sqrt{x}+1\right)}{\left(\sqrt{x}-3\right)\left(\sqrt{x}+3\right)}\cdot\dfrac{\sqrt{x}-3}{\sqrt{x}+1}=\dfrac{3}{\sqrt{x}+3}\)

\(P=\left(x-y\right)^2+\left(x+y\right)^2-2\left(x-y\right)\left(x+y\right)-4x^2\\ P=\left(x-y-x-y\right)^2-4x^2\\ P=4y^2-4x^2=4\left(y-x\right)\left(x+y\right)\)

Câu 10:

a: ĐKXĐ: \(\left\{{}\begin{matrix}x\notin\left\{2;-1\right\}\\y\ne-5\end{matrix}\right.\)

\(A=\dfrac{y+5}{x^2-4x+4}\cdot\dfrac{x^2-4}{x+1}\cdot\dfrac{x-2}{y+5}\)

\(=\dfrac{y+5}{y+5}\cdot\dfrac{\left(x^2-4\right)}{x^2-4x+4}\cdot\dfrac{x-2}{x+1}\)

\(=\dfrac{\left(x^2-4\right)\cdot\left(x-2\right)}{\left(x+1\right)\left(x^2-4x+4\right)}\)

\(=\dfrac{\left(x+2\right)\left(x-2\right)\cdot\left(x-2\right)}{\left(x+1\right)\left(x-2\right)^2}=\dfrac{x+2}{x+1}\)

b: \(A=\dfrac{x+2}{x+1}\)

=>A không phụ thuộc vào biến y

Khi x=1/2 thì \(A=\left(\dfrac{1}{2}+2\right):\left(\dfrac{1}{2}+1\right)=\dfrac{5}{2}:\dfrac{3}{2}=\dfrac{5}{2}\cdot\dfrac{2}{3}=\dfrac{5}{3}\)

Câu 12:

a: \(A=\dfrac{x}{x+3}+\dfrac{2x}{x-3}+\dfrac{9-3x^2}{x^2-9}\)

\(=\dfrac{x}{x+3}+\dfrac{2x}{x-3}+\dfrac{9-3x^2}{\left(x+3\right)\left(x-3\right)}\)

\(=\dfrac{x\left(x-3\right)+2x\left(x+3\right)+9-3x^2}{\left(x+3\right)\left(x-3\right)}\)

\(=\dfrac{x^2-3x+2x^2+6x+9-3x^2}{\left(x+3\right)\left(x-3\right)}\)

\(=\dfrac{3x+9}{\left(x+3\right)\left(x-3\right)}=\dfrac{3\left(x+3\right)}{\left(x+3\right)\left(x-3\right)}=\dfrac{3}{x-3}\)

b: Khi x=1 thì \(A=\dfrac{3}{1-3}=\dfrac{3}{-2}=-\dfrac{3}{2}\)

\(x+\dfrac{1}{3}=\dfrac{10}{3}\)

=>\(x=\dfrac{10}{3}-\dfrac{1}{3}\)

=>\(x=\dfrac{9}{3}=3\left(loại\right)\)

Vậy: Khi x=3 thì A không có giá trị

c: \(B=A\cdot\dfrac{x-3}{x^2-4x+5}\)

\(=\dfrac{3}{x-3}\cdot\dfrac{x-3}{x^2-4x+5}\)

\(=\dfrac{3}{x^2-4x+5}\)

\(x^2-4x+5=x^2-4x+4+1=\left(x-2\right)^2+1>=1\forall x\) thỏa mãn ĐKXĐ

=>\(B=\dfrac{3}{x^2-4x+5}< =\dfrac{3}{1}=3\forall x\) thỏa mãn ĐKXĐ

Dấu '=' xảy ra khi x-2=0

=>x=2

Đề bài thiếu thì phải

32, A

33,B

34,C

vẽ lại mạch ta có RAM//RMN//RNB

đặt theo thứ tự 3 R là a,b,c

ta có a+b+c=1 (1)

điện trở tương đương \(\dfrac{1}{R_{td}}=\dfrac{1}{a}+\dfrac{1}{b}+\dfrac{1}{c}\) \(\Rightarrow I=\dfrac{U}{R_{td}}=9.\left(\dfrac{1}{a}+\dfrac{1}{b}+\dfrac{1}{c}\right)\) với a,b,c>0

áp dụng bất đẳng thức cô si cho \(\dfrac{1}{a},\dfrac{1}{b},\dfrac{1}{c}\)  \(\Rightarrow\dfrac{1}{a}+\dfrac{1}{b}+\dfrac{1}{c}\ge\dfrac{3}{\sqrt[3]{abc}}\ge\dfrac{3}{\left(\dfrac{a+b+c}{3}\right)}=\dfrac{9}{a+b+c}=9\)

\(\Leftrightarrow9\left(\dfrac{1}{a}+\dfrac{1}{b}+\dfrac{1}{c}\right)\ge81\Leftrightarrow I\ge81\) I min =81 ( úi dồi ôi O_o hơi to mà vẫn đúng đá nhỉ)

dấu ''='' xảy ra \(\Leftrightarrow a=b=c\left(2\right)\)

từ (1) (2) \(\Rightarrow a=b=c=\dfrac{1}{3}\left(\Omega\right)\)

vậy ... (V LUN MẤT CẢ BUỔI TỐI R BÀI KHÓ QUÁ EM ĐANG ÔN HSG À )

em ơi chụp cả cái mạch điện a xem nào sao chụp nó bị mất r

\(b,\dfrac{\sqrt{12}-\sqrt{6}}{\sqrt{30}-\sqrt{15}}=\dfrac{\sqrt{6}\left(\sqrt{2}-1\right)}{\sqrt{15}\left(\sqrt{2}-1\right)}=\dfrac{\sqrt{6}}{\sqrt{15}}=\dfrac{\sqrt{2}}{\sqrt{5}}\)

\(d,\dfrac{ab-bc}{\sqrt{ab}-\sqrt{bc}}=\dfrac{\left(\sqrt{ab}-\sqrt{bc}\right)\left(\sqrt{ab}+\sqrt{bc}\right)}{\left(\sqrt{ab}-\sqrt{bc}\right)}=\sqrt{ab}+\sqrt{bc}=\sqrt{b}\left(\sqrt{a}+\sqrt{c}\right)\)

\(e,\left(a\sqrt{\dfrac{a}{b}+2\sqrt{ab}}+b\sqrt{\dfrac{a}{b}}\right)\sqrt{ab}\)

\(=a\left(\sqrt{\dfrac{a}{b}+\dfrac{2b.\sqrt{ab}}{b}}+b\sqrt{\dfrac{a}{b}}\right)\sqrt{ab}\)

\(=a\sqrt{a}\sqrt{a+2b\sqrt{ab}}+b\sqrt{a^2}\)

\(=a\sqrt{a^2+2ab\sqrt{ab}}+ab\)

\(=a\left(\sqrt{a^2+2ab\sqrt{ab}}+b\right)\)

\(f,\left(\dfrac{1-a\sqrt{a}}{1-\sqrt{a}}+\sqrt{a}\right)\left(\dfrac{1+a\sqrt{a}}{1+\sqrt{a}}-\sqrt{a}\right)\)

\(=\left(a+\sqrt{a}+1+\sqrt{a}\right)\left(a-\sqrt{a}+1-\sqrt{a}\right)\)

\(=\left(a+2\sqrt{a}+1\right)\left(a-2\sqrt{a}+1\right)\)

\(=\left(\sqrt{a}+1\right)^2\left(\sqrt{a}-1\right)^2\)

\(=\left(a-1\right)^2=a^2-2a+1\)