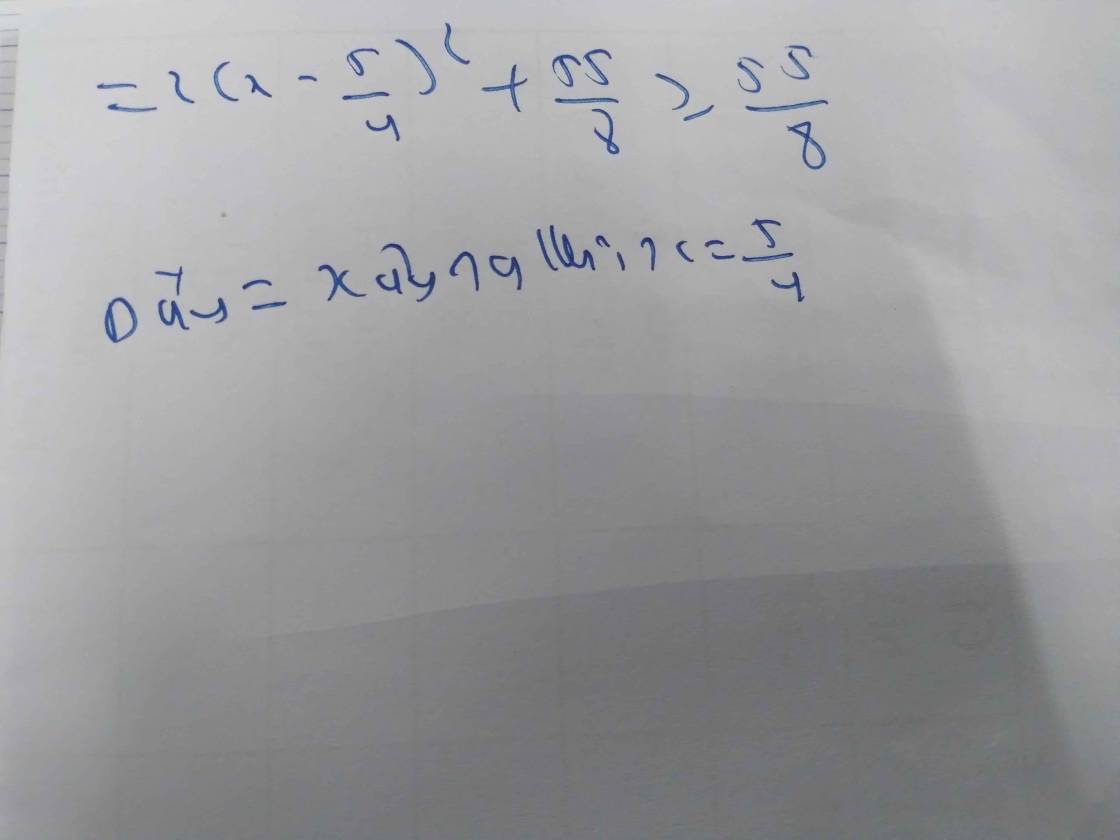\(a,x^2+3x+9\)

\(=x^2+2\cdot x\cdot\dfrac{3}{2}+\left(\dfrac{3}{2}\right)^2+\dfrac{27}{4}\)

\(=\left(x+\dfrac{3}{2}\right)^2+\dfrac{27}{4}\)

Ta thấy: \(\left(x+\dfrac{3}{2}\right)^2\ge0\forall x\)

\(\Rightarrow\left(x+\dfrac{3}{2}\right)^2+\dfrac{27}{4}\ge\dfrac{27}{4}\forall x\)

Dấu \("="\) xảy ra \(\Leftrightarrow x+\dfrac{3}{2}=0\Leftrightarrow x=-\dfrac{3}{2}\)

\(b,2x^2-5x+10\)

\(=2x^2-5x+\dfrac{25}{8}+\dfrac{55}{8}\)

\(=2\left(x^2-2\cdot x\cdot\dfrac{5}{4}+\dfrac{25}{16}\right)+\dfrac{55}{8}\)

\(=2\left(x-\dfrac{5}{4}\right)^2+\dfrac{55}{8}\)

Ta có: \(2\left(x-\dfrac{5}{4}\right)^2\ge0\forall x\)

\(\Rightarrow2\left(x-\dfrac{5}{4}\right)^2+\dfrac{55}{8}\ge\dfrac{55}{8}\forall x\)

Dấu \("="\) xảy ra \(\Leftrightarrow x-\dfrac{5}{4}=0\Leftrightarrow x=\dfrac{5}{4}\)

#\(Toru\)

\(A=\left(x^2-2x+1\right)+4=\left(x-1\right)^2+4\ge4\\ A_{min}=4\Leftrightarrow x=1\\ B=2\left(x^2-3x\right)=2\left(x^2-2\cdot\dfrac{3}{2}x+\dfrac{9}{4}\right)-\dfrac{9}{2}\\ B=2\left(x-\dfrac{3}{2}\right)^2-\dfrac{9}{2}\ge-\dfrac{9}{2}\\ B_{min}=-\dfrac{9}{2}\Leftrightarrow x=\dfrac{3}{2}\\ C=-\left(x^2-4x+4\right)+7=-\left(x-2\right)^2+7\le7\\ C_{max}=7\Leftrightarrow x=2\)

a,\(A=x^2-2x+5=\left(x^2-2x+1\right)+4=\left(x-1\right)^2+4\ge4\)

Dấu "=" \(\Leftrightarrow x=-1\)

b,\(B=2\left(x^2-3x\right)=2\left(x^2-3x+\dfrac{9}{4}\right)-\dfrac{9}{2}=2\left(x-\dfrac{3}{2}\right)^2-\dfrac{9}{2}\ge-\dfrac{9}{2}\)

Dấu "=" \(\Leftrightarrow x=\dfrac{3}{2}\)

c,\(=C=-\left(x^2-4x-3\right)=-\left[\left(x^2-4x+4\right)-7\right]=-\left(x-2\right)^2+7\le7\)

Dấu "=" \(\Leftrightarrow x=2\)

um

a) Để A= I 2x-3 I + 1/2 bé nhất thì I 2x-3 I phải bé nhất, mà   I 2x-3 I bé hơn hoặc = 0=>  I2x-3 I =0 => 2x=3=> x=3/2 

Vậy giá trị nhỏ nhất của A là 1/2 tại x= 3/2

b) Để B nhỏ nhất thì  | 5x + 6 | phải nhỏ nhất, mà  | 5x + 6 | bé hơn hoặc = 0=>  | 5x + 6 |=0 => x= -6/5

Vậy giá trị nhỏ nhất của B là -0.25 tại x=-6/5

c) Để C nhỏ nhất thì Ix-3I hoặc I x+7I phải nhỏ nhất, mà I x-3 I và Ix-7I bé hơn hoặc = 0 => x-3 = 0 hoặc x+7 = 0

=> x=3 hoặc x= -7

Thay x=3 vào C, có:   | 3- 3  | +  | 3 + 7 | = 0+ 10 = 10

Thay x=7 vào C, có:  | -7 - 3  | +  | -7 + 7 | = 10+0 = 10

=> giá trị nhỏ nhất của C là 10 tại x=3 hoặc x=7

\(a,A=x^2-2x+2=\left(x-1\right)^2+1\ge1\)

dấu"=" xảy ra<=>x=1

\(b,B=2x^2-5x+2=2\left(x^2-\dfrac{5}{2}x+1\right)=2\left(x^2-2.\dfrac{5}{4}x+\dfrac{25}{16}-\dfrac{9}{16}\right)\)

\(=2\left[\left(x-\dfrac{5}{4}\right)^2-\dfrac{9}{16}\right]=2\left(x-\dfrac{5}{4}\right)^2-\dfrac{9}{8}\ge-\dfrac{9}{8}\)

dấu"=" xảy ra<=>x=5/4

c,\(C=x^2+2xy+4y^2+3=\left(x+y\right)^2+3\left(y^2+1\right)\ge3\)

dấu"=" xảy ra<=>x=y=0

d,\(D=\left|x-1\right|+|2x-1|=|1-x|+|2x-1|\ge|1-x+2x-1|\)

\(=|x|\ge0\)

dấu"=" xảy ra<=>\(x=0\)