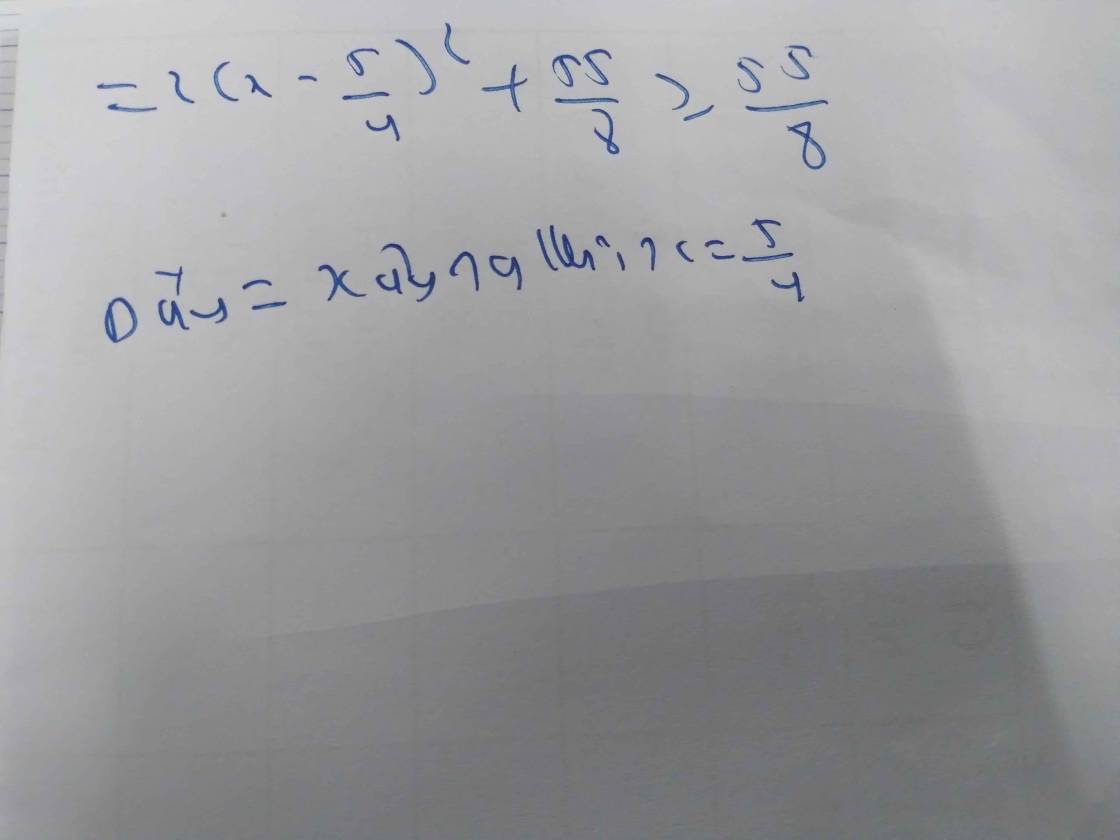\(a,x^2+3x+9\)
\(=x^2+2\cdot x\cdot\dfrac{3}{2}+\left(\dfrac{3}{2}\right)^2+\dfrac{27}{4}\)
\(=\left(x+\dfrac{3}{2}\right)^2+\dfrac{27}{4}\)
Ta thấy: \(\left(x+\dfrac{3}{2}\right)^2\ge0\forall x\)
\(\Rightarrow\left(x+\dfrac{3}{2}\right)^2+\dfrac{27}{4}\ge\dfrac{27}{4}\forall x\)
Dấu \("="\) xảy ra \(\Leftrightarrow x+\dfrac{3}{2}=0\Leftrightarrow x=-\dfrac{3}{2}\)
\(b,2x^2-5x+10\)
\(=2x^2-5x+\dfrac{25}{8}+\dfrac{55}{8}\)
\(=2\left(x^2-2\cdot x\cdot\dfrac{5}{4}+\dfrac{25}{16}\right)+\dfrac{55}{8}\)
\(=2\left(x-\dfrac{5}{4}\right)^2+\dfrac{55}{8}\)
Ta có: \(2\left(x-\dfrac{5}{4}\right)^2\ge0\forall x\)
\(\Rightarrow2\left(x-\dfrac{5}{4}\right)^2+\dfrac{55}{8}\ge\dfrac{55}{8}\forall x\)
Dấu \("="\) xảy ra \(\Leftrightarrow x-\dfrac{5}{4}=0\Leftrightarrow x=\dfrac{5}{4}\)
#\(Toru\)