Giá trị lớn nhất của hàm số y = x ( 5 - 2 x ) 2 trên [0; 3] là:
A. 0
B. 125 27
C. 250 27
D. 250 3
Giá trị lớn nhất của hàm số y = x ( 5 - 2 x ) 2 trên [0; 3] là:
A. 0
B. 125 27
C. 250 27
D. 250 3
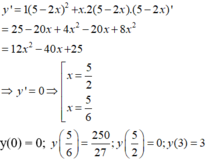
Vậy GTLN của hàm số trên [0; 3] là 250 27 đạt được khi x = 5/6. Chọn đáp án C.
Tổng giá trị lớn nhất và giá trị nhỏ nhất của hàm số y = e x 2 - 2 x + 3 trên đoạn [0 ; 2] là:
A . e 3 -e
B. e 3 + e 2
C . e 3
D. e 3 +e
Gọi M và m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số y = 2 sin x + cos 2x trên đoạn 0 , π . Khi đó 2M + m bằng
A. 4
B. 5/2
C. 7/2
D. 5
Cho hàm số y=f(x) có bảng xét dấu của đạo hàm như sau

Biết rằng f(0)+f(3)=f(2)+f(5) Giá trị nhỏ nhất, giá trị lớn nhất của hàm số f(x) trên đoạn [0;5] lần lượt là
A. f(0), f(5)
B. f(2), f(0)
C. f(1), f(5)
D. f(2), f(5)
Dựa vào bảng xét dấu của f '(x) ta có bảng biến thiên của hàm số trên đoạn [0;5] như sau
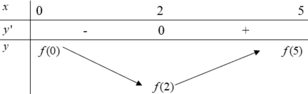
Suy ra ![]() Và
Và ![]()
Ta có ![]()
![]()
Vì f(x) đồng biến trên đoạn [2;5] nên ![]()
⇒ f(5)>f(0)
Vậy
![]()
Chọn đáp án D.
Giá trị lớn nhất của hàm số y = x ( 1 - 2 x ) trên [0; 1/2] là
A. 1
B. 3 4
C. 2 4
D. 6 3
Tìm giá trị lớn nhất của hàm số y = x 3 − 3 x + 5 trên đoạn 0 ; 2 .
A. maxy 0 ; 2 = 3
B. maxy 0 ; 2 = 5
C. maxy 0 ; 2 = 0
D. maxy 0 ; 2 = 7
Đáp án là D.
y ' = 3 x 2 − 3, cho y ' = 0 ⇔ x = 1 ∈ 0 ; 2 x = − 1 ∉ 0 ; 2
y 0 = 5 ; y 2 = 7 ; y 1 = 3.
max 0 ; 2 y = y 2 = 7.
Tìm giá trị lớn nhất của hàm số \(y=x^2-2x+3\) trên đoạn \(\left[0;4\right]\)
\(y=f\left(x\right)=x^2-2x+3\)
\(f\left(0\right)=3;f\left(4\right)=11;f\left(1\right)=2\)
\(\Rightarrow max=f\left(4\right)=11\Leftrightarrow x=4\)
Xét tính đồng biến, nghịch biến và tính giá trị lớn nhất, giá trị nhỏ nhất của hàm số:
a) y = x2 trên đoạn [-3; 0];
b) y = trên đoạn [3; 5].
Cho hàm số y=f(x) liên tục, không âm trên R thỏa mãn f ( x ) . f ' ( x ) = 2 x f ( x ) 2 + 1 và f(0)=0. Giá trị lớn nhất M và giá trị nhỏ nhất m của hàm số y=f(x) trên đoạn [1;3] lần lượt là:
A. M=20;m=2
B. M = 4 11 ; m = 3
C. M = 20 ; m = 2
D. M = 3 11 ; m = 3
Giá trị lớn nhất của hàm số y = x - 2 x + 1 trên đoạn là
A. 2
B. - 1 2
C. 1
D. 0