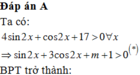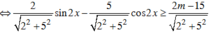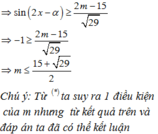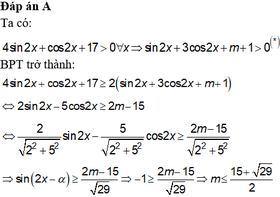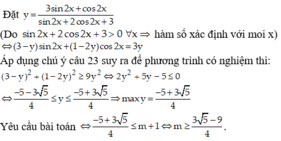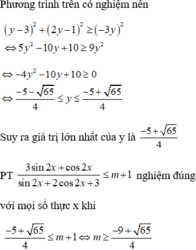41.Tìm m để phương trình y=\(\frac{4sin2x++17}{sin2x+4cos^2x+1}\) đúng với x\(\in\)R
DT
Những câu hỏi liên quan
Tìm m để các bất phương trình
4
sin
2
x
+
cos
2
x
+
17
3
cos
2
x
+
sin
2
x
+
m
+
1...
Đọc tiếp
Tìm m để các bất phương trình 4 sin 2 x + cos 2 x + 17 3 cos 2 x + sin 2 x + m + 1 ≥ 2 đúng với mọi x ∈ R.
A. 10 - 3 < m ≤ 15 - 29 2
B. 10 - 1 < m ≤ 15 - 29 2
C. 10 - 1 < m ≤ 15 + 29 2
D. 10 - 1 < m < 10 + 1
Tìm m để bất phương trình đúng với mọi x ∈ R
\(\frac{4sin2x+cos2x+17}{3cos2x+sin2x+m+1}\ge2\)
\(\Leftrightarrow\frac{4sin2x+cos2x+17}{3cos2x+sin2x+m+1}-2\ge0\) (tất nhiên là với mọi x)
\(\Leftrightarrow\frac{2sin2x-5cos2x-2m+15}{3cos2x+sin2x+m+1}\ge0\)
TH1: \(\left\{{}\begin{matrix}2sin2x-5cos2x-2m+15\ge0\\3cos2x+sin2x+m+1>0\end{matrix}\right.\) ;\(\forall x\)
\(\Leftrightarrow\left\{{}\begin{matrix}\frac{2}{\sqrt{29}}sin2x-\frac{5}{\sqrt{29}}cos2x\ge\frac{2m-15}{\sqrt{29}}\\\frac{1}{\sqrt{10}}sin2x+\frac{3}{\sqrt{10}}cos2x>\frac{-m-1}{\sqrt{10}}\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}sin\left(2x-a\right)\ge\frac{2m-15}{\sqrt{29}}\\sin\left(2x+b\right)>\frac{-m-1}{\sqrt{10}}\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}\frac{2m-15}{\sqrt{29}}\le-1\\\frac{-m-1}{\sqrt{10}}< -1\end{matrix}\right.\) tới đây chắc bạn tự giải được
TH2: tương tự:
\(\left\{{}\begin{matrix}2sin2x-5cos2x-2m+15\le0\\3cos2x+sin2x+m+1< 0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}\frac{2m-15}{\sqrt{29}}\ge1\\\frac{-m-1}{\sqrt{10}}>1\end{matrix}\right.\) \(\Leftrightarrow...\)
Đúng 0
Bình luận (0)
Tìm m để bất phương trình
(
3
sin
x
-
4
cos
x
)
2
-
6
sin
x
+
8
cos
x...
Đọc tiếp
Tìm m để bất phương trình ( 3 sin x - 4 cos x ) 2 - 6 sin x + 8 cos x ≤ 2 m - 1 đúng với mọi x ∈ R .
A. ![]()
B. ![]()
C. ![]()
D. ![]()
Tìm m để Bất phương trình
4
sin
2
x
+
cos
2
x
+
17
sin
2
x
+
3
cos
2
x
+
m
+
1...
Đọc tiếp
Tìm m để Bất phương trình 4 sin 2 x + cos 2 x + 17 sin 2 x + 3 cos 2 x + m + 1 ≥ 2 luôn đúng?
![]()
![]()
![]()
![]()
Tìm m để Bất phương trình
4
sin
2
x
+
cos
2
x
+
17
sin
2
x
+
3
cos
2
x
+
m
+
1...
Đọc tiếp
Tìm m để Bất phương trình 4 sin 2 x + cos 2 x + 17 sin 2 x + 3 cos 2 x + m + 1 ≥ 2 luôn đúng ?
A. 10 - 1 ≤ m ≤ 15 + 29 2
B. 10 - 1 ≤ m ≤ 15 - 29 2
C. 10 - 3 ≤ m ≤ 15 - 29 2
D. 10 - 1 ≤ m ≤ 10 + 1
Tìm m để các bất phương trình sau đúng với mọi x
3
sin
2
x
+
cos
2
x
sin
2
x
+
4
cos
2
x
+...
Đọc tiếp
Tìm m để các bất phương trình sau đúng với mọi x
3 sin 2 x + cos 2 x sin 2 x + 4 cos 2 x + 1 ≤ m + 1
A. m = 1
B. m > 1
C. m > 2
D.Tất cả sai
Cho hệ bất phương trình \(\hept{\begin{cases}\frac{2x-17}{x-5}< 4\\\frac{x-2}{x-1}>2\end{cases}}\) có tập nghiệm \(\left(a;b\right)\).,Tìm m để bất phương trình \(m^2x+1\ge m+\left(3m-2\right)x\)có nghiệm đúng \(\forall x\in\left(a;b\right)\)
Giải nhanh hộ mình với ạ
Tìm tất cả các giá trị của m để bất phương trình
3
.
sin
2
x
+
cos
2
x
sin
2
x
+
4...
Đọc tiếp
Tìm tất cả các giá trị của m để bất phương trình 3 . sin 2 x + cos 2 x sin 2 x + 4 . cos 2 x + 1 ≤ m + 1 đúng với mọi x ∈ ℝ
![]()
![]()
![]()
![]()
1, cho phương trình sin2x-left(2m+sqrt{2}right)left(sinx+cosxright)+2msqrt{2}+10 tìm các giá trị m để phương trình có đúng 2 nghiệm xinleft(0;dfrac{5Pi}{4}right)2,tìm tất cả các giá trị thực của tham số m để phương trình cos2x+left(2m+1right)sinx-m-10 có đúng 2 nghiệm thuộc khoảng left(dfrac{Pi}{2};dfrac{3Pi}{2}right)3, cho phương trình cos^2x-2mcosx+6m-90 tìm các giá trị m để phương trình có nghiệm thuộc khoảng left(-dfrac{Pi}{2};dfrac{Pi}{2}right)
Đọc tiếp
1, cho phương trình \(sin2x-\left(2m+\sqrt{2}\right)\left(sinx+cosx\right)+2m\sqrt{2}+1=0\) tìm các giá trị m để phương trình có đúng 2 nghiệm \(x\in\left(0;\dfrac{5\Pi}{4}\right)\)
2,tìm tất cả các giá trị thực của tham số m để phương trình \(cos2x+\left(2m+1\right)sinx-m-1=0\) có đúng 2 nghiệm thuộc khoảng \(\left(\dfrac{\Pi}{2};\dfrac{3\Pi}{2}\right)\)
3, cho phương trình \(cos^2x-2mcosx+6m-9=0\) tìm các giá trị m để phương trình có nghiệm thuộc khoảng \(\left(-\dfrac{\Pi}{2};\dfrac{\Pi}{2}\right)\)