Cho \(\Delta ABC\) có \(\widehat{B}=30^0;\widehat{C}=20^0\).Trên cạnh BC lấy điểm của D sao cho BD=AC.Chứng minh rằng \(\Delta ADC\) cân tại D.
P/S:Một bài hình khá hay cho mọi người thưởng thức:)
Tuyển Cộng tác viên Hoc24 nhiệm kì 26 tại đây: https://forms.gle/dK3zGK3LHFrgvTkJ6
ZZ
Những câu hỏi liên quan
Cho \(\Delta ABC\) cân tại B , có \(\widehat{ABC}=80^o\) . Lấy điểm I nằm trong tam giác sao cho \(\widehat{IAC}=10^o\) và \(\widehat{ICA}=30^o\) . Tính số đo \(\widehat{AIB}\) .
Do ΔABC cân tại B => A = C = \(\dfrac{180^o-80^o}{2}=50^o\)
=> góc BAI = 50o - 10o = 40o
góc BCI = 50o - 30o = 20o
=> \(IBC=\dfrac{1}{3}ABI\Rightarrow IBC=\dfrac{80^o}{3+1}=20^o;ABI=80^o-20^o=60^o\)
\(\Leftrightarrow AIB=180^o-40^o-60^o=80^o\)
Đúng 2
Bình luận (0)
cho \(\Delta ABC\) vuông ở A. \(\widehat{B}-\widehat{C}=30^0\).Vẽ đường phân giác AD và đường cao AH của \(\Delta ABC\).Tính \(\widehat{HAD}\)
cho \(\Delta ABC\) có \(\widehat A={40^0}\) biết \(\widehat B= 3\widehat C\) tam giác abc là tam giác gì
giúp mik với
\(\widehat{B}+\widehat{C}=140^0\)
\(\Leftrightarrow4\cdot\widehat{C}=140^0\)
\(\Leftrightarrow\widehat{C}=35^0\)
hay \(\widehat{B}=105^0\)
Vậy: ΔABC tù
Đúng 0
Bình luận (0)
Tính các góc của \(\Delta ABC,\)biết \(\widehat{A}-\widehat{B}=45^0,\widehat{A}-\widehat{C}=30^0\)
mk lm đc bài này nhưng ko bt viết dấu
bạn ghi chữ cũng đc
Có:
góc A + góc B + góc C = 180 độ => góc B + góc C = 180 - góc A
Mà: góc A - góc B = 45 độ và góc A - góc C = 30 độ
=> CỘNG LẠI: 2.góc A - (góc B + góc C) = 75 độ
=> 2. góc A - (180 - góc A) = 75 độ
=> 3.góc A - 180 = 75
=> 3.góc A = 255 độ
=> góc A = 85 độ.
=> góc B = 40 độ
VÀ: góc C = 55 độ.
Xem thêm câu trả lời
1) Cho ΔABC cân tại A, các đường phân giác AD và BE. Biết ADdfrac{BE}{2}.Tính các góc của ΔABC?
2) Cho ΔABC cân tại A, widehat{B}widehat{C}50^0. Lấy điểm K nằm trong ΔABC sao cho widehat{KBC}10^0;widehat{KCB}30^0.
a, CM: ΔABK cân.
b, Tính widehat{BAK}?
3) Cho ΔABC có đường cao AHleft(AHperp BCright) và đường phân giác BD. Biết widehat{AHD}45^0. Tính widehat{ADB}?
Giải giúp mình nhé! Nhanh lên!!!!!!!!!!!!!!!!!!!!!!!!
Đọc tiếp
1) Cho ΔABC cân tại A, các đường phân giác AD và BE. Biết \(AD=\dfrac{BE}{2}\).Tính các góc của ΔABC?
2) Cho ΔABC cân tại A, \(\widehat{B}=\widehat{C}=50^0\). Lấy điểm K nằm trong ΔABC sao cho \(\widehat{KBC}=10^0;\widehat{KCB}=30^0\).
a, CM: ΔABK cân.
b, Tính \(\widehat{BAK}\)?
3) Cho ΔABC có đường cao AH\(\left(AH\perp BC\right)\) và đường phân giác BD. Biết \(\widehat{AHD}=45^0\). Tính \(\widehat{ADB}?\)
Giải giúp mình nhé! Nhanh lên!!!!!!!!!!!!!!!!!!!!!!!!
a. Cho \(\Delta AHBcó\widehat{H}=90^0,\widehat{BAH}=30^0\). Chứng minh BH = AB :2
b. Cho \(\Delta ABH\)có \(\widehat{B}=60^0\)và BA =2BH. Chứng minh \(\Delta ABH\)vuông.
Cho \(\Delta\)ABC có \(\widehat{B}\) = 300, 2AC = BC. CMR: \(\Delta\)ABC vuông tại A
Cho ΔABC có\(\widehat{B}=20,\widehat{C}=30\) , BC=60mm.tính diện tích ΔABC
Kẻ đường cao BH ⊥ AC tại H
Tam giác ABC có \(\widehat{A}+\widehat{B}+\widehat{C}=180^o\)
=> \(\widehat{A}=180^o-20^o-30^o=130^o\)
Xét tam giác BHC vuông tại H có :
+) sin C = \(\frac{BH}{BC}\) <=> BH = \(BC.\sin30^o\) = 30 mm
+) cos C = \(\frac{CH}{BC}\) <=> CH = \(BC.\cos30^o\) = \(30\sqrt{3}\) mm
Vì \(\widehat{BAC}+\widehat{BAH}=180^o\)
mà \(\widehat{BAC}=130^o\)
=> \(\widehat{BAH}=50^o\)
Xét tam giác ABH vuông tại H có :
tan A = \(\frac{BH}{AH}\) <=> AH = \(30\div\tan50^o\) \(\approx\) 25 mm
=> AC = HC - AH = \(30\sqrt{3}\) - 25 \(\approx\) 27 mm
=> \(S_{ABC}=\) \(\frac{BH.AC}{2}\) = 405 \(mm^2\)
Cho Hình 4.20, biết \(AB = CB, AD = CD,\widehat{DAB} = {90^\circ },\widehat{BDC} = {30^\circ }\)
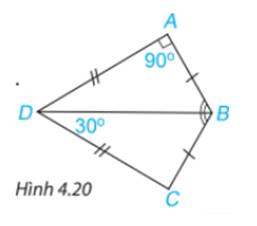
a) Chứng minh rằng \(\Delta ABD = \Delta CBD\).
b) Tính \(\widehat {ABC}\).
a) Xét \(\Delta ABD\) và \(\Delta CBD\)có:
DA=DC(gt)
BD chung
BA=BC
Vậy \(\Delta ABD = \Delta CBD\)(c.c.c)
b) Ta có \(\widehat A = \widehat C = {90^o}\)(hai góc tương ứng)
Theo định lí tổng ba góc trong tam giác BCD, ta có:
\(\begin{array}{l}\widehat C + \widehat {CDB} + \widehat {DBC} = {180^o}\\ \Rightarrow {90^o} + {30^o} + \widehat {DBC} = {180^o}\\ \Rightarrow \widehat {DBC} = {60^o}\end{array}\)
Mà \(\Delta ABD = \Delta CBD\) nên \(\widehat {ABD} = \widehat {CBD}\) ( 2 góc tương ứng)
\(\Rightarrow \widehat {ABD} = \widehat {CBD} = {60^o}\\\Rightarrow \widehat {ABC} = \widehat {ABD} + \widehat {CBD} = {60^o} + {60^o} = {120^o}\)
Đúng 1
Bình luận (0)