Cho a + b + c = 2p. Chứng minh đẳng thức
2bc + b2 + c2 - a2 = 4p( p- a)
Chứng minh đẳng thức :
a)(x-a)(x-b)+(x-b)(x-c)+(x-c)(x-a)=ab+bc+ca-x2 .Biết 2x=a+b+c
b)2bc+b2+c2-a2=4p(p-a) .Biết a+b+c=2p
bài 2: cho a+b+c=2p . chứng minh đẳng thức 2bc+b2+c2-a2+4p(p-a)
giúp mình với
mình đang rất cần gấp
#)Giải :
Ta có : \(a+b+c=2p\)
\(\Rightarrow b+c=2p-a\)
\(\Rightarrow\left(b+c\right)^2=\left(2p-a\right)^2\)
\(\Rightarrow b^2+c^2+2bc=4p^2-4pa+a^2\)
\(\Rightarrow2bc+b^2+c^2-a^2=4p\left(p-a\right)\)
\(\Rightarrowđpcm\)
\(Chứng minh các bất đẳng thức: a) (a + b)2 ≤ 2(a2 + b2) b) (a + b + c)2 ≤ 3(a2 + b2 + c2)\)
a)Ta có:
\(\left(a+b\right)^2+\left(a-b\right)^2=2\left(a^2+b^2\right)\)
Do \(\left(a-b\right)^2\ge0\),nên\(\left(a+b\right)^2\le2\left(a^2+b^2\right)\)
b)Xét \(\left(a+b+c\right)^2+\left(a-b\right)^2+\left(a-c\right)^2+\left(b-c\right)^2\)
Khai triển và rút gọn ta được:\(3\left(a^2+b^2+c^2\right)\)
Vậy \(\left(a+b+c\right)^2\le3\left(a^2+b^2+c^2\right)\)
a) Chứng minh : (ac + bd)2 + (ad bc)2 = (a2 + b2)(c2 + d2)
b) Chứng minh bất đẳng thức Bunhiacôpxki : (ac + bd)2 (a2 + b2)(c2 + d2)
a: \(VT=a^2c^2+2abcd+b^2d^2+a^2d^2-2abcd+b^2c^2\)
\(=a^2c^2+a^2d^2+b^2d^2+b^2c^2\)
\(=a^2\left(c^2+d^2\right)+b^2\left(c^2+d^2\right)\)
\(=\left(c^2+d^2\right)\left(a^2+b^2\right)\)
b: Bạn ghi lại đề đi bạn
10. Chứng minh các bất đẳng thức :
a) (a + b)2 ≤ 2(a2 + b2)
b) (a + b + c)2 ≤ 3(a2 + b2 + c2)
10. a) Ta có : (a + b)2 + (a – b)2 = 2(a2 + b2). Do (a – b)\(^2\) ≥ 0, nên (a + b)\(^2\) ≤ 2(a2 + b2).
b) Xét : (a + b + c)\(^2\) + (a – b)\(^2\) + (a – c)\(^2\) + (b – c)\(^2\)
. Khai triển và rút gọn, ta được : 3(a\(^2\) + b\(^2\) + c\(^2\)).
Vậy : (a + b + c)\(^2\) ≤ 3( a\(^2\) + b\(^2\) + c\(^2\)).
Cách khác : Biến đổi tương đương
a, \(\left(a+b\right)^2\le2\left(a^2+b^2\right)\)
\(\Leftrightarrow a^2+2ab+b^2\le2a^2+2b^2\)
\(\Leftrightarrow a^2-2ab+b^2\ge0\)
\(\Leftrightarrow\left(a-b\right)^2\ge0\)luôn đúng
b, \(\left(a+b+c\right)^2\le3\left(a^2+b^2+c^2\right)\)
\(\Leftrightarrow a^2+b^2+c^2+2ab+2ac+2bc\le3a^2+3b^2+3c^2\)
\(\Leftrightarrow2a^2+2b^2+2c^2-2ab-2bc-2ca\ge0\)
\(\Leftrightarrow\left(a-b\right)^2+\left(b-c\right)^2+\left(c-a\right)^2\ge0\)(Luôn đúng)
Câu 29. Chứng minh các bất đẳng thức:
a) (a + b)2 ≤ 2(a2 + b2)
b) (a + b + c)2 ≤ 3(a2 + b2 + c2)
c) (a1 + a2 + ….. + an)2 ≤ n(a12 + a22 + ….. + an2).
Câu 30. Cho a3 + b3 = 2. Chứng minh rằng a + b ≤ 2.
Câu 31. Chứng minh rằng: [x] + [y] ≤ [x + y].
Câu 32. Tìm giá trị lớn nhất của biểu thức: ![]()
Câu 33. Tìm giá trị nhỏ nhất của: ![]() với x, y, z > 0.
với x, y, z > 0.
Câu 36. Xét xem các số a và b có thể là số vô tỉ không nếu:
a) ab và a/b là số vô tỉ.
b) a + b và a/b là số hữu tỉ (a + b ≠ 0)
c) a + b, a2 và b2 là số hữu tỉ (a + b ≠ 0)
Câu 37. Cho a, b, c > 0. Chứng minh: a3 + b3 + abc ≥ ab(a + b + c)
Câu 38. Cho a, b, c, d > 0. Chứng minh:
![]()
Câu 39. Chứng minh rằng [2x] bằng 2[x] hoặc 2[x] + 1
Câu 40. Cho số nguyên dương a. Xét các số có dạng: a + 15 ; a + 30 ; a + 45 ; … ; a + 15n. Chứng minh rằng trong các số đó, tồn tại hai số mà hai chữ số đầu tiên là 96.
Câu 41. Tìm các giá trị của x để các biểu thức sau có nghĩa:
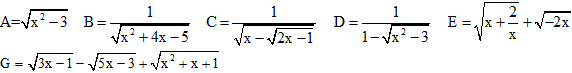 Mn giúp em với ;-;
Mn giúp em với ;-;
Cho a2+b2+c2=2p
a) a2-b2-c2+2bc=4(p-b)(p-c)
p2+(p-a)2+(p-b)2+(p-c)2=a2+b2+c2
2 là số mũ
Chứng minh các bất đẳng thức:
a) (a + b)2 ≤ 2(a2 + b2)
b) (a + b + c)2 ≤ 3(a2 + b2 + c2)
em chi moi hoc lop 5 thoi a
ma oi nhe
thì lấy về phải pt a)keo 2 ra ngoai
b)keo 3 ra ngoai
thì ta sẽ có điều cần chứng minh
còn = thì khi ẩn = 0
Cho a,b,c∈Ra,b,c∈R và a2+b2+c2=21a2+b2+c2=21. Chứng minh rằng: 7≤|a−2b|+|b−2c|+|c−2a|≤√3997≤|a−2b|+|b−2c|+|c−2a|≤399 Ý tưởng: ( Nhưng không chắc chắn là đúng hướng :'> ) Dùng bất đẳng thức Cauchy-Schwarz để chứng minh bài toán -> x1+x2+...+xn≤|x1|+|x2|+...+|xn|≤√n(x21+x22+...+x2n)
Bài 1: a) Chứng minh: (ac+bd)2+(ad-bc)2=(a2+b2)(c2+d2)
b) Chứng minh bất đẳng thức Bunhiacoopxki(ac+bd)2\(\le\) (a2+b2)(c2+d2)
Help me !!!!!!!!!!!
Bài 1:
Biến đổi tương đương thôi:
\((ac+bd)^2+(ad-bc)^2=a^2c^2+b^2d^2+2abcd+a^2d^2+b^2c^2-2abcd\)
\(=a^2c^2+b^2d^2+a^2d^2+b^2c^2=(a^2+b^2)(c^2+d^2)\)
Ta có đpcm
Bài 2: Áp dụng kết quả bài 1:
\((a^2+b^2)(c^2+d^2)=(ac+bd)^2+(ad-bc)^2\geq (ac+bd)^2\) do \((ad-bc)^2\geq 0\)
Dấu bằng xảy ra khi \(ad=bc\Leftrightarrow \frac{a}{c}=\frac{b}{d}\)