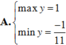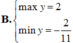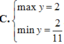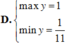Tìm GTLN-GTNN
y=2cosxcos3x+√3 sin4x-cosx+5
Tìm GTLN, GTNN của hàm số y = √(1−2sinx)
Giải phương trình lượng giác
a) sin4x + cos4x + sin4x = 1
b) tan2x + cotx = 4cos2x
Tìm GTLN và GTNN của hàm số y = sin x + 2 cos x + 1 sin x + cos x + 3 (*)
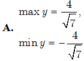
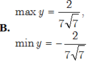


tìm gtln và gtnn của hàm số
a) y = sinxcox + 1
b) \(y=\sqrt{3}sinx-cosx-2\)
a.
\(y=sinx.cosx+1=\dfrac{1}{2}sin2x+1\)
\(-1\le sin2x\le1\Rightarrow\dfrac{1}{2}\le y\le\dfrac{3}{2}\)
\(y_{min}=\dfrac{1}{2}\) khi \(sin2x=-1\Rightarrow x=-\dfrac{\pi}{4}+k\pi\)
\(y_{max}=\dfrac{3}{2}\) khi \(sin2x=1\Rightarrow x=\dfrac{\pi}{4}+k\pi\)
b.
\(y=2\left(\dfrac{\sqrt{3}}{2}sinx-\dfrac{1}{2}cosx\right)-2=2.sin\left(x-\dfrac{\pi}{6}\right)-2\)
\(-1\le sin\left(x-\dfrac{\pi}{6}\right)\le1\Rightarrow-4\le y\le0\)
\(y_{min}=-4\) khi \(sin\left(x-\dfrac{\pi}{6}\right)=-1\Rightarrow x=-\dfrac{\pi}{3}+k2\pi\)
\(y_{max}=0\) khi \(sin\left(x-\dfrac{\pi}{6}\right)=1\Rightarrow x=\dfrac{2\pi}{3}+k2\pi\)
tìm GTLN, GTNN của hàm số
a/ y=1-2sinx
b/ y=cosx-\sqrt(3)\sin x+2021
a) \(y=1-2sinx\)
Ta có: \(-1\le sinx\le1\Rightarrow-2\le2sinx\le2\)
\(\Rightarrow2\ge-2sin2x\ge-2\)
\(\Rightarrow3\ge1-2sinx\ge-1\)
Vậy \(y_{max}=3,y_{min}=-1\)
Tìm GTLN và GTNN của y=cos2x+cosx
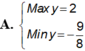
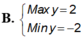

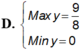
tìm GTLN - GTNN của hàm số : y=sinx+cosx+sinxcosx
Đặt \(sinx+cosx=t\Rightarrow-\sqrt{2}\le t\le\sqrt{2}\)
\(t^2=sin^2x+cos^2x+2sinx.cosx=1+2sinx.cosx\Rightarrow sinx.cosx=\dfrac{t^2-1}{2}\)
\(\Rightarrow y=t+\dfrac{t^2-1}{2}=\dfrac{1}{2}t^2+t-\dfrac{1}{2}\)
Xét hàm \(f\left(t\right)=\dfrac{1}{2}t^2+t-\dfrac{1}{2}\) trên \(\left[-\sqrt{2};\sqrt{2}\right]\)
\(-\dfrac{b}{2a}=-1\)
\(f\left(-\sqrt{2}\right)=\dfrac{1-2\sqrt{2}}{2}\) ; \(f\left(-1\right)=-1\) ; \(f\left(\sqrt{2}\right)=\dfrac{1+2\sqrt{2}}{2}\)
\(\Rightarrow y_{min}=-1\) khi \(t=-1\) ; \(y_{max}=\dfrac{1+2\sqrt{2}}{2}\) khi \(t=\sqrt{2}\)
Đặt \(t=sinx+cosx;t\in\left[-\sqrt{2};\sqrt{2}\right]\)
\(\Rightarrow\dfrac{t^2-1}{2}=sinx.cosx\)
\(y=t+\dfrac{t^2-1}{2}=\dfrac{t^2}{2}+t-\dfrac{1}{2}\)
Vẽ BBT của \(f\left(t\right)=\dfrac{t^2}{2}+t-\dfrac{1}{2};t\in\left[-\sqrt{2};\sqrt{2}\right]\)
\(\Rightarrow\)\(f\left(t\right)_{min}=-1\Leftrightarrow t=-1\Rightarrow sinx+cosx=-1\Leftrightarrow sin\left(x+\dfrac{\pi}{4}\right)=-\dfrac{1}{\sqrt{2}}\)....
\(f\left(t\right)_{max}=\dfrac{1+2\sqrt{2}}{2}\)\(\Leftrightarrow t=\sqrt{2}\Rightarrow sinx+cosx=\sqrt{2}\Leftrightarrow sin\left(x+\dfrac{\pi}{4}\right)=1\)....
Tìm GTLN, GTNN của \(y=\left|sinx\right|+\left|cosx\right|\)
tìm gtln và gtnn
y= căn 3 cos2x+2sinxcosx-2
y=căn3 cosx-sinx
\(y=\sqrt{3}cos2x+2sinxcosx-2\)
\(=\sqrt{3}cos2x+sin2x-2\)
Ta có: \(\left|\sqrt{3}cos2x+sin2x\right|\le\sqrt{\left(\sqrt{3}\right)^2+1^2}=2\)
Do đó \(-2\le\sqrt{3}cos2x+sin2x\le2\)
\(\Leftrightarrow-4\le\sqrt{3}cos2x+sin2x-2\le2\).
Ta có: \(\left|\sqrt{3}cosx-sinx\right|\le\sqrt{\left(\sqrt{3}\right)^2+\left(-1\right)^2}=2\)
Do đó \(-2\le\sqrt{3}cosx-sinx\le2\)
Tìm GTLN và GTNN của hàm số: y = 2 sin x + cos x + 3 2 cos x - sin x + 4