ƯCLN(60;165;315)
DN
Những câu hỏi liên quan
Đề bài: Tìm ƯCLN
a, ƯCLN ( 16, 24 )
b, ƯCLN ( 60, 90 )
c, ƯCLN ( 24, 84 )
d, ƯCLN ( 16, 60 )
e, ƯCLN ( 18, 77 )
g, ƯCLN ( 18, 90 )
h, ƯCLN ( 18, 30, 42 )
k, ƯCLN ( 26, 39, 48 )
a) ƯCLN ( 16, 24 )
16 = 23 24 = 22.3
ƯCLN ( 16;24 ) = 22= 4
b) ƯCLN ( 60, 90 )
60 = 22.3.5 90=2.32.5
ƯCLN ( 60;90 ) = 2.3.5 = 30
c) ƯCLN ( 24, 84 )
24 = 23.3 84 = 22.3.7
ƯCLN ( 24;84 ) = 22.3 = 12
d) ƯCLN ( 16, 60 )
16 = 24 60 = 22.3.5
ƯCLN ( 16;60 ) = 22=4
e) ƯCLN ( 18, 77 )
18 = 2.32 77=7.11
ƯCLN ( 18; 77 ) = 1
g) ƯCLN ( 18, 90 )
18 = 2.32 90=2.32.5
ƯCLN ( 18;90 ) = 2.32 = 18
h) ƯCLN ( 18, 30, 42 )
18 = 2.32 30 = 2.3.5 42 = 2.3.7
ƯCLN ( 18;30;42 ) = 2.3=6
k) ƯCLN ( 26, 39, 48 )
26 = 2.13 39 = 3.13 48 = 24.3
ƯCLN ( 26;39;48 ) = 1
Đúng 0
Bình luận (0)
Câu 5. Tìm ƯCLN(60 ; 90; 135)
Trả lời:
60 = …………
90 = ………….
135 = ……………
ƯCLN(60; 90; 135) = ……………………
Ta có:
60 = 2^2 .3.5; 90 = 2.3^2.5; 135 = 3^3 .5
<-> ƯCLN(60, 90, 135) = 3.5 = 15.
ƯC(60, 90, 135) = Ư(15) = {1, 3, 5, 15}
--thoT-T--
Đúng 2
Bình luận (0)
\(60=2^2.3.5\)
\(90=2.3^2.5\)
\(135=3^3.5\)
\(\Rightarrow ƯCLN(60;90;135)=3.5=15\)
Đúng 2
Bình luận (0)
Câu 3. Tìm ƯCLN và BCNN của 60; 80; 100
Trả lời:
60 = …………
80 = ………….
100 = ………….
ƯCLN(60; 80; 100) = ……………………
BCNN(60; 80; 100) = ……………………
\(60=2^2\cdot3\cdot5\)
\(80=2^4\cdot5\)
\(100=2^2\cdot5^2\)
\(ƯCLN\left(60;80;100\right)=2^2\cdot5=20\)
\(BCNN\left(60;80;100\right)=2^4\cdot3\cdot5^2=16\cdot3\cdot25=400\cdot3=1200\)
Đúng 1
Bình luận (0)
\(60=2^2.3.5\)
\(80=2^4.5\)
\(100=2^2.5^2\)
\(ƯCLN=2^2.5=20\)
\(BCNN=2^4.3.5^2=1200\)
Đúng 1
Bình luận (0)
a.Tìm ƯCLN và BCNN của 90; 120
b.Tìm ƯCLN và BCNN của 60; 144
c.Tìm ƯCLN; BCNN rồi tìm ước chung của 42; 35; 180
d.Tìm ƯCLN; BCNN rồi tìm bội chung của 48; 60; 72
a: UCLN=30
BCNN=360
b: UCLN=12
BCNN=720
Đúng 0
Bình luận (0)
Tìm ƯCLN(24, 60); ƯCLN(14, 33); ƯCLN(90, 135, 270).
+) 24 = 23.3
60 = 22.3.5
Ta thấy 2 và 3 là các thừa số nguyên tố chung. Số mũ nhỏ nhất của 2 là 2, số mũ nhỏ nhất của 3 là 1
=> ƯCLN(24, 60) = 22. 3 = 12.
+) 14 = 2.7
33 = 3.11
=> ƯCLN(14, 33) = 1
+) 90 = 2.32.5
135 = 33.5
270 = 2.33.5
Ta thấy 3 và 5 là các thừa số nguyên tố chung. Số mũ nhỏ nhất của 3 là 2, số mũ nhỏ nhất của 5 là 1
=> ƯCLN(90, 135, 270) = 32. 5 = 45.
Đúng 0
Bình luận (0)
8. Tìm:
a) ƯCLN (24; 108)
b) ƯCLN (60; 72)
c) ƯCLN (96; 192)
d) ƯCLN (24; 36; 160)
a: UCLN(24;108)=12
b: UCLN(60;72)=12
c: UCLN(96;192)=96
d: UCLN(24;36;160)=4
Đúng 3
Bình luận (0)
8. Tìm:
a) ƯCLN (24; 108)
b) ƯCLN (60; 72)
c) ƯCLN (96; 192)
d) ƯCLN (24; 36; 160)
\(a,24=2^3\cdot3;108=2^2\cdot3^3\\ \RightarrowƯCLN\left(24,108\right)=2^2\cdot3=12\\ b,60=2^2\cdot3\cdot5;72=2^3\cdot3^2\\ \RightarrowƯCLN\left(60,72\right)=2^2\cdot3=12\\ c,96=2^5\cdot3;192=2^6\cdot3\\ \RightarrowƯCLN\left(96,192\right)=2^5\cdot3=96\\ d,24=2^3\cdot3;36=2^2\cdot3^2;160=2^5\cdot5\\ \RightarrowƯCLN\left(24,36,160\right)=2^2=4\)
Đúng 2
Bình luận (0)
a,24=23⋅3;108=22⋅33⇒ƯCLN(24,108)=22⋅3=12b,60=22⋅3⋅5;72=23⋅32⇒ƯCLN(60,72)=22⋅3=12c,96=25⋅3;192=26⋅3⇒ƯCLN(96,192)=25⋅3=96d,24=23⋅3;36=22⋅32;160=25⋅5⇒ƯCLN(24,36,160)=22=4
Đúng 0
Bình luận (0)
a) ƯCLN(12,15, 28)
b) ƯCLN(15, 30, 60).
Tìm ƯC(36, 48), rồi tìm ƯCLN(36, 48).
Tìm:
a) ƯCLN(12,15, 28)
b) ƯCLN(15, 30, 60).
Tìm ƯCLN(18, 60)?
A. 6
B. 30
C. 12
D. 18
Đáp án là A
Ta có: 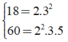
Nên ƯCLN(18; 60) = 2.3 = 6
Đúng 0
Bình luận (0)








